本文主要是介绍CLIP微调方法总结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 前言
- 1️⃣ Tip-Adapter
- 论文和源码
- 原理介绍
- 2️⃣Cross-modal Adaptation(跨模态适应)
- 论文和源码
- 原理介绍
- 3️⃣ FD-Align(Feature Discrimination Alignment,特征判别对齐)
- 论文和源码
- 原理介绍
- 总结
前言

本文主要介绍和总结了三种不错的 C L I P CLIP CLIP微调方法,包括原理和思想,并且按照自己的理解给出了相应的代码实现,相当于是一个简化版的code实现。
所有代码使用 j i t t o r jittor jittor框架实现,具体代码请请参考👇
Gitlink-Code 或者 Github-Code
1️⃣ Tip-Adapter
论文和源码
🔥 论文地址
🚀 代码地址
原理介绍
-
本质上就是在 C L I P CLIP CLIP的预测结果 X X X上又加上了一个预测结果 Y Y Y,我们都知道结果 X X X是测试图像和所有分类文本的相似度之间的关系,而 Y Y Y就是测试图像和训练 C L I P CLIP CLIP时的训练图像之间的相似度关系,最终将 X X X和 Y Y Y加权求和便得到最终的预测结果,所以可以发现他的优势在于: Z e r o − s h o t t r a n s f e r (无需额外训练) Zero-shot\ transfer(无需额外训练 ) Zero−shot transfer(无需额外训练)
-
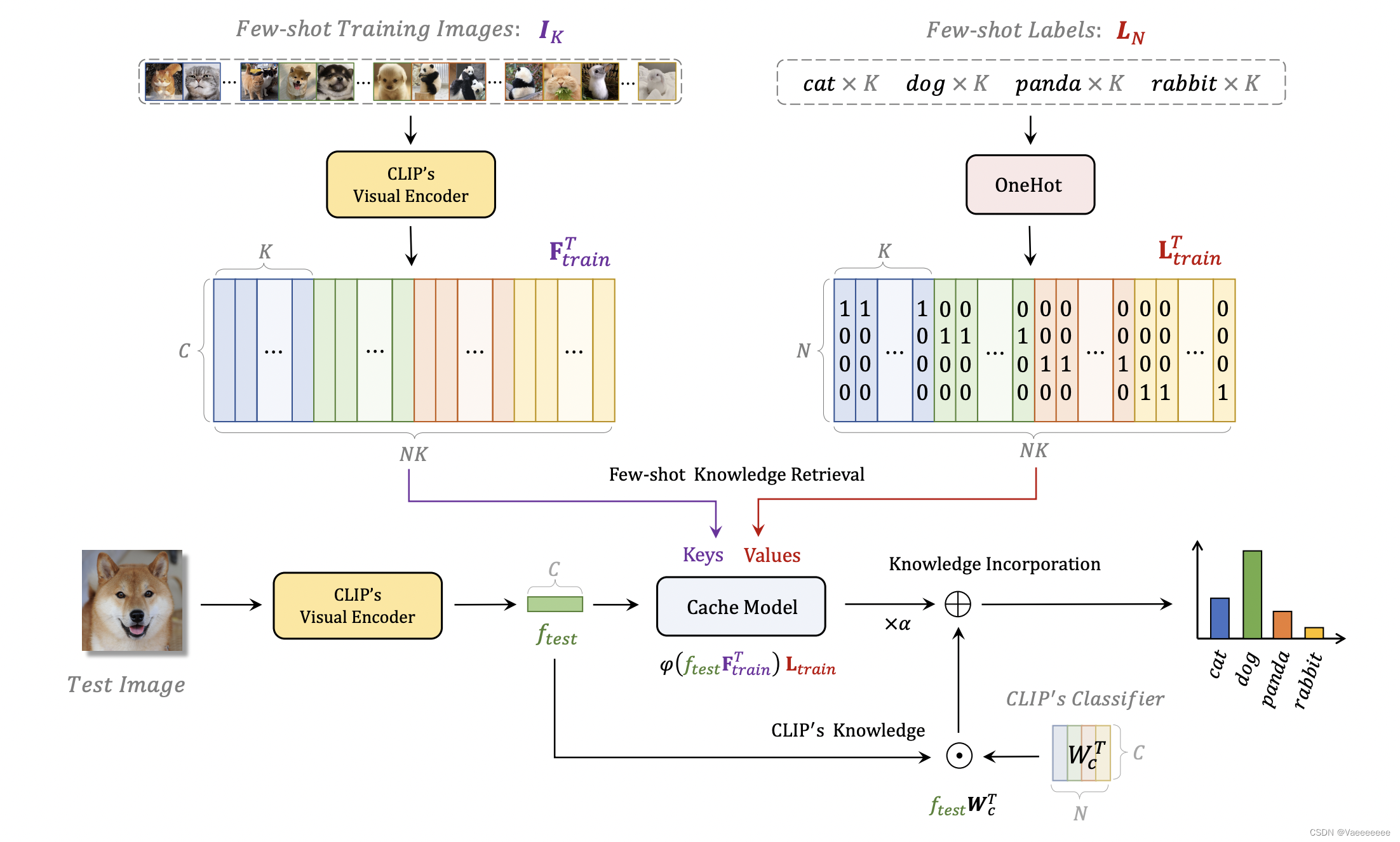
下面结合论文给的框架图就能很好理解这个方法(每个变量后面标出了 s h a p e shape shape大小,方便理解):
T i p − A d a p t e r Tip-Adapter Tip−Adapter添加之前:假设分类类别数目是 N N N, W c T W_{c}^{T} WcT是 N N N个文本标签经过 C L I P CLIP CLIP的 T e s t E n c o d e r Test\ Encoder Test Encoder得到的文本特征,大小 N × 512 N×512 N×512
输入一张测试图像 I t e s t I_{test} Itest → 经过 C L I P 模型的 V i s u a l E n c o d e r 之后 \xrightarrow{经过CLIP模型的Visual\ Encoder之后} 经过CLIP模型的Visual Encoder之后得到 f t e s t : 1 × 512 f_{test} :1×512 ftest:1×512 → 和 C L I P 的 T e s t F e a t u r e s 作相似度,也就是图中的 f t e s t ∗ W c T \xrightarrow{和CLIP的Test\ Features作相似度,也就是图中的f_{test}*W_{c}^{T}} 和CLIP的Test Features作相似度,也就是图中的ftest∗WcT得到分类结果(实际上就是和所有文本标签的相似度) X : 1 × N X:1×N X:1×NT i p − A d a p t e r Tip-Adapter Tip−Adapter添加之后:
上面步骤同样完全相同,得到 X X X;
首先将所有的训练图像 I K I_{K} IK(假设共有 M M M张, M = C × N M=C×N M=C×N, C C C是一个系数,因为训练时一般每个类别的图像会有多张) → 同样经过 C L I P 模型的 V i s u a l E n c o d e r \xrightarrow{同样经过CLIP模型的Visual\ Encoder} 同样经过CLIP模型的Visual Encoder得到 F t r a i n : M × 512 F_{train}:M×512 Ftrain:M×512 ,并作为缓存模型( c a c h e m o d e l cache\ model cache model)的 k e y key key
然后将所有训练图像的文本标签经过 O n e H o t One\ Hot One Hot处理,得到 L t r a i n : M × N L_{train}:M×N Ltrain:M×N,并作为缓存模型的 v a l u e value value;到此便构建了一个缓存模型,相当于多了一份存储有训练样本特征的先验信息。
接着将之前得到的 f t e s t : 1 × 512 f_{test} :1×512 ftest:1×512 → 送入 c a c h e m o d e l , 计算和训练图像之间的特征余弦相似度 \xrightarrow{送入cache\ model,计算和训练图像之间的特征余弦相似度} 送入cache model,计算和训练图像之间的特征余弦相似度得到 A = e x p ( − β ( 1 − f t e s t F t r a i n T ) ) : 1 × M A=exp(-\beta(1-f_{test}F_{train}^{T})):1×M A=exp(−β(1−ftestFtrainT)):1×M → 和 c a c h e m o d e l 的 v a l u e s 相乘,得到预测结果 Y \xrightarrow{和cache\ model的values相乘,得到预测结果Y} 和cache model的values相乘,得到预测结果Y Y = A L t r a i n : 1 × N Y=AL_{train}:1×N Y=ALtrain:1×N
最后将 T i p − A d a p t e r Tip-Adapter Tip−Adapter的预测结果 Y Y Y和原始 C L I P CLIP CLIP预测结果 X X X进行加权求和:
logits = α A L train + f test W c T = α φ ( f t e s t F t r a i n T ) L t r a i n + f t e s t W c T , \begin{aligned} \begin{aligned} \text{logits}& =\alpha A\mathbf{L}_\text{train}+f_\text{test}W_c^T \\ &=\alpha\varphi(f_{\mathrm{test}}\mathbf{F}_{\mathrm{train}}^T)\mathbf{L}_{\mathrm{train}}+f_{\mathrm{test}}W_c^T, \end{aligned} \end{aligned} logits=αALtrain+ftestWcT=αφ(ftestFtrainT)Ltrain+ftestWcT,
2️⃣Cross-modal Adaptation(跨模态适应)
论文和源码
🔥 论文地址
🚀 代码地址
原理介绍
- 原理图和伪代码
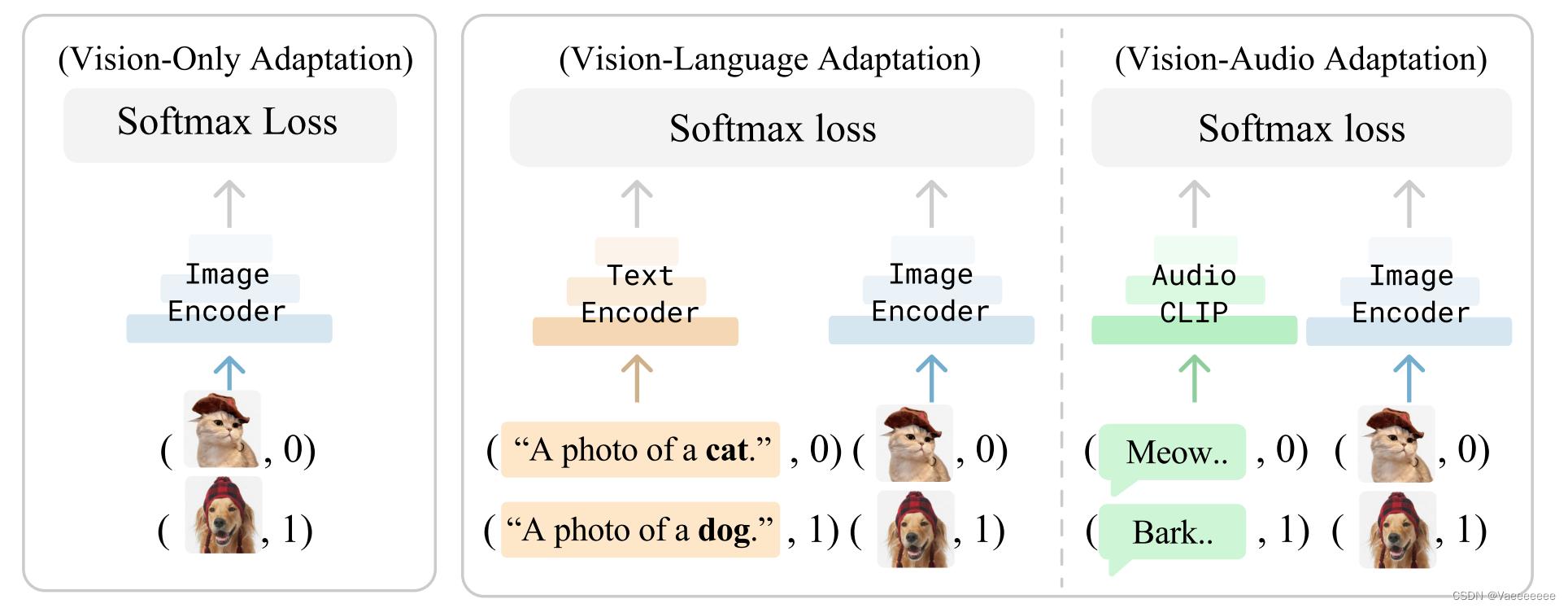

- 该方法的核心思想就是将多种模态的信息融合在一起,并且论文假设 C L I P CLIP CLIP可以将不同模态的样本映射到同一个特征空间。比如对于文本-图像这种模态形式,在训练过程中,就可以引入这里的文本信息(也就是每个类别的标签),将其作为额外的训练样本,其实就是将每张图像的图像特征和文本特征视作同一个特征来进行训练。
- 同上面一样,根据伪代码的内容,将维度变换显示出来也非常好理解整个实现过程:
假设输入的 b a t c h _ s i z e batch\_size batch_size大小为 b b b,分类的类别数为 n u m _ c l a s s num\_class num_class
i m a g e _ e n c o d e r 输出的图像特征 i m _ f : b × 512 t e x t _ e n c o d e r 输出的文本特征 t x _ f : b × 512 在行维度上将两个特征拼接起来并归一化 f e a t u r e s : 2 b × 512 对应的标签也进行拼接 l a b e l s : 2 b × 512 将 f e a t u r e s 通过一个分类器得到每个类别的预测概率 l o g i t s : 2 b × n u m _ c l a s s 最后 l o g i t s 和 l a b e l s 之间作交叉熵损失,并更新分类器、图像编码器和文本编码器的参数 \begin{aligned} image\_encoder输出的图像特征 \quad im\_f:b×512\\ text\_encoder输出的文本特征 \quad tx\_f:b×512\\ 在行维度上将两个特征拼接起来并归一化\quad features:2b×512\\ 对应的标签也进行拼接\quad labels:2b×512\\ 将features通过一个分类器得到每个类别的预测概率 \quad logits:2b×num\_class\\ 最后logits和labels之间作交叉熵损失,并更新分类器、图像编码器和文本编码器的参数 \end{aligned} image_encoder输出的图像特征im_f:b×512text_encoder输出的文本特征tx_f:b×512在行维度上将两个特征拼接起来并归一化features:2b×512对应的标签也进行拼接labels:2b×512将features通过一个分类器得到每个类别的预测概率logits:2b×num_class最后logits和labels之间作交叉熵损失,并更新分类器、图像编码器和文本编码器的参数
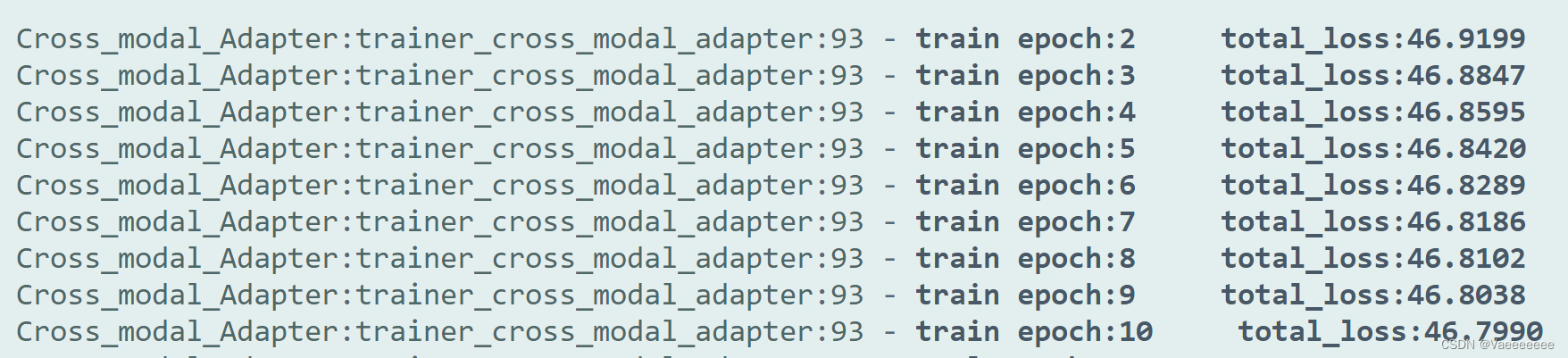
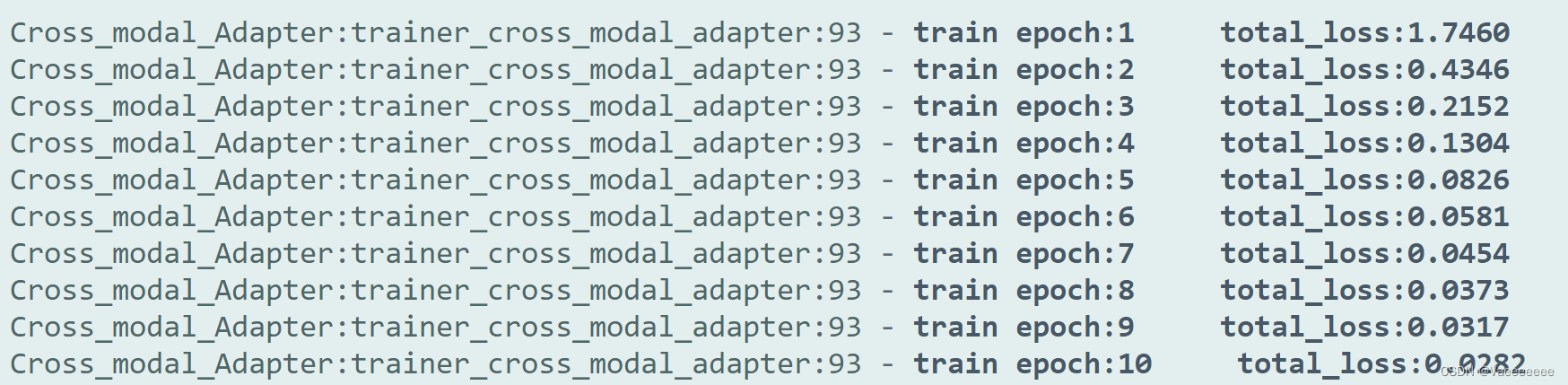
注意:在实现该代码进行训练的过程中发现如果按照伪代码中将cross_logits除以一个常量,loss反而会很难下降,相反乘上一个系数loss下降的更好一些。(直接loss=cross_entropy_loss(logits*3.0,labels)即可),否则loss值很难会下降。
3️⃣ FD-Align(Feature Discrimination Alignment,特征判别对齐)
论文和源码
🔥 论文地址
🚀 代码地址
原理介绍
- 原理图:
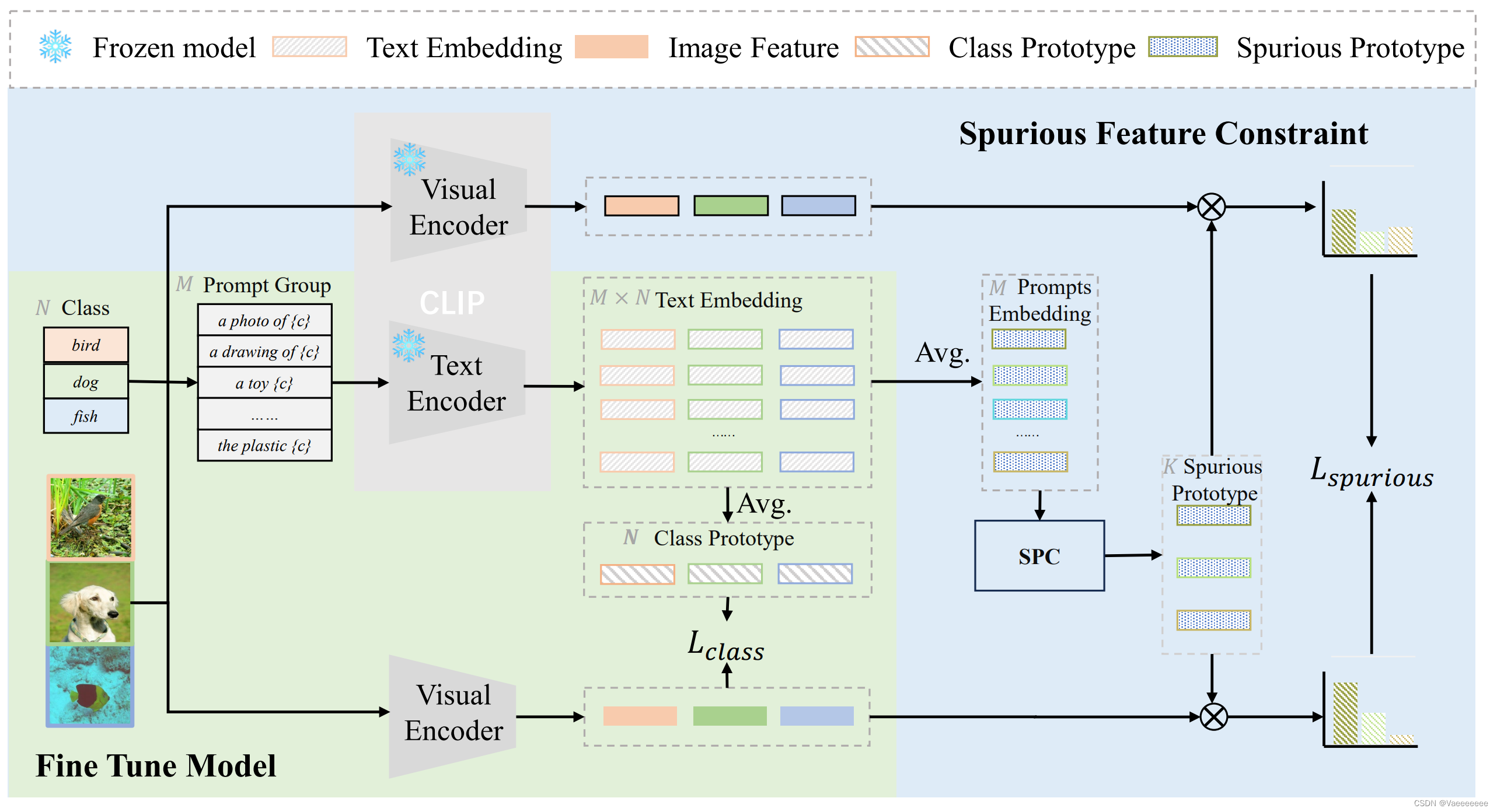
- 论文中提出了一个概念:虚假关联性的鲁棒性,它指的是模型是否具有区分出样本中和类别相关信息(因果信息)以及(背景、风格等)类别无关信息(虚假信息)的能力。同时注意到全微调的CLIP的OOD性能会下降,因此提出了一种不影响模型对虚假特征识别能力的微调方法来保证微调后的模型对虚假关联性的鲁棒性。从模型框架图中看,实际上就是在微调的过程中通过约束微调后的CLIP模型和原始的CLIP模型对虚假特征的分布保持一致,从而在一定程度上避免微调过程中CLIP的OOD性能下降。
- 该方法相对于前两个方法稍显复杂,先熟悉它定义的几个符号意义,再来结合框架图看一下它的整个模型原理:
首先假设存在一个小样本数据集 D ⊂ X × Y ,( X 表示图像, Y 表示标签) 有 M 个提示模板 ( P 1 , … , P M ) , C L I P 模型的 t e x t − e n c o d e r 和 i m a g e − e n c o d e r 分别表示为 g 0 和 f 0 ; 假设任意的一个类别 y ,那么 y 的原型表示为: μ y class ,也被称为类的原型 首先假设存在一个小样本数据集D\subset X\times Y,(X表示图像,Y表示标签)\\ 有M个提示模板(P_1,\ldots,P_M),CLIP模型的text-encoder和image-encoder分别表示为g_{0}和f_{0};\\ 假设任意的一个类别y,那么y的原型表示为:\mu_y^\text{class },也被称为类的原型 首先假设存在一个小样本数据集D⊂X×Y,(X表示图像,Y表示标签)有M个提示模板(P1,…,PM),CLIP模型的text−encoder和image−encoder分别表示为g0和f0;假设任意的一个类别y,那么y的原型表示为:μyclass ,也被称为类的原型
μ y class : = 1 M ∑ j = 1 M g 0 ( [ P j , y ] ) . \begin{aligned} \mu_y^\text{class }:=\frac{1}{M}\sum_{j=1}^Mg_0([P_j,y]). \end{aligned} μyclass :=M1j=1∑Mg0([Pj,y]).
因此第一个损失函数 L c l a s s \mathcal{L}_{\mathrm{class}} Lclass和clip模型中的损失函数本质上相同的,约束图像-文本之间的相似度,只不过这里的文本不在是单个的prompt,而是多个prompt取平均值得到的。
L class = − 1 ∣ D ∣ ∑ ( x i , y i ) ∈ D log exp ( s ( f t ( x i ) , μ y i class ) ) ∑ y ∈ Y exp ( s ( f t ( x i ) , μ y class ) ) 其中, s ( : ) 表示余弦相似度 \begin{aligned} \mathcal{L}_{\text{class}}=-\frac{1}{|\mathcal{D}|}\sum_{(x_i,y_i)\in\mathcal{D}}\log\frac{\exp(s(f_t(x_i),\mu_{y_i}^{\text{class}}))}{\sum_{y\in\mathcal{Y}}\exp(s(f_t(x_i),\mu_y^{\text{class}}))}\\ 其中,s(:)表示余弦相似度 \end{aligned} Lclass=−∣D∣1(xi,yi)∈D∑log∑y∈Yexp(s(ft(xi),μyclass))exp(s(ft(xi),μyiclass))其中,s(:)表示余弦相似度
紧接着,定义提示模板( p r o m p t )的原型:每个 P j 在所有类中的特征平均值,公式为: 紧接着,定义提示模板(prompt)的原型:每个P_{j}在所有类中的特征平均值,公式为: 紧接着,定义提示模板(prompt)的原型:每个Pj在所有类中的特征平均值,公式为:
μ P j spurious : = 1 ∣ Y ∣ ∑ y ∈ Y g 0 ( [ P j , y ] ) \begin{aligned} \mu_{P_j}^\text{spurious}:=\frac{1}{|\mathcal{Y}|}\sum_{y\in\mathcal{Y}}g_0([P_j,y]) \end{aligned} μPjspurious:=∣Y∣1y∈Y∑g0([Pj,y]) 现在希望的是在微调过程中保持模型对虚假相关性的鲁棒性 , 即保持模型在微调前后提取的虚假特征不变。 所以需要知道模型在虚假特征上的分布——即将微调模型提取的特征与虚假原型之间的相似度定义为模型虚假特征的分布。 现在希望的是在微调过程中保持模型对虚假相关性的鲁棒性,即保持模型在微调前后提取的虚假特征不变。\\所以需要知道模型在虚假特征上的分布——即将微调模型提取的特征与虚假原型之间的相似度定义为模型虚假特征的分布。 现在希望的是在微调过程中保持模型对虚假相关性的鲁棒性,即保持模型在微调前后提取的虚假特征不变。所以需要知道模型在虚假特征上的分布——即将微调模型提取的特征与虚假原型之间的相似度定义为模型虚假特征的分布。
因此,计算由微调模型提取的特征和虚假原型之间的相似性,并且如下产生虚假特征的分布: 因此,计算由微调模型提取的特征和虚假原型之间的相似性,并且如下产生虚假特征的分布: 因此,计算由微调模型提取的特征和虚假原型之间的相似性,并且如下产生虚假特征的分布:
P spurious ( x ; f t ) = SoftMax [ s ( f t ( x ) , μ P 1 spurious ) , … , s ( f t ( x ) , μ P M spurious ) ] \begin{aligned} \mathcal{P}_\text{spurious}(x;f_t)=\text{SoftMax}\left[s\left(f_t(x),\mu_{P_1}^\text{spurious}\right),\ldots,s\left(f_t(x),\mu_{P_M}^\text{spurious}\right)\right] \end{aligned} Pspurious(x;ft)=SoftMax[s(ft(x),μP1spurious),…,s(ft(x),μPMspurious)]
类似地,将 f t 换成 f 0 ,可以得到微调前模型的虚假特征分布: 类似地,将f_{t}换成f_{0},可以得到微调前模型的虚假特征分布: 类似地,将ft换成f0,可以得到微调前模型的虚假特征分布:
P spurious ( x ; f 0 ) = SoftMax [ s ( f 0 ( x ) , μ P 1 spurious ) , … , s ( f 0 ( x ) , μ P M spurious ) ] \begin{aligned} \mathcal{P}_{\text{spurious}}(x;f_0)=\text{SoftMax}\left[s\left(f_0(x),\mu_{P_1}^{\text{spurious}}\right),\ldots,s\left(f_0(x),\mu_{P_M}^{\text{spurious}}\right)\right] \end{aligned} Pspurious(x;f0)=SoftMax[s(f0(x),μP1spurious),…,s(f0(x),μPMspurious)]
因此第二个损失函数的作用就是保持微调前后模型对虚假特征概率分布保持一致:
L spurious = 1 ∣ D ∣ ∑ ( x i , y i ) ∈ D KL ( P spurious ( x i ; f t ) ∣ ∣ P spurious ( x i ; f 0 ) ) \begin{aligned} \mathcal{L}_{\text{spurious}}=\frac{1}{|\mathcal{D}|}\sum_{(x_i,y_i)\in\mathcal{D}}\text{KL}\left(\mathcal{P}_{\text{spurious}}(x_i;f_t)\mid\mid\mathcal{P}_{\text{spurious}}(x_i;f_0)\right) \end{aligned} Lspurious=∣D∣1(xi,yi)∈D∑KL(Pspurious(xi;ft)∣∣Pspurious(xi;f0))
综上,最终的损失函数为:
L t o t a l = α ⋅ L c l a s s + β ⋅ L s p u r i o u s 论文中取 α = 1 , β = 20 \begin{aligned} \mathcal{L}_{\mathrm{total}}=\alpha\cdot\mathcal{L}_{\mathrm{class}}+\beta\cdot\mathcal{L}_{\mathrm{spurious}} \end{aligned}\\ 论文中取\alpha=1,\beta=20 Ltotal=α⋅Lclass+β⋅Lspurious论文中取α=1,β=20
更多细节的推导和更准确的表述请参考作者的原论文😀
总结
- 本文介绍了三种CLIP微调方法的原理以及给出了对应的更加简化版代码实现,如果有问题的地方,欢迎评论区指正。
- 三种方法相比较而言,Tip-Adapter最通用,无论是免训练版本还是训练版本,使用之后均有一定的提升效果;Cross-modal Adaptation思路最简单,但是要想有效果,尝试后发现需要针对自己的数据集不断调节参数大小;FD-Align方法在保持CLIP的zero-shot能力方面是几个方法当中最好的;
- 觉得有帮助的话,给个赞吧👋👋👋
这篇关于CLIP微调方法总结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





