本文主要是介绍线性代数的本质(笔记三),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
点积与对偶性(Dot products and duality)
点积的运算
点积(点乘,数量积,内积)的标准方法:
两个维数相同的向量,将相应的坐标配对,求出每一对的乘积,然后相加即可。
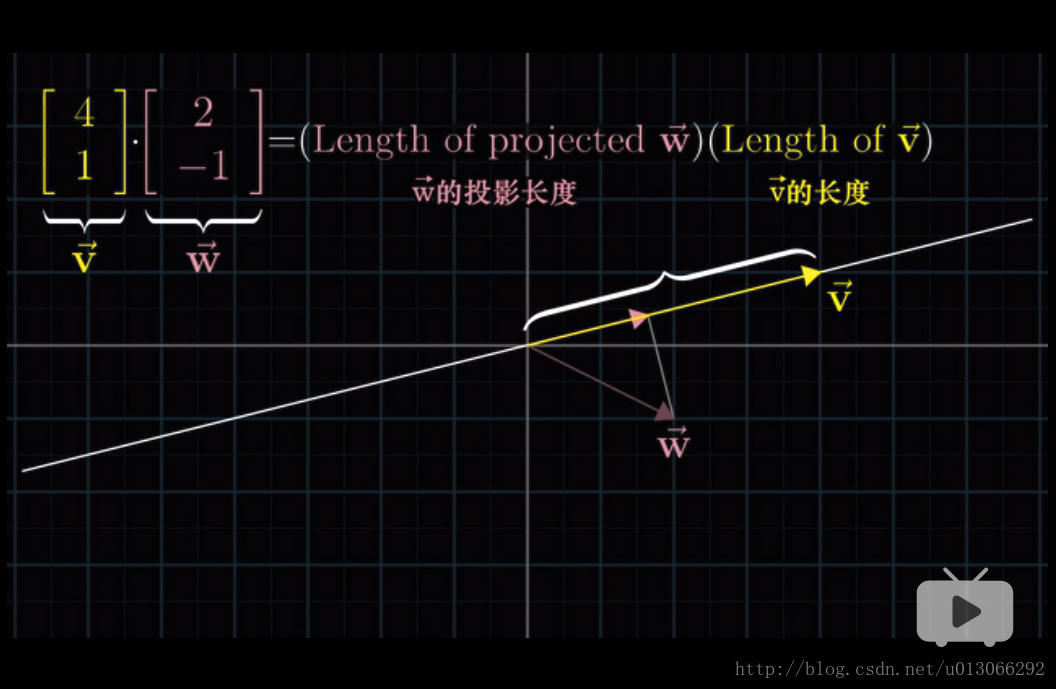
投影
在几何上的表现是一个向量在另一个向量上的 投影的长度 * 另一个向量的长度。
那么两者相乘的结果:
- >0 表示两个向量的方向在同一侧
- =0 表示两个向量垂直
- <0 表示两个向量的方向相反(不在同一侧)
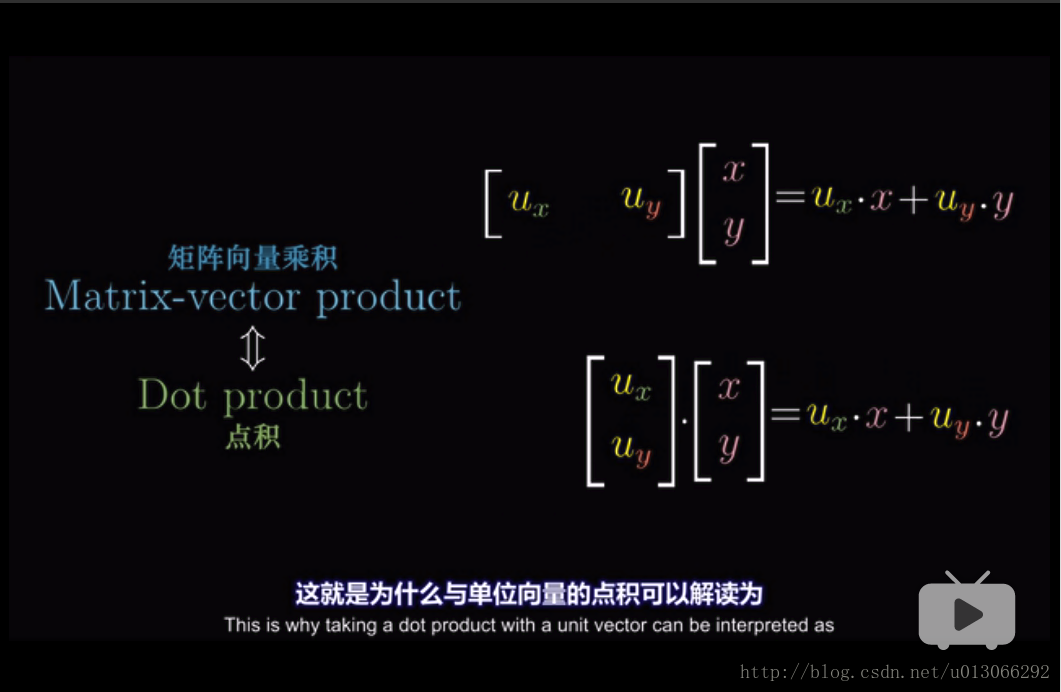
为什么点积的运算和投影有联系?
前言
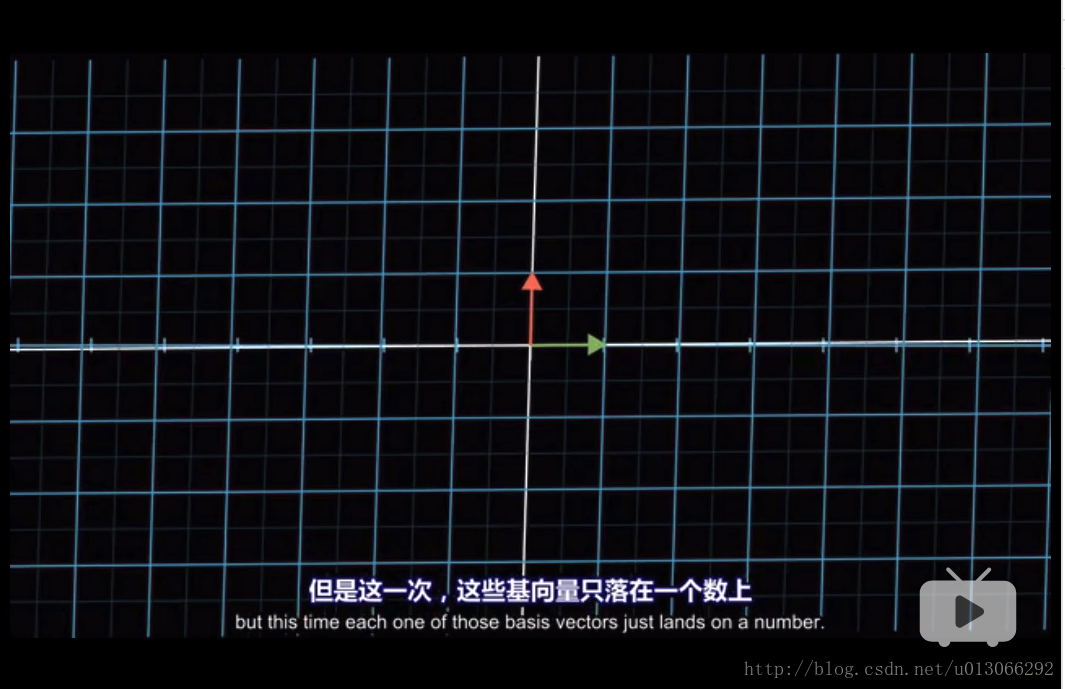
由于线性变换的约束,当一个多维上的等距分布的点降到一维的时候,这些点仍然符合等距分布,否则就不是线性变换。
举个例子:
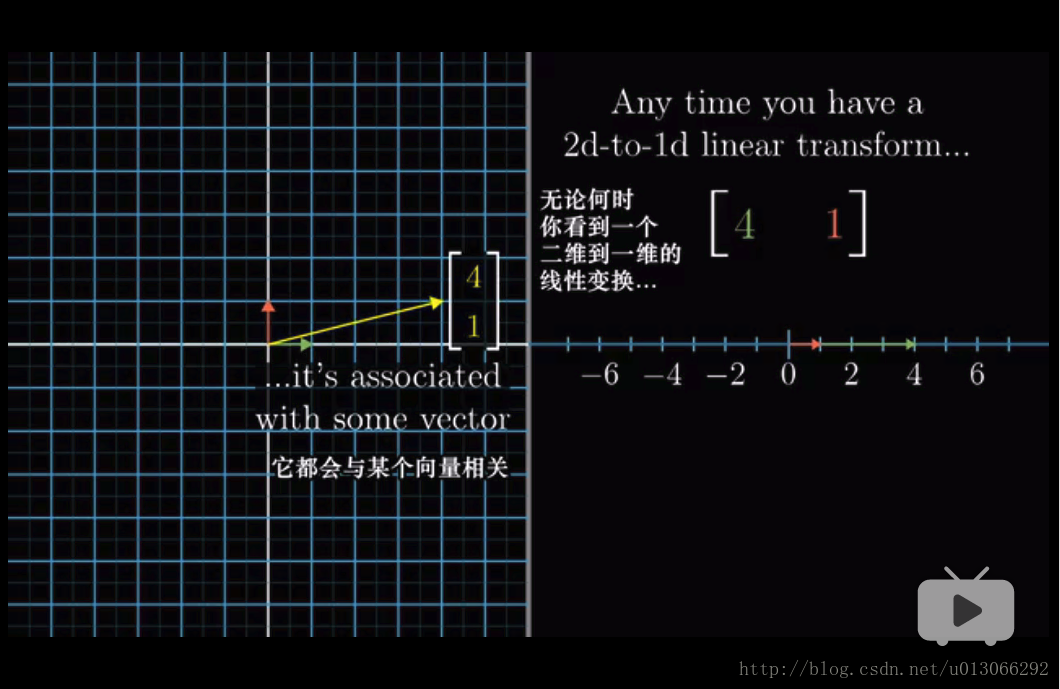
当一个二维向量变换成一维向量的时候,它原本向量的二维坐标就只能用一个坐标来表示:
那么我们要知道从二维到一维这个变换后原来任一向量改变后的结果,就如之前说的,只要先知道基向量的变换即可,然后进行线性组合得到该向量在变换后的一维里的位置。
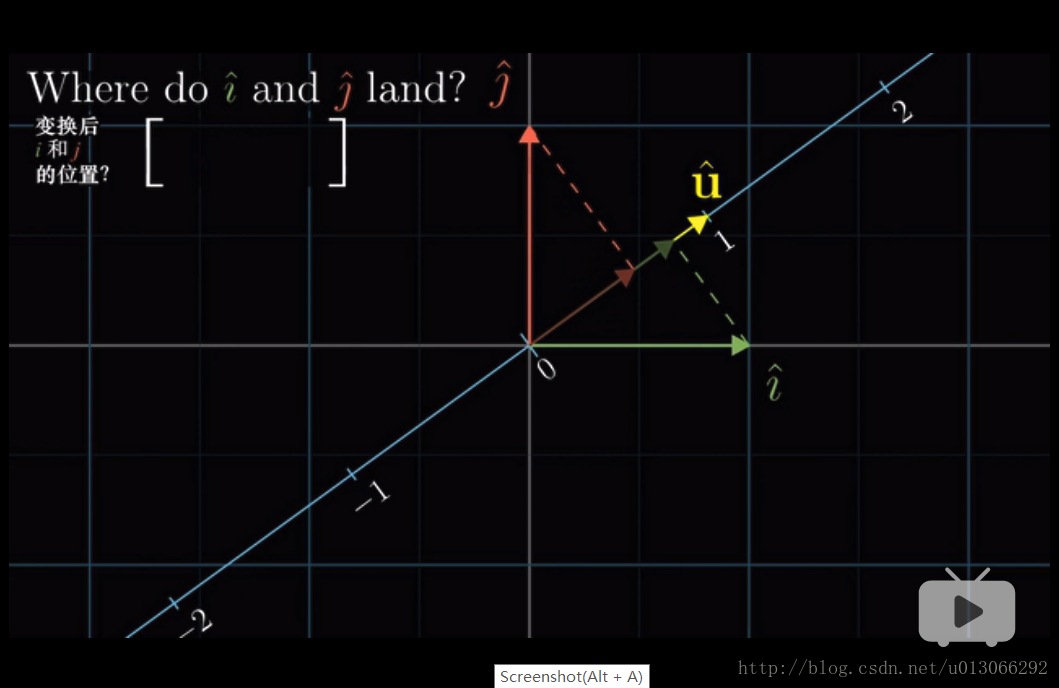
现在我们在一个二维的平面里放入一条数轴(一维),然后二维空间里有一个向量刚好落在数轴的坐标1上(也就是该向量在一维上是单位向量),我们想知道这个二维如果投影到一维上,会是怎样的?(就像一个立体的人的影子在地面上的话,人体上的点会是在地面上的哪个位置)
那么在这个问题上我们同样考虑基向量的变换,这样就能推出其它向量的变换。
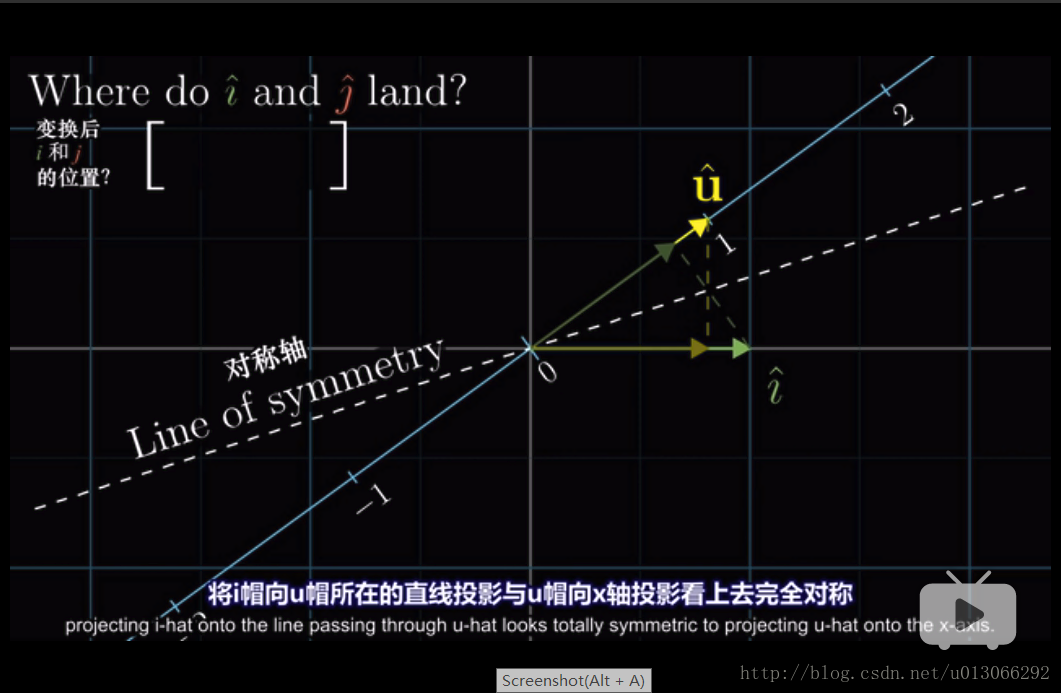
那么由于都是单位向量,即长度上都是1,那么利用对称性
u向量在i向量上的投影的长度,其实也就是i向量在u向量上投影的长度,这样就能知道i向量在一维上的位置;同理j向量也一样。也就是通过这种方法就可以知道二维里的两个基向量在一维上的位置。
那么也可以这样说,二维里i,j两个基向量在一维里的位置,其实就是一维里u在二维里的i和j上投影的位置。
对偶性(Duality)
这篇关于线性代数的本质(笔记三)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!