本文主要是介绍线性代数的本质(笔记二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
行列式
理解矩阵的行列式其实就是理解线性变换对“体积”的影响。
(在二维里,就是指面积变化前后的缩放比例;那么三维里就是体积变化前后的缩放比例。)
以三维为例:
- 当行列式的值>1时,就是体积被放大;
- 当行列式的值>0且<1时,就是体积被缩小;
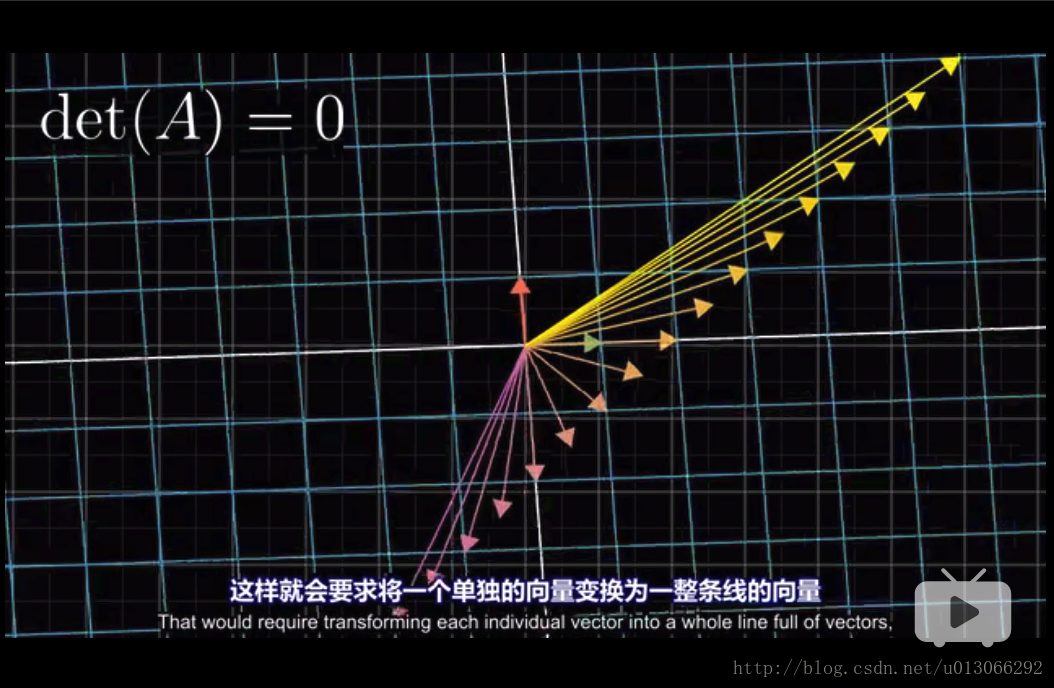
- 当行列式的值=0时,就是降维了,从立体(三维)变成了平面(二维);
- 当行列式的值<0时,就是翻转了,但绝对值还是表现缩放的比例。
扩展阅读 :行列式的本质
逆矩阵、列空间与零向量
逆矩阵(Inverse Matrices)
一个矩阵的行列式不等于0,则意味着它存在逆矩阵。
如果行列式为0,为什么没有逆矩阵呢?因为意味着逆后会有多种可能,也就是不唯一。
秩(Rank)
变换后空间的维数。
例如一个二维的空间最大的秩为2;三维的空间最大的秩为3。
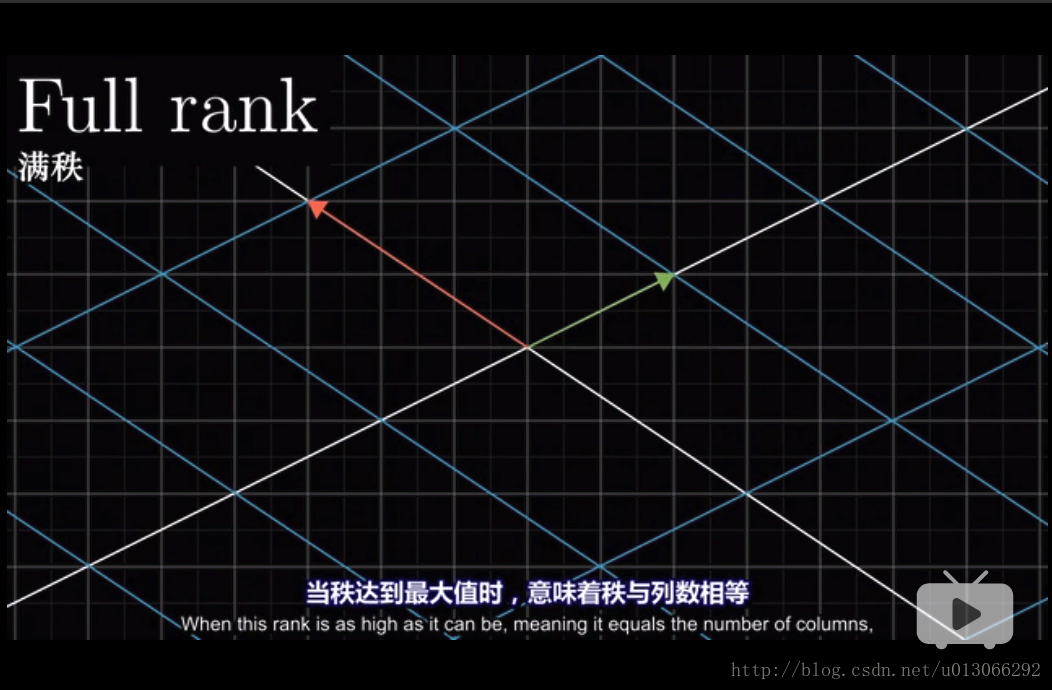
满秩(Full Rank)
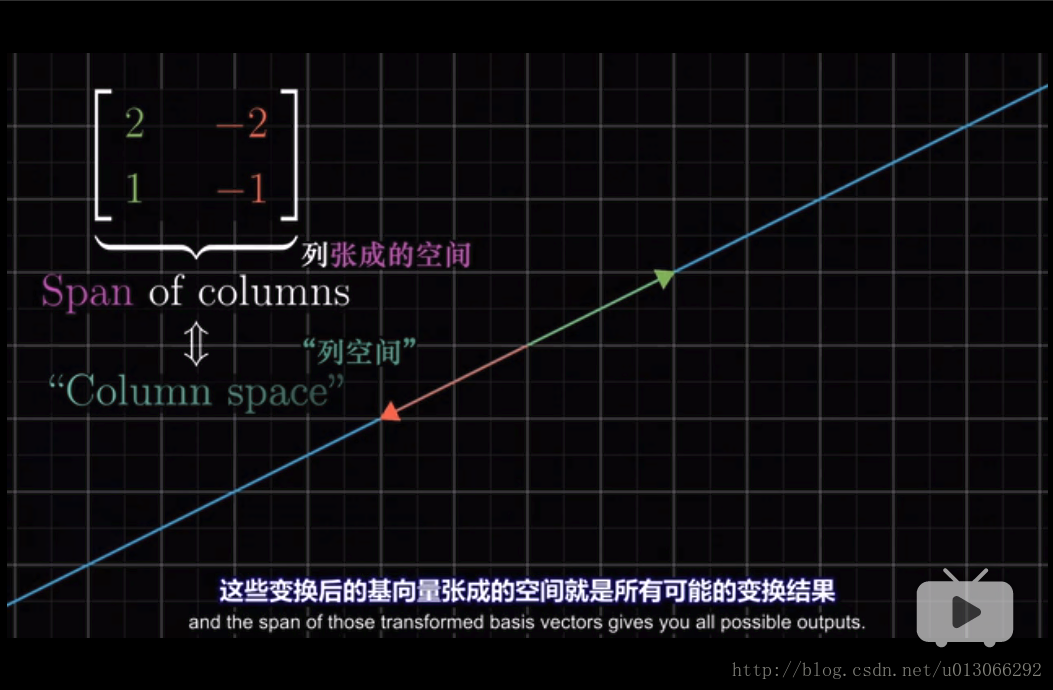
列空间(Column Space)
如何理解列空间?
零向量
对于满秩矩阵来说,只有零向量在变换后落在原点。(像原始三维里,也就零向量会落在原点。)
对于非满秩矩阵来说,意味着有一系列的向量在变换后称为零向量。(如果三维被变成了二维,就意味着有一维被压缩在原点里。)
零空间(null space)
变换后落在原点的向量的集合。
非方阵
非方阵就是它不是n*n的矩阵。
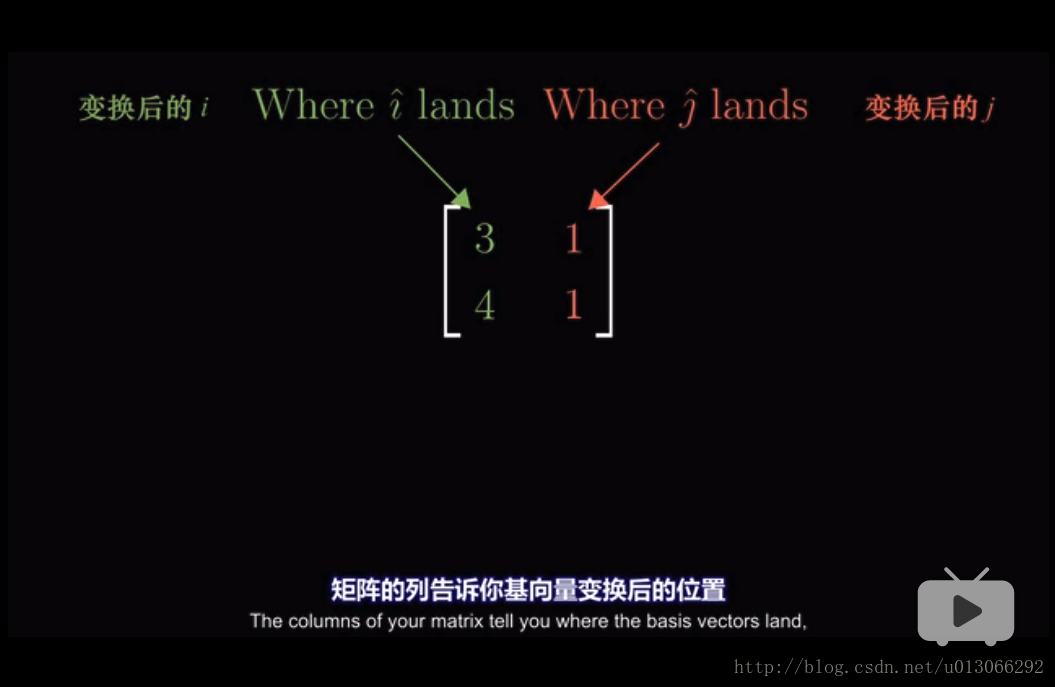
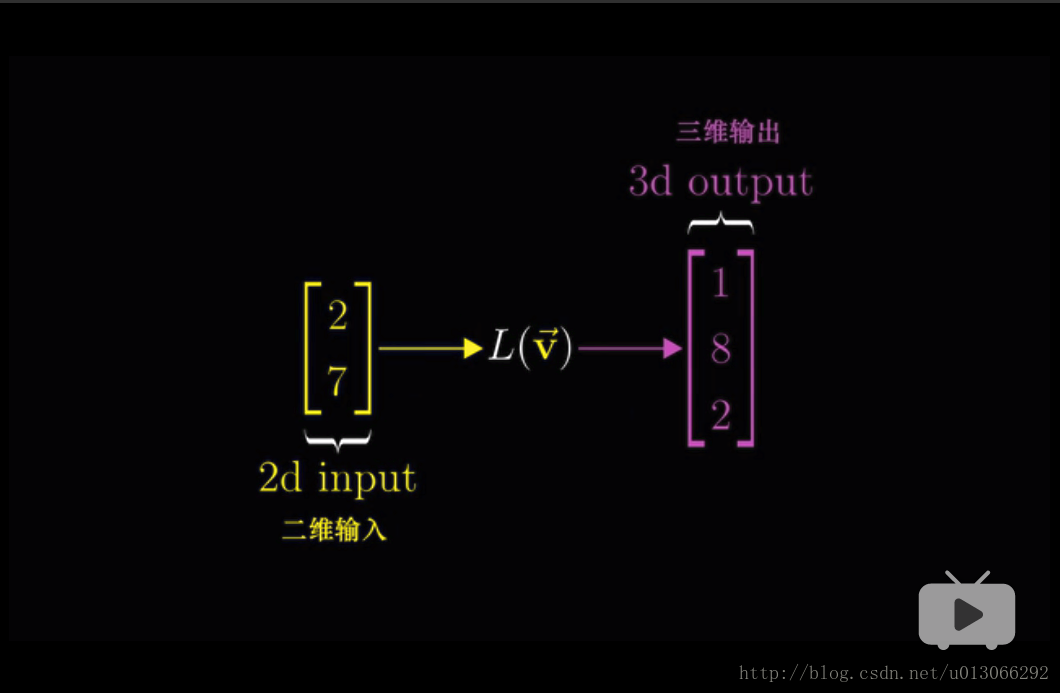
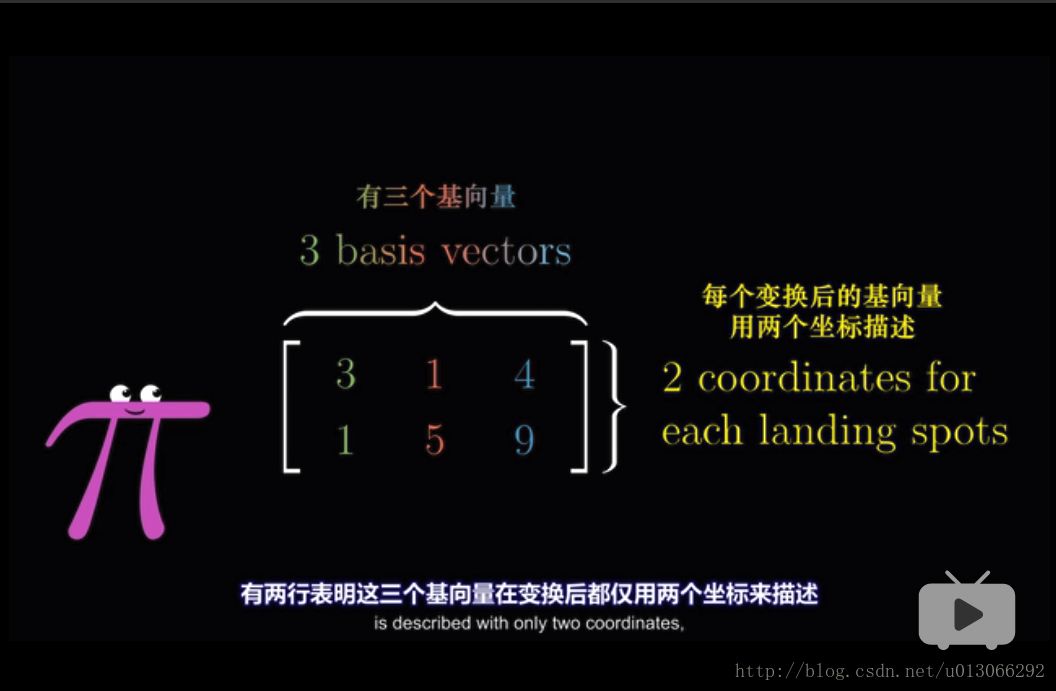
说明下,矩阵里的列数代表着这个原始矩阵的维度是多少,每一列里的行代表着这个矩阵的各个基向量的坐标表示。
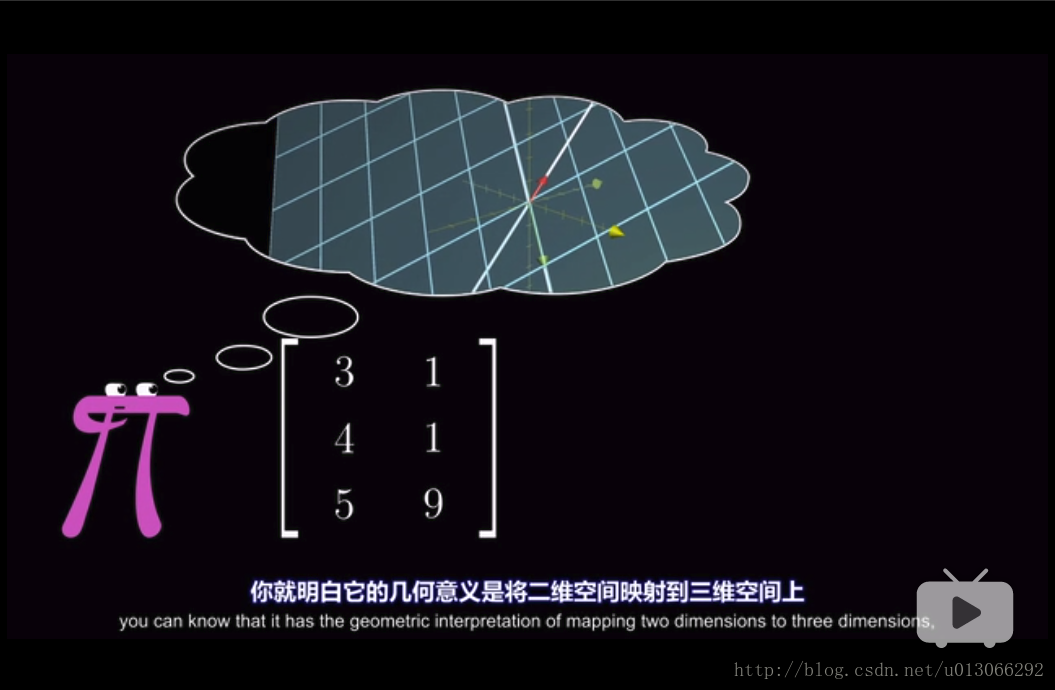
这个意味着是把一个二维的空间映射到三维的空间里(即这个二维的空间如果在三维空间里是怎样的表示的意思)。
这篇关于线性代数的本质(笔记二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!