NYOJ 237 游戏高手的烦恼 POJ3041-Asteroids ( 二分图的最大匹配 )

本文主要是介绍NYOJ 237 游戏高手的烦恼 POJ3041-Asteroids ( 二分图的最大匹配 )，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

链接：

NYOJ 237 游戏高手的烦恼：click here~~

POJ 3041 Asteroids ：click here~~

题意：

两题一样，翻译不同而已。

有一位传说级游戏高手，在闲暇时间里玩起了一个小游戏，游戏中，一个n*n的方块形区域里有许多敌人，玩家可以使用炸弹炸掉某一行或者某一列的所有敌人。他是种玩什么游戏都想玩得很优秀的人，所以，他决定，使用尽可能少的炸弹炸掉所有的敌人。

现在给你一个游戏的状态，请你帮助他判断最少需要多少个炸弹才能炸掉所有的敌人吧。

比如说，下图中X表示敌人

X . X . X .

. X .

则，他只需要炸掉第1行与第2列就能炸掉所有的敌人，所以只需要两颗炸弹就可以了。

输入

第一行是一个整数T,表示测试数据的组数(0<T<=400)。
每组测试数据的第一行有两个整数n,K，其中n表示游戏方形区域的大小。(n<=500,K<=10 000)
随后的K行，每行有两个整数i,j表示第i行，第j列有一个敌人(行和列都从1开始编号）。(1<=i,j<=n)

输出

对于每组测试数据，输出一个整数表示最少需要的炸弹颗数

样例输入

样例输出

思路：

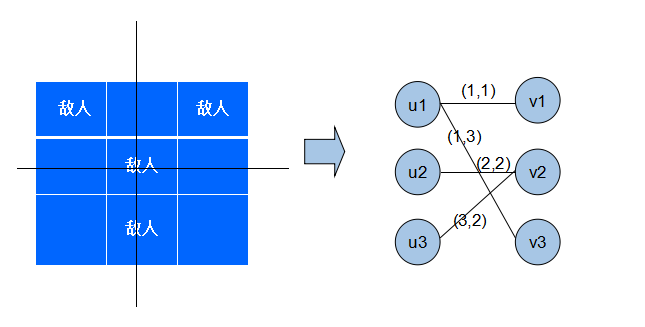
把炸弹攻击路径当作图的顶点，而把敌人当作连接路径对应的边，转化之后，攻击路径方案即对应一个顶点集合S，而要求炸弹能炸掉所有的敌人，换言之，就是构图后每一条边都至少有一个属于S的端点，如此，问题转化成求最小满足上述要求的顶点集合S。，而每个敌人所在位置对应的边，都分别与一个水平方向和一个竖直方向的顶点相连，把每一列当成一个点，每一行当成一个点，若行节点和列节点之间有边，则表明该行列该列有一个敌人。因此是二分图，运用二分图的匹配，此题还设计二分图最小点集覆盖=二分图最小匹配，相关算法知识不懂可以自学资料。

图例：

更详细的最小点覆盖数 = 最大匹配数思路：参考：click here

代码：

 
#include <math.h>
#include <queue>
#include <deque>
#include <vector>
#include <stack>
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>using namespace std;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a
#define mem(a,b) memset(a,b,sizeof(a))
int dir[4][2]= {{1,0},{-1,0},{0,1},{0,-1}};
const int maxn=502;
struct Edge
{int v;
};
int n, k;
vector <int >  mapp[maxn];
int vis[maxn], connect[maxn];
int dfs(int u)
{int i;for(i =0; i<mapp[u].size(); i++){int xx=mapp[u][i];if(!vis[xx]){vis[xx] =1;if (!connect[xx]|| dfs(connect[xx])){connect[xx] = u;return 1;}}}return 0;
}
int main()
{//freopen("1.txt","r",stdin);//freopen("2.txt","w",stdout);int cas;scanf("%d",&cas);while(cas--){int sum=0;scanf("%d%d", &n, &k);for (int i =0; i <maxn; i++) mapp[i].clear();for (int i =1; i <=k; i++){int a, b;scanf("%d%d", &a, &b);mapp[a].push_back(b);}memset(connect,0, sizeof(connect));for(int i =1; i <=n; i++){memset(vis, 0, sizeof(vis));if (dfs(i))sum++;}printf("%d\n",sum);}return 0;
}

优化代码（）：

 
#include <stdio.h>
#include <string.h>const int N = 505;
const int M = 10005;struct Vertex
{int head;
}V[N];struct Edge
{int v,next;
}E[M];int top,match[N];bool used[N];void Init()
{top = 0;memset(V,-1,sizeof(V));memset(match,0,sizeof(match));
}void Add_Edge(int u,int v)
{E[top].v = v;E[top].next = V[u].head;V[u].head = top++;
}bool dfs(int u)
{for(int i=V[u].head;~i;i=E[i].next){int v = E[i].v;if(!used[v]){used[v] = true;if(!match[v] || dfs(match[v])){match[v] = u;return true;}}}return false;
}int maxMatch(int n)
{int ans = 0;for(int i=1;i<=n;i++){memset(used,false,sizeof(used));if(dfs(i))++ans;}return ans;
}int main()
{int z,n,m,num;scanf("%d",&z);while(z--){Init();scanf("%d%d",&n,&m);while(m--){int i,j;scanf("%d%d",&i,&j);Add_Edge(i,j);}printf("%d\n",maxMatch(n));}return 0;
}