Uva | Cutting Sticks

本文主要是介绍Uva | Cutting Sticks，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原题

You have to cut a wood stick into pieces. The most affordable company, The Analog Cutting Machinery,Inc. (ACM), charges money according to the length of the stick being cut. Their procedure of work requires that they only make one cut at a time.
It is easy to notice that different selections in the order of cutting can led to different prices. For example, consider a stick of length 10 meters that has to be cut at 2, 4 and 7 meters from one end.
There are several choices. One can be cutting first at 2, then at 4, then at 7. This leads to a price of 10 + 8 + 6 = 24 because the first stick was of 10 meters, the resulting of 8 and the last one of 6.
Another choice could be cutting at 4, then at 2, then at 7. This would lead to a price of 10 + 4 + 6 = 20, which is a better price.
Your boss trusts your computer abilities to find out the minimum cost for cutting a given stick.

Sample Input
100
3
25 50 75
10
4
4 5 7 8
0
Sample Output
The minimum cutting is 200.
The minimum cutting is 22.

最近在看DP，看到了区间DP的相关内容，于是便自己动手推了推一些东西，这样对这个了解可以深刻一点。

思考过程

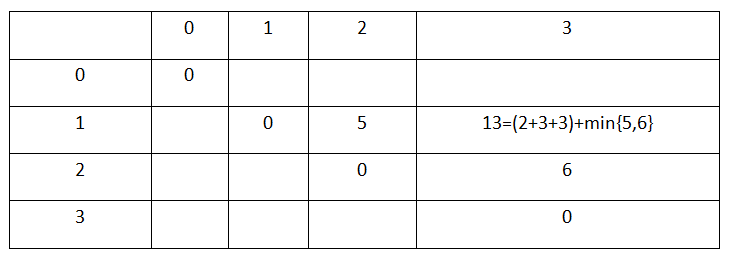
首先给出的几个切点跟它整体的长度并没有什么关系，而且对于一个切点来说，它所产生的影响是这一段的总长度而不是切点的位置。
所以在尝试列了这么一个表格之后无果：
用例是10，切点2、4、7
使用dp[i][j]表示状态转移
表格1
是的，以切点为阶段列出矩阵，发现根本无法正确求解。
切点0【位置为2】和0产生了10，1和1产生了10，然后想再往下推导发现无从下手。

错误之处在于这根本就不是一个可以进行递推的状态，下一状态和当前状态的关系并没有显现出来，也就无法进行DP了。

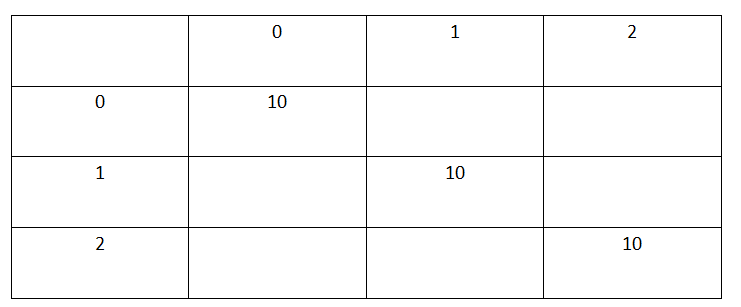
然后突然想到是不是可以对切之后的小块长度进行分析；
表格2
对于长度为10，切点为2、4、7的情况可以转化为上述图形所表示的情境。
不过当时还是没有脱离切的次数作为阶段，这个思想；
于是列出了错误的下表：
表格3
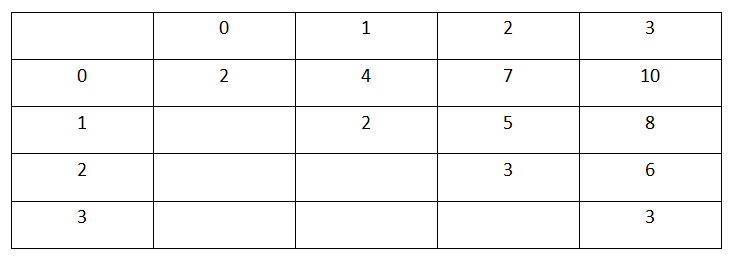
如上图，[0][0]表示取第一段，[0][1]表示取第1，2段…然后….
还是不对，这样一来肯定是10啊。

问题出在切木棍的时候，是会重复计算某一段的。
而像我所列的这个式子，在[0][2]的时候，并没有去判断子问题，也没有算当前切割会产生什么效果(╯‵□′)╯︵┻━┻

所以就在思考划分子问题（/(ㄒoㄒ)/~~ 这才是正确DP思路啊喂之前在想什么呢）

正确的思维开始

我们逆向思维，考虑将一根根短木棍拼接成一个长木棍的情况。
表格4
表格2
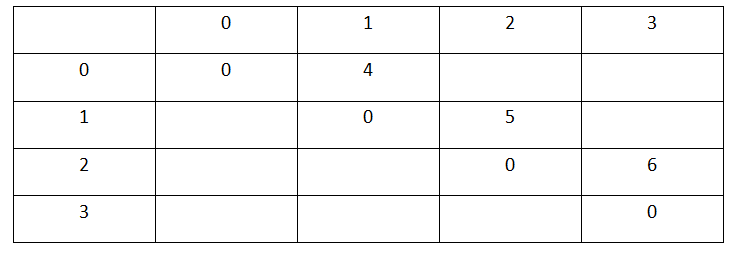
那么如上图，取第0块和第1块，第1块和第2块，第2块和第3块的代价很容易计算出来是4，5，6；

然后想到Tushar Roy的课程中，包括计算最小矩阵连乘次数的时候，他所使用的方式似乎都是一个个小区间做。
在此安利一下这个视频，需翻墙：https://www.youtube.com/watch?v=vgLJZMUfnsU&list=PLrmLmBdmIlpsHaNTPP_jHHDx_os9ItYXr&index=3

回顾一下在矩阵链乘时候他的做法【虽然我和他的推导方式不太一样但是实质都是区间DP】：
表格4
对于这道题，我们也可以用类似的方法：
表格5
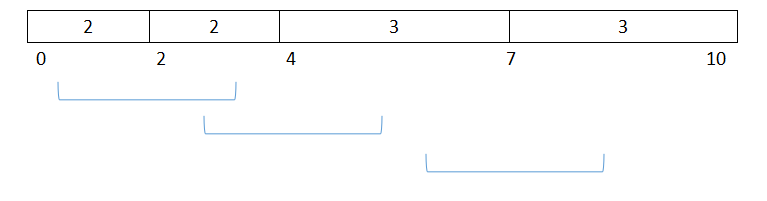
当len=2的时候，可以得到相应的长度为4，5，6；
同理，len=3的时候
表格6
看到这一步，状态的转移就非常明显了，而我们也可以就此继续推导到剩余所有的值。而dp[0][3]即是我们要求的整个木棍的分割产生的价值量。

整理一下思路重新出发：
对于长度为10，切点为2、4、7的木棍
可以将其切分为2、2、3、3一共4段
其DP方程为：
dp[i][j]=0 if i==j 显然单段木棍是不不需要切分不会产生cost
sum[i~j]+min{dp[i][k]+dp[k+1][j]} if i<=k < j
即当需要切分的时候，所需要的cost为整段木棍的长度【sum】和其子问题切分所需要的cost。

完美收官。

代码

对于DP的方式，我一开始是采取同我所写的矩阵链乘同样的求法，采用逆推的方式
表格7

因为dp方程里面，dp[i][j]所依赖的状态dp[i][k]、dp[k+1][j]必须出现在[i][j]之前，所以要想得出它们必须得倒推才能得出正确的结果；
代码如下：

for(int i=n;i>=0;i--){for(int j=i+1;j<n;j++){int min=INT_MAX;//需要计算i~j的总量int sum=0;for(int k=i;k<=j;k++) sum+=woods[k];for(int k=i;k<j;k++){if(dp[i][k]+dp[k+1][j]<min)min=dp[i][k]+dp[k+1][j];}dp[i][j]=sum+min;}
}

在参考了网上的一篇博客之后：
参考链接：http://www.cnblogs.com/zsboy/archive/2013/03/08/2950261.html

感觉写成这样才更加符合区间DP的性质

//遍历长度 
for(int len=1;len<=n;len++){//长度不可以超过总长 for(int i=0;i<n && i+len<n;i++){int j=i+len;//结束点//需要计算i~j的总量int sum=0;int min=INT_MAX;for(int k=i;k<=j;k++) sum+=woods[k];//状态转移for(int k=i;k<j;k++){if(dp[i][k]+dp[k+1][j]<min)min=dp[i][k]+dp[k+1][j];}dp[i][j]=sum+min;}
}

感觉这和很久以前看的石子合并问题如出一辙【当时太渣完全看不懂在说什么】，只是石子合并的问题没有那个sum选项而已。
于是我们引入

区间DP

区间动态规划问题一般都是考虑，对于每段区间，他们的最优值都是由几段更小区间的最优值得到，是分治思想的一种应用，
将一个区间问题不断划分为更小的区间直至一个元素组成的区间，枚举他们的组合，求合并后的最优值。
设F[i,j]（1<=i<=j<=n）表示区间[i,j]内的数字相加的最小代价
最小区间F[i,i]=0（一个数字无法合并，∴代价为0）

每次用变量k（i<=k<=j-1）将区间分为[i,k]和[k+1,j]两段

For p:=1 to n do // p是区间长度，作为阶段。
for i:=1 to n do // i是穷举的区间的起点
begin
j:=i+p-1; // j是区间的终点，这样所有的区间就穷举完毕
if j>n then break; // 这个if很关键。
for k:= i to j-1 do // 状态转移，去推出 f[i,j]
f[i , j]= max{f[ i,k]+ f[k+1,j]+ w[i,j] }
end;
这个结构必须记好，这是区间动态规划的代码结构

小结

一道题的解题报告写了2个小时，在不明白什么是区间DP的情况下【虽然看过无数的概念但是之前还是完全懵逼】，一点点分析和解决问题。
这些碰壁的经验对于读者可能没有什么价值，但是对于自己的价值还是蛮大的。
初学DP，也谈不上什么经验，但是觉得如果自己独立推导出来，可以对这些阶段、状态、决策有着更加深入的认识。

这篇关于Uva | Cutting Sticks的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！