机器学习与数据挖掘（2）：学习的可能性

本文主要是介绍机器学习与数据挖掘（2）：学习的可能性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

误差理论

① 偏倚（bias）和方差(variance)

在讨论线性回归时，我们用一次线性函数对训练样本进行拟合（如图1所示）；然而，我们可以通过二次多项式函数对训练样本进行拟合（如图2所示），函数对样本的拟合程序看上去更“好”；当我们利用五次多项式函数对样本进行拟合（如图3所示），函数通过了所有样本，成为了一次“完美”的拟合。

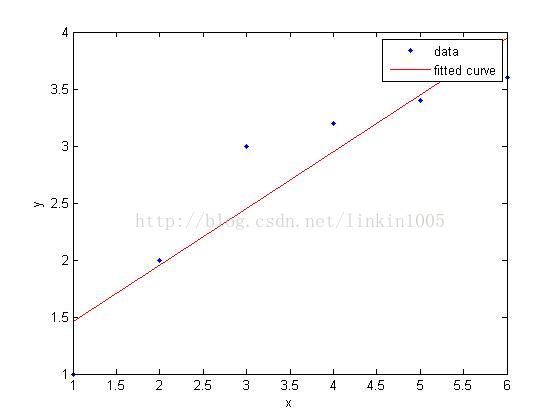
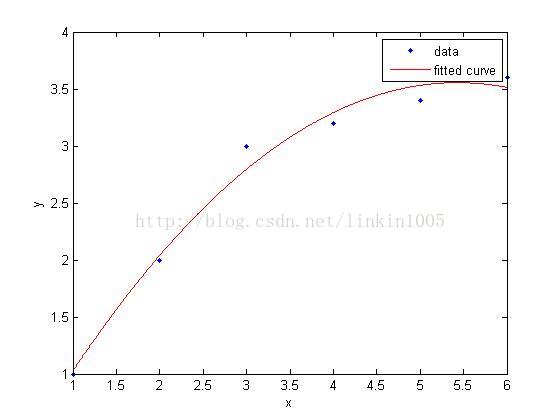
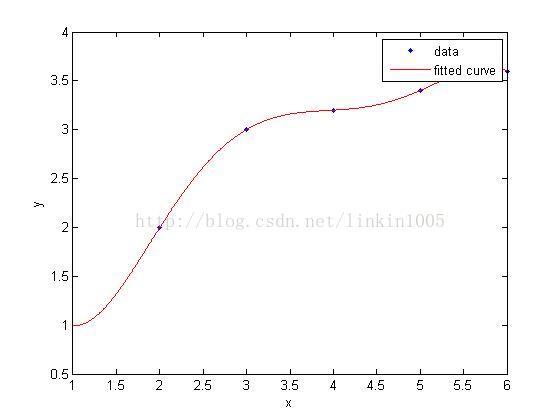
图3建立的模型，在训练集中通过x可以很好的预测y，然而，我们却不能期望该模型能够很好的预测训练集外的数据。换句话说，这个模型没有很好的泛化能力。因此，模型的泛化误差(generalization error)不仅包括其在样本上的期望误差，还包括在训练集上的误差。

图1和图3中的模型都有较大的泛化误差，然而他们的误差原因却不相同。图1建立了一个线性模型，但是该模型并没有精确的捕捉到训练集数据的结构，我们称图1有较大的偏倚（bias），也称欠拟合；图3通过5次多项式函数很好的对样本进行了拟合，然而，如果将建立的模型进行泛化，并不能很好的对训练集之外数据进行预测，我们称图3有较大的方差（variance），也称过拟合。

通常，在偏倚和方差之间，这样一种规律：如果模型过于简单，其具有大的偏倚，而如果模型过于复杂，它就有大的方差。调整模型的复杂度，建立适当的误差模型，就变得极其重要了。

② 预备知识

首先我们先介绍两个非常有用的引理：

引理1

一致限（the union bound）令 $A_1,A_2,A_3,A_4,\dots,A_k$ 为k个不同的事件（不一定相互独立），那么有：

P (A 1 \cup A 2 \dots \cup A k) \leq P (A 1) + \dots + P (A k)

$P(A_1\cup A_2 \dots \cup A_k)\leq P(A_1) + \dots + P(A_k)$

一致限说明：k个事件中任一个事件发生的概率小于等于这k个事件发生的概率和（等号成立的条件为这k个事件相两两互斥）。

引理2

Hoeffding不等式（Hoeffding’s inequality）令 $Z_1,Z_2,Z_3,Z_4,\dots,Z_m$ 为m个独立同分布的随机变量，由参数为 $\phi$ 的伯努利分布（特殊的二项分布，即 $P(Z_i=1)=\phi,\ P(Z_i=0)=1-\phi$ ）生成。令， $\hat{\phi}=\frac{1}{m}\sum_{i=1}^m{Z_i}$ 为这些随机变量的均值，对于任意 $\gamma > 0$ 有：

P (| ϕ - ϕ^| > γ) \leq 2 e - 2 γ 2 m

$P(|\phi - \hat{\phi}|>\gamma)\leq 2e^{-2\gamma^2m}$

P (| ϕ - ϕ^| \leq γ) > 1 - 2 e - 2 γ 2 m

$P(|\phi - \hat{\phi}|\leq\gamma)> 1 - 2e^{-2\gamma^2m}$

Hoeffding刻画的是某个事件的真实概率及其m个独立重复试验中观察到的频率之间的差异，更准确的将，它是应用于m个不同的伯努利实验。

在机器学习中，引理2称为Chernoff边界（Chernoff bound）,它说明：假设我们用随机变量的均值 $\hat{\phi}$ 去估计参数 $\phi$ ，估计的参数和实际参数的差超过一个特定数值的概率有一确定的上界，并且随着样本量m的增大， $\hat{\phi}$ 与 $\phi$ 很接近的概率也越来越大。

通过以上两个引理，我们能够引出机器学习中很重要结论。

为简单起见，我们只讨论二分类问题，即类标签为 $y\in \{0, 1\}$ 。

假设给定的训练集为 $S=\{(x^{(i)}, y^{(i)}); i=1,\dots,m\}$ ，且各训练样本 $(x^{(i)}, y^{(i)})$ 独立同分布，皆为某个特定分布D生成。对于一个假设函数（hypothesis），定义训练误差（training error）（也称为经验风险（empirical risk）或经验误差(empiriacal error)）为：