吴恩达机器学习第三课 week2 推荐算法（上）

本文主要是介绍吴恩达机器学习第三课 week2 推荐算法（上），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

01 学习目标

02 推荐算法

2.1 定义

2.2 应用

2.3 算法

03 协同过滤推荐算法

04 电影推荐系统

4.1 问题描述

4.2 算法实现

05 总结

01 学习目标

（1）了解推荐算法

（2）掌握协同过滤推荐算法（Collaborative Filtering Recommender Algorithm）原理

（3）利用协同过滤算法实现“电影推荐系统”

02 推荐算法

2.1 定义

推荐算法是信息过滤系统中的一种技术，旨在预测用户对未接触过的物品的喜好程度，并据此向用户推荐相应的物品。

2.2 应用

推荐系统广泛应用于电商、社交媒体、音视频平台、新闻资讯等领域，可以提升用户体验、增加用户黏性和促进内容发现。

2.3 算法

推荐算法大致可以分为以下几类：

03 协同过滤推荐算法

下面基于一个生活场景来理解协同过滤算法的推荐逻辑。

假设小强在上午11:30打开饱了么外卖APP搜索附近的菜馆，小强只在APP上进行一次评分，且APP有家最近上架的新菜馆“老狼大盘鸡”。小强进入APP最先看到的会是哪家菜馆呢？我们来算一下！

假设下表中为该APP的全部数据（表中？表示未评过分或系统无法归类的菜馆）：

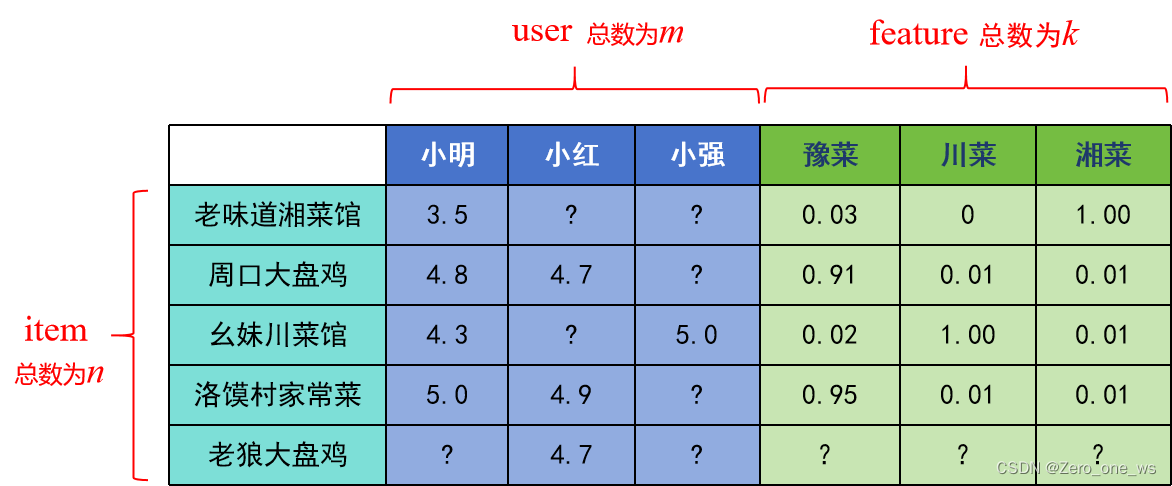
基于表中数据，可以提取以下数组（“0”替换“?”）：

菜品特征矩阵（值：0~1）：

$\textbf{X}_{n\times k}=\begin{bmatrix} 0.03 &0 &1 \\ 0.91& 0.01 & 0.01\\ 0.02& 1 &0.01 \\ 0.95 & 0.01 &0.01 \\ 0&0 & 0 \end{bmatrix}$

用户评分矩阵：

$\textbf{Y}_{n\times m}=\begin{bmatrix} 3.5 &0 &0 \\ 4.8& 4.7 & 0\\ 4.3& 0 &5.0 \\ 5.0 & 4.9 &0 \\ 0&4.7 & 0 \end{bmatrix}$

评分判断矩阵（已评为1、未评为0）：

$\textbf{R}_{n\times m}=\begin{bmatrix} 1 &0 &0 \\ 1& 1 & 0\\ 1& 0 &1 \\ 1 & 1 &0 \\ 0&1 & 0 \end{bmatrix}$

此外，再构造一个用户参数矩阵W和用户参数向量b：

$\textbf{W}_{m\times k}=\begin{bmatrix} w_{11} &w_{12} &w_{13} \\ w_{21}& w_{22} & w_{23}\\ w_{31}& w_{32} &w_{33} \\ w_{41} & w_{42} &w_{43} \\ w_{51}&w_{52} & w_{53} \end{bmatrix}$

$\textbf{b}_{1\times m}=\begin{bmatrix} b_{11} &b_{12}&b_{13} \end{bmatrix}$

由以上5个矩阵，可以构造出预测用户评分的一般式如下：

$\textbf{Y}=\textbf{R}*(\textbf{X}\cdot \textbf{W}^T+\textbf{b})=\frac{1}{2}\sum_{j=0}^{n-1}\sum_{i=0}^{m-1}R^{(i,j)}*(W^{(j)}\cdot X^{(i)}+b^{(j)}-Y^{(i,j)})^2$

式中，参数阵W和b采用梯度下降法计算得到，同时为防止参数过拟合，成本函数增加正则项，如下所示：

$J(\textbf{W},\textbf{b},\textbf{X})=\textbf{Y}+\frac{\lambda }{2}\sum_{i=0}^{m-1}\sum_{t=0}^{k}(X_t^{(i)})^2+\frac{\lambda }{2}\sum_{j=0}^{n-1}\sum_{t=0}^{k}(W_t^{(j)})^2$

由于部分菜馆（老狼大盘鸡）的特征未知，因此增加了X的正则项。饱了么APP会根据成本最小原则预测出参数W和b及特征X，进而得到每位用户对不同菜馆的预测分数。最后预测出的小强的评分高低排序后，依次进行推荐，如下：

计算结果表明，口碑最好且“小强”没评过分（可能没吃过）的“洛馍村家常菜”排在最前面；而“老狼大盘鸡”是新上的菜馆，其排名竟然是第二，这可能是饱了么的常客“小红”的评论发挥了作用；第三名是“小强”曾经给过高分的“幺妹川菜馆”。完整代码如下：

# 导包
import numpy as np
import tensorflow as tf
from tensorflow import keras# 数据准备
X = np.array([[0.03, 0, 1], [0.91, 0.01, 0.01], [0.02, 1, 0.01], [0.95, 0.01, 0.01], [0, 0, 0]])
Y = np.array([[3.5, 0, 0], [4.8, 4.7, 0], [4.3, 0, 5], [5, 4.9, 0], [0, 4.7, 0]])
R = np.array([[1, 0, 0], [1, 1, 0], [1, 0, 1], [1, 1, 0], [0, 1, 0]])
label_ = ['老味道湘菜馆','周口大盘鸡','幺妹川菜馆','洛馍村家常菜','老狼大盘鸡']# 定义归一化函数、成本函数
def normalizeRatings(Y, R):Ymean = (np.sum(Y*R,axis=1)/(np.sum(R, axis=1)+1e-12)).reshape(-1,1)Ynorm = Y - np.multiply(Ymean, R) return(Ynorm, Ymean)def cofi_cost_func(X, W, b, Y, R, lambda_):"""Returns the cost for the content-based filteringArgs:X (ndarray (num_movies,num_features)): matrix of item featuresW (ndarray (num_users,num_features)) : matrix of user parametersb (ndarray (1, num_users)            : vector of user parametersY (ndarray (num_movies,num_users)    : matrix of user ratings of moviesR (ndarray (num_movies,num_users)    : matrix, where R(i, j) = 1 if the i-th movies was rated by the j-th userlambda_ (float): regularization parameterReturns:J (float) : Cost"""error = tf.linalg.matmul(X, tf.transpose(W)) + b - Yj = tf.boolean_mask(error, tf.cast(R, tf.bool)) ** 2J = 0.5 * tf.reduce_sum(j) + (lambda_ / 2) * (tf.reduce_sum(X **2) + tf.reduce_sum(W **2))return J# 归一化处理
Ynorm, Ymean = normalizeRatings(Y, R)# 定义模型
n, m = Y.shape
k =3tf.random.set_seed(1234)
W = tf.Variable(tf.random.normal((m, k), dtype=tf.float64), name='W')
X = tf.Variable(tf.random.normal((n, k), dtype=tf.float64), name='X')
b = tf.Variable(tf.random.normal((1, m), dtype=tf.float64), name='b')optimizer = keras.optimizers.Adam(learning_rate=0.005)# 训练模型
iterations = 200
lambda_ = 1
for iter in range(iterations):with tf.GradientTape() as tape:cost = cofi_cost_func(X, W, b, Ynorm, R, lambda_)grads = tape.gradient(cost, [X, W, b])optimizer.apply_gradients(zip(grads, [X, W, b]))if iter %20 == 0:print(f'第{iter}次迭代的成本为：{cost.numpy()}')# 预测分数
y = np.matmul(X, np.transpose(W)) + b
y_m = y + Ymean    # 恢复数值
pred = y_m[:,1]    # 选择小强的结果
ix = tf.argsort(pred, direction='DESCENDING')  # 降序排列# 推荐
for i in range(len(ix)):print(f'top{i +1}:{label_[ix[i]]},预测评分:{pred[ix[i]]:0.2f}')

协同过滤（Collaborative Filtering, CF）中的“协同”二字，其核心意义在于“合作”或“协同工作”，“协同”本质是通过分析用户群或物品群之间的共同行为模式，来推断和预测单个用户的潜在喜好，从而实现个性化推荐。在推荐系统领域，这种“协同”体现在算法利用大量用户的行为数据（如评分、购买历史、浏览记录等），通过分析用户之间的共同偏好或者物品之间的相似性，来实现对用户可能感兴趣但尚未直接接触的物品的推荐。

具体来说，协同过滤算法分为两大类：

用户协同过滤（User-based Collaborative Filtering）：在这种方法中，“协同”意味着算法寻找与目标用户兴趣相似的其他用户群体。算法分析这些相似用户喜欢的物品，并基于这些相似用户的偏好来推荐物品给目标用户。这里，用户之间的“协同”体现在他们的共同兴趣和行为模式上。
物品协同过滤（Item-based Collaborative Filtering）：在物品协同过滤中，“协同”的概念体现为算法识别出经常被相同用户喜欢的物品集合，即使这些用户之间可能没有直接的相似性。换句话说，如果用户A喜欢物品X和Y，用户B也喜欢物品X，那么就可以推断用户B可能也会喜欢物品Y。这里，物品之间的“协同”是基于它们被共同评价或消费的模式。

04 电影推荐系统

4.1 问题描述

GroupLens 是明尼苏达大学双城分校计算机科学与工程系的一个研究实验室，专注于推荐系统、在线社区、移动和无处不在技术、数字图书馆和本地地理信息系统等领域。

我们从GroupLens网站的 MovieLens 栏目下载电影数据集，用于构建“电影推荐系统”。

4.2 算法实现

（1）导入所需模块

import numpy as np
import tensorflow as tf
from tensorflow import keras
from recsys_utils import *

（recsys_utils模块内有数据读取函数load_precalc_params_small、load_ratings_small、load_Movie_List_pd以及归一化函数normalizeRatings）

（2）数据读取

# 读取数据
X, W, b, num_movies, num_features, num_users = load_precalc_params_small()
Y, R = load_ratings_small()
# 读取电影信息并提取名称列
movieList, movieList_df = load_Movie_List_pd()print("Y", Y.shape, "R", R.shape)
print("X", X.shape)
print("W", W.shape)
print("b", b.shape)
print("num_features", num_features)
print("num_movies",   num_movies)
print("num_users",    num_users)
print("movieList:\n",movieList[:5])
print("movieList_df:\n",movieList_df[:5])

运行以上代码，结果如下：

（原始数据集包含由600名用户对9000部电影进行的评价。为了专注于2000年以后的电影，我们将数据集的规模缩小至包含443名用户和4778部电影。该数据集在0.5到5的范围内对电影进行评分，以0.5的步长递增）

（3）定义成本函数

def cofi_cost_func_v(X, W, b, Y, R, lambda_):"""Returns the cost for the content-based filteringVectorized for speed. Uses tensorflow operations to be compatible with custom training loop.Args:X (ndarray (num_movies,num_features)): matrix of item featuresW (ndarray (num_users,num_features)) : matrix of user parametersb (ndarray (1, num_users)            : vector of user parametersY (ndarray (num_movies,num_users)    : matrix of user ratings of moviesR (ndarray (num_movies,num_users)    : matrix, where R(i, j) = 1 if the i-th movies was rated by the j-th userlambda_ (float): regularization parameterReturns:J (float) : Cost"""j = (tf.linalg.matmul(X, tf.transpose(W)) + b - Y)*RJ = 0.5 * tf.reduce_sum(j**2) + (lambda_/2) * (tf.reduce_sum(X**2) + tf.reduce_sum(W**2))return J

（tf.linalg.matmul(X, tf.transpose(W)) 是一个使用 TensorFlow 库的矩阵乘法函数，其中 X 和 W 是两个张量（tensor），tf.transpose(W) 表示对张量 W 进行转置）

（4）目标用户数据提取

假设推荐目标用户是Tony，Tony的历史评分如下（我们手动添加）：

my_ratings = np.zeros(num_movies)          #  Initialize my ratings# 手动添加Tony的评分
my_ratings[2700] = 5   # Toy Story 3 (2010)
my_ratings[2609] = 2   # Persuasion (2007)
my_ratings[929]  = 5   # Lord of the Rings: The Return of the King, The
my_ratings[246]  = 5   # Shrek (2001)
my_ratings[2716] = 3   # Inception
my_ratings[1150] = 5   # Incredibles, The (2004)
my_ratings[382]  = 2   # Amelie (Fabuleux destin d'Amélie Poulain, Le)
my_ratings[366]  = 5   # Harry Potter and the Sorcerer's Stone (a.k.a. Harry Potter and the Philosopher's Stone) (2001)
my_ratings[622]  = 5   # Harry Potter and the Chamber of Secrets (2002)
my_ratings[988]  = 3   # Eternal Sunshine of the Spotless Mind (2004)
my_ratings[2925] = 1   # Louis Theroux: Law & Disorder (2008)
my_ratings[2937] = 1   # Nothing to Declare (Rien à déclarer)
my_ratings[793]  = 5   # Pirates of the Caribbean: The Curse of the Black Pearl (2003)
# 已评分电影的索引
my_rated = [i for i in range(len(my_ratings)) if my_ratings[i] > 0]# 将Tony的评分及相应的布尔数组添加至原数据中
Y = np.c_[my_ratings, Y]
R = np.c_[(my_ratings != 0).astype(int), R]print("\n(New user)Tony's ratings:\n")
for i in range(len(my_ratings)):if my_ratings[i] > 0 :print(f'Rated {my_ratings[i]} for  {movieList_df.loc[i,"title"]}')

（"my_rated = [i for i in range(len(my_ratings)) if my_ratings[i] > 0]": range(len(my_ratings)) 会生成一个从0到 len(my_ratings)-1 的整数序列，如果 my_ratings[i]大于0，那么i 就会被添加到 my_rated 列表中）

（my_ratings != 0将my_ratings 中不等于0的数转为true，等于0的数转为false（布尔数组），astype(int) 将该布尔数组转换为整数数组（0和1）然后用np.c_[] 将两个布尔数组按列合并）

运行以上代码，结果如下：

（5）数据归一化

Ynorm, Ymean = normalizeRatings(Y, R)

（6）定义模型

num_movies, num_users = Y.shape
num_features = 100# 采用tf.Variable 初始化参数
tf.random.set_seed(1234) # for consistent results
W = tf.Variable(tf.random.normal((num_users,  num_features),dtype=tf.float64),  name='W')
X = tf.Variable(tf.random.normal((num_movies, num_features),dtype=tf.float64),  name='X')
b = tf.Variable(tf.random.normal((1,          num_users),   dtype=tf.float64),  name='b')# 设置优化器、学习率
optimizer = keras.optimizers.Adam(learning_rate=1e-1)

（7）训练模型

iterations = 200
lambda_ = 1
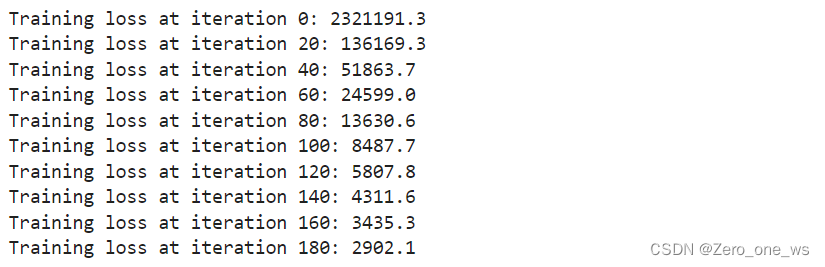
for iter in range(iterations): # 使用TensorFlow的GradientTape记录用于计算成本的操作with tf.GradientTape() as tape:# Compute the costcost_value = cofi_cost_func_v(X, W, b, Ynorm, R, lambda_)# 使用梯度记录器自动获取可训练变量相对于损失的梯度。grads = tape.gradient( cost_value, [X,W,b] )# 通过更新变量的值来进行一次梯度下降，以使损失函数达到最小值。optimizer.apply_gradients( zip(grads, [X,W,b]) )# 打印进度if iter % 20 == 0:print(f"Training loss at iteration {iter}: {cost_value:0.1f}")

运行以上代码，结果如下：

（8）电影推荐

# 计算概率
p = np.matmul(X.numpy(), np.transpose(W.numpy())) + b.numpy()
# 归一化恢复
pm = p + Ymean
# 提取Tony的数据
my_predictions = pm[:,0]
# sort predictions返回降序索引
ix = tf.argsort(my_predictions, direction='DESCENDING')# 推荐Tony未评价过的电影（从预测评分top17的电影中挑选）
for i in range(17):j = ix[i]if j not in my_rated:print(f'Predicting rating {my_predictions[j]:0.2f} for movie {movieList[j]}')# 测试比对user评分的真实值与预测值
print('\n\nOriginal vs Predicted ratings:\n')
for i in range(len(my_ratings)):if my_ratings[i] > 0:print(f'Original {my_ratings[i]}, Predicted {my_predictions[i]:0.2f} for {movieList[i]}')

运行以上代码，结果如下：