本文主要是介绍最长考拉兹序列,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- 题目:
考虑如下定义在正整数集上的迭代规则:
n n/2 (若n为偶数)
n 3n+1 (若n为奇数)
从13开始,可以迭代生成如下的序列:
13 40
20
10
5
16
8
4
2
1
可以看出这个序列(从13开始到1结束)共有10项。 尽管还未被证明,但普遍认为,从任何数开始最终都能抵达1并结束, 这被称为 “考拉兹序列”。
在小于100万的数中,从哪个数开始迭代生成的序列最长?
注:在迭代过程中允许出现超过一百万的项(例如,题目中的序列,第二项40就比第一项13大)。
- 题目分析:
根据题目描述,我们可以知道这是一道枚举类型的题,
- 代码实现
//代码段1
#include <stdio.h>#define MAX_N 1000000int cal_len(int n){if(n == 1) return 1;if(n & 1) return cal_len(3*n +1)+1;return cal_len(n>>1)+1;
}int main(){int ans = 0, len = 0;for(int i = 1;i <= MAX_N;i++){int temp_len = cal_len(i);if(temp_len <= len) continue;len = temp_len;ans = i;}printf("ans = %d, len = %d\n",ans, len);return 0;
}小技巧:
在函数 int cal_len(long long n) 中,判断当前n值是否为偶数,没有使用模运算 if(n % 2 ) 而是使用了 位运算 if(n & 1 ) , 这是因为位运算的运算效率更快 ,(n& 1) 为真值,说明n是奇数。 同样在,n/2 运算也写成了位运算 n >> 1.
- 运行结果
![]()
- 运行结果分析
程序报错崩溃了,这个报错结果表示“访问了非法内存”,造成这个报错的原因可以有以下几种情况:
1)访问未被分配或已释放的内存区域;
2)使用空指针或野指针进行读写操作;
3)数组越界访问,例如通过错误的下标访问数组元素;
4)非法指针操作,如未经授权的指针转换或解引用非合法的内存地址;
5)堆栈溢出,通常由于局部变量过大或递归调用过深导致;
6)多线程编程中使用了线程不安全的函数或未加锁保护共享资源;
7)对常量或只读内存区域的非法写入操作。
如何避免出现这个报错?
1)正确的使用指针;
确保所有指针在使用前都进行了初始化,并在不再需要时及时释放;避免使用野指针,特别是不要随意假设指针指向的内存是可用的。
2)数组的访问
不要出现数组的越界访问,例如通过错误的下标访问数组元素;
3)动态内存管理
在程序员自己进行内存分配时,确保内存分配后要有对应的释放操作,避免出现内存泄漏;
4)多线程环境
如果使用了多线程编程,要合理使用互斥锁或其他同步机制来保护共享资源。
经过上述分析,我们进一步分析代码段1出现崩溃的原因可能是什么,代码中使用了递归调用,会不会是递归调用的层数太深,栈中装不下了呢?但是在cal_len 函数中,即使递归层数比较深,每一次进行函数调用所需要的空间仅是一个整型值再加上一个函数指针的大小,所以,我们猜测他不是因为空间上存不下了,那会不会是函数本身陷入了死循环?这个函数如果想结束,需要满足条件 n==1, 如果这个条件不会出现呢?那就进入死循环。n在变化的过程中,超出了int 所能表示的范围,成为了负数,就会出现这个结果。我们来验证一下, n是否出现了负数。
//代码段2
#include <stdio.h>#define MAX_N 1000000int cal_len(int n){if(n == 1) return 1;if(n < 0) printf("n < 0 ,error");if(n & 1) return cal_len(3*n +1)+1;return cal_len(n>>1)+1;
}int main(){int ans = 0, len = 0;for(int i = 1;i <= MAX_N;i++){int temp_len = cal_len(i);if(temp_len <= len) continue;len = temp_len;ans = i;}printf("ans = %d, len = %d\n",ans, len);return 0;
}运行结果:
运行结果显示,果然出现了负数,说明数据溢出了,即当前的int类型存不下实际数据的长度,应该改为long long 类型。
//代码段3
#include <stdio.h>#define MAX_N 1000000int cal_len(long long n){if(n == 1) return 1;if(n & 1) return cal_len(3*n +1)+1;return cal_len(n>>1)+1;
}int main(){int ans = 0, len = 0;for(int i = 1;i <= MAX_N;i++){int temp_len = cal_len(i);if(temp_len <= len) continue;len = temp_len;ans = i;}printf("ans = %d, len = %d\n",ans, len);return 0;
}运行结果:
![]()
- 代码优化:
代码段3运行时间:
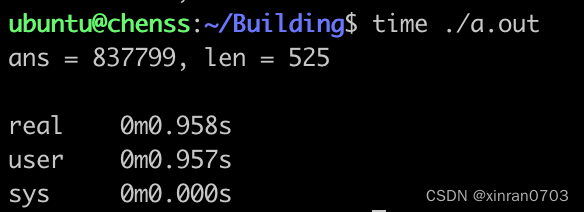
现在将数据规模由100万增加到1000万:
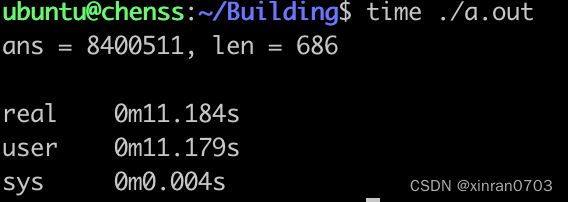
结果显示,运行时间也增加了10倍多,可见这段代码的耗时是较长的,提高运行时间就是我们优化的目标,那么,这段这段代码为什么会如此耗时?
分析递归调用的过程:
如果当前遍历到 i = 10, 那么我们得到的迭代序列是:
10 5
16
8
4
2
1, len = 7;
如果当前遍历到 i = 13, 得到的迭代序列是:
13 40
20
10
5
16
8
4
2
1, len = 10;
这两段迭代过程是有重复的,当i= 13 时,序列10 之后的迭代过程在 i = 10 时已经计算过了,所以如果i = 13时, len = 1 + 1+ 1 + 7 就可以得出结果,所需要的前期操作只是把 i=10 时的len值记录保存下来。
这个将重复计算过程值保存下来的思路,被称为记忆化。
总结:
1)将中间的计算结果保存下来,减少后续计算中的重复计算;
2)这种技巧常常被用在搜索算法中,称为“记忆化搜索”。
例如:
先前计算:10 5
16
8
4
2
1
记忆化:f(10) = 7, f(5) = 6, f(16) = 5, ... f(1) = 1;
之后计算:13 40
20
10
5
16
8
4
2
1
直接得到:f(20) = 1+f(10) = 1+7 = 8; f(40) = 1+1+f(10) = 9, f(13) = 1+1+1+f(10) = 10, 少做了6次计算。
- 代码优化思路:
1. 定义一个数据结构 int keep[M] , 用于存储数据范围M之内的序列长度, 即keep[i] = i 的序列长度,(i<M);
2. 当遍历值 n < M 时, len(n) = keep[n];
3. 当遍历值 n > M 时,len(n) = 1+1+ ... + len(i) ; i<M;
- 代码优化实现:
//代码段4
#include <stdio.h>#define MAX_N 1000000
#define MAX_M 10000int keep[MAX_M+5] = {0};int cal_len(long long n){if(n == 1) return 1;if(n <= MAX_M && keep[n]) return keep[n];int ret = ((n & 1) ? cal_len(3*n+1):cal_len(n>>1))+1;if(n <= MAX_M) return keep[n];return ret;
}int main(){int ans = 0, len = 0;for(int i = 1;i< MAX_N;i++){int temp_len = cal_len(i);if(temp_len <= len) continue;ans = i;len = temp_len;}printf("ans = %d, len = %d\n",ans, len);return 0;
}运行结果:

通过计算结果,运行时间果然是缩短了, 目前代码中的keep数组大小是10000,现在将数据规模增加到1000万,keep数据的大小不变:
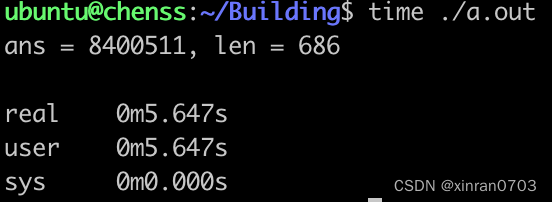
可以看到运行时间原来的约13秒提高到约5秒。
- 优化结果分析
那么keep数组的大小设计为多大合适,是不是越大越好呢?
设: MAX_N = 100 0000
测试1: MAX_M = 10 0000

运行时间由 0.367s 提高到 0.164 s
测试2:MAX_M = 100 0000

运行时间由0.164s 提高到0.032s
测试3:MAX _M = 1000 0000
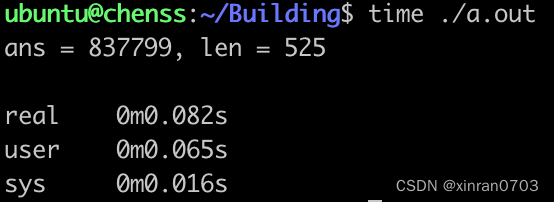
运行时间由0.032s 增加到 0.082s
结论:
增加keep数组的大小是可以提高程序的运行时间的,但keep数组不是越大越好,因为keep是用于搜索查询的,而数据在计算机中是按页存储的,,如果keep数组太大,那么将会开辟多个页用于存储数据,在搜素查询所需数据时,就会将时间用在页面切换上,反而增加了时间的开销。
- 题目总结:
1. 在题目中出现迭代,我们可以考虑递归思想的应用;
2. "segmentation fault" 报错的原因分析。
3. 当出现大量重复计算的时候,考虑“记忆化” 这个优化技巧。
这篇关于最长考拉兹序列的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





