如何理解广角镜头和长焦镜头的区别。

本文主要是介绍如何理解广角镜头和长焦镜头的区别。，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

为什么广角镜头的视野会比长焦镜头的视野大呢？

我之前用等光程解释了景深，也解释了为什么焦距越远，成像越大，但是从来没有提到过视野范围这个概念。实际上在我之前建立的数学模型中，物曲面S是无限大的，像曲面S1也是无限大的。但是实际的照相机中，照片是被框住了的，也就是像曲面S1的大小是固定的，那么怎样使得在S1固定的情况下，物曲面S尽可能的大呢？

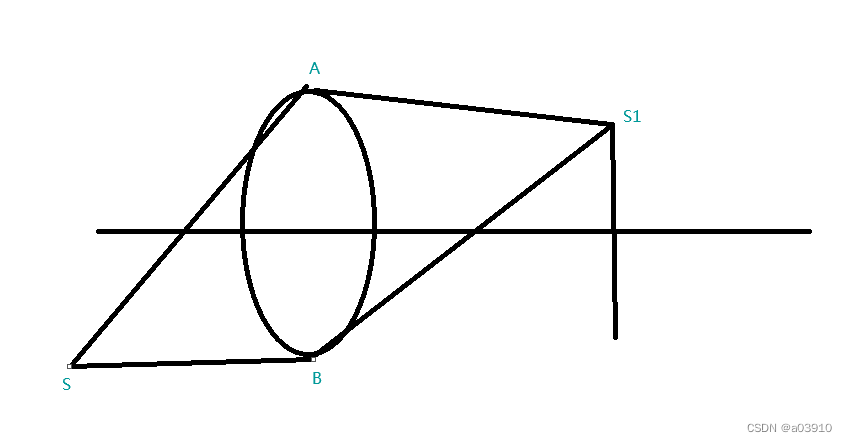
首先，根据费马原理，这是个非常好用的原理，因为可以不用考虑折射，反射，只需要关注问题本身了，譬如这里，从S发出的光在透镜中发生了折射，但是由于折射只是最小光程的结果，光线的路径可以是任意的，那么我随意画，只要等光程即可，反正最后是选择其中光程最小的路径即可，而且这种任意性使得最小光程也符合我从任意的情况下总结出的一般性的规律。

首先有SA+SB=AS1+BS1。

所以就是SA-SB=常数2a，那么S的路径就是个双曲线了，AB的光程2c，(+-c,0)是双曲线的焦点。

注意，这里面，SA和SB是空气的光程，AB是介质中的光程，不一样。A和B是透镜的边界点。

首先假设SA-SB=2a, 可以画出来双曲线如图所示:

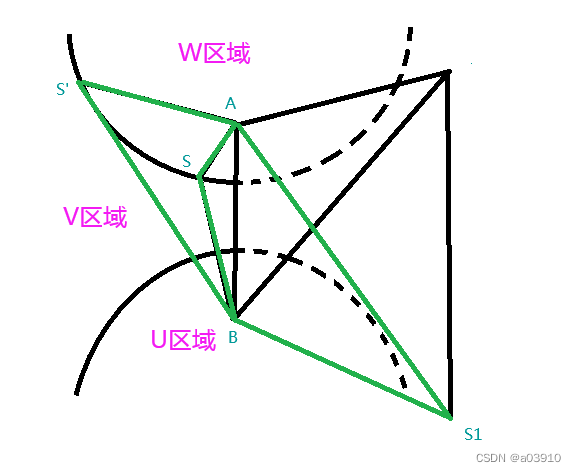
所以到达S1曲面的边界的位置的像点分布在双曲线上，如果是W区域和U区域发出的光呢？比如S'A-S'B大于AB了，那么就会需要像曲面S1更大或者更靠前才能使得像边界点到A和B的光程差变大。而如果是在V区域的点，由于光程差S'A-S'B变小，只要把到像边界位置的点向光轴靠近，就可以缩小光程差了。

所以可以总结出来，透镜左边的物区域，只有V区域包含双曲线的位置是可以在固定大小的成像曲面S1上的。

但是有个问题，我右边给出的是成像曲面是2维度的，左边却是空间区域是3维度的，维度不一样啊。所以，左边的双曲线中，S'点被S点遮挡住了？这还真是个问题，因为右边的光程路径是一样的，但是光线并没有被遮挡，如果改变光圈AB大小，比如缩小AB，那么S'和S在像曲面S中的位置都向光轴靠拢，但是S的光程差改变较大，所以S在像S1中的位置更向光轴靠拢。

物S'和S的最小光程在像曲面S中的位置可能不同，这只是某个光线路径的光程相同，并一定是像点。

首先我给出像点的定义：所谓的像点就是到达这个点的所有的光程都相等，如果只是部分光程相等，那就不是像点。

然后我给出最小光程的解释：最小光程说的是折射的意思。如果所有的光程在像曲面S1上的某个点都相等，那所有的光程都是最小光程了。

但是从最坏的情况考虑，假设双曲线上的物点S'和S的所有光程都在像曲面上，并且最小光程的像点在像曲面S的位置是一样的。那么可以认为这个双曲线是不成像的，因为光线重合了。也就是说在成像的边界处是不成像的，只能感受到有光，但是没有信息。

这个最坏的情况就是成像的视野了。我现在解决透镜右边像曲面是2维的，左边物区域是三维的问题。

实际上同胚的只能是二维的，也就是说能清晰看到的是二维流形，其余的三维的是不清晰的。也就是说在V区域只表示能看到的，但是在任何情况下，能够清晰成像的都是二维的流形，比如三维空间中的球面是二维的。在最小光程双曲线上，W和U区域包括双曲线是不可见的，但是W区域是不在成像曲面S上。而双曲线上是在成像曲面S的边界上，但只是能感受到光而没有信息。

所以，广角镜头为什么周围会有扭曲感呢？就是因为这个不可见的双曲线。

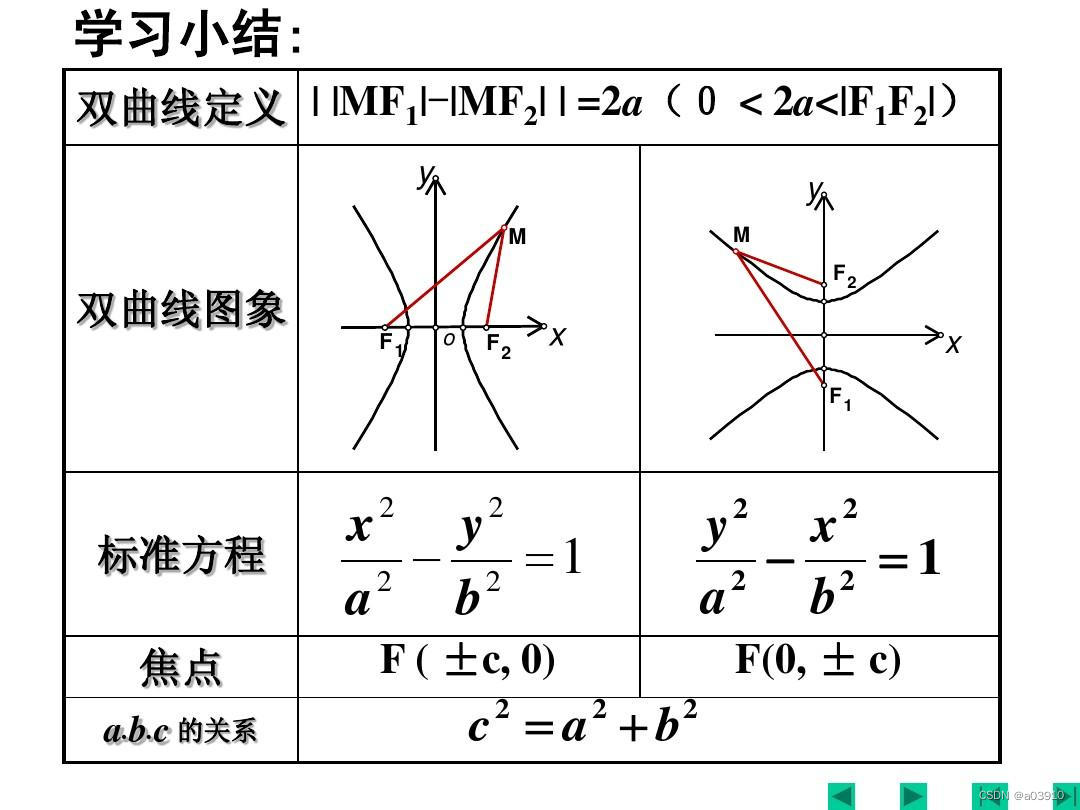当透镜大小，即光程AB=2c不变的时候，而当焦距变小的时候，像曲面S1的距离变小了，即是SA-SB=2a变大了。