本文主要是介绍LeetCode-042-接雨水,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目地址: https://leetcode-cn.com/problems/trapping-rain-water
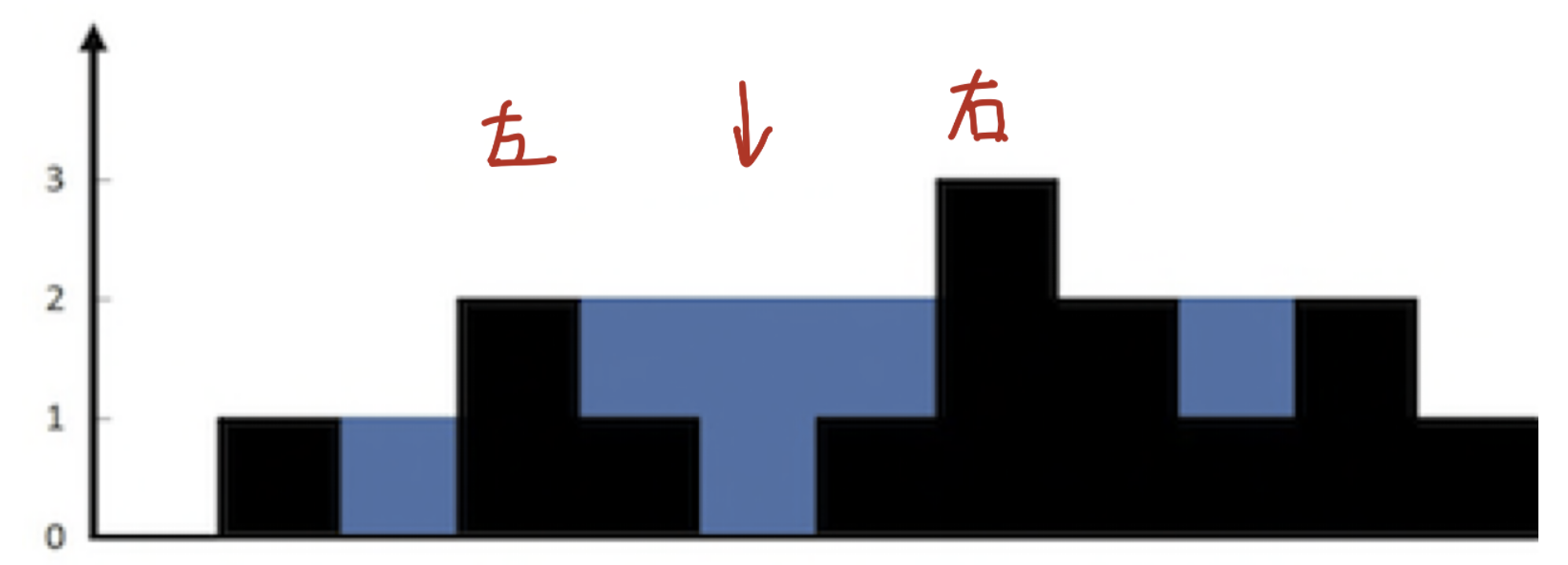
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
第一种方法是暴力求解,对于给定的一个柱子,我们分别找到它的左右边界,然后其中的最小值减除当前柱子的高度,就是它能接的水
int min(int a, int b){return a > b ? b : a;
}int max(int a, int b){return a < b ? b : a;
}int trap(int* height, int heightSize){int left_max;int right_max;int ans=0;//从1到n-1即可,因为第一个和最后一个不能有水for (int i = 1; i < heightSize - 1; i++){left_max = height[i];right_max = height[i];for (int j = 0; j < i; j++){left_max = max(left_max, height[j]);}for (int j = heightSize - 1; j > i; j--){right_max = max(right_max, height[j]);}//计算接水面积ans += min(left_max, right_max) - height[i];}return ans;}这一种方法是两层循环,时间复杂度是O(n^2). 其中第二层的循环是实时计算当前柱子的左右边界。如果已知每个柱子的左右边界,我们就可以省掉嵌套循环,可以用ans += min(left_max[i], right_max[i]) - height[i];直接计算面积。问题就在于如何提前计算好left_max[i]和right_max[i]。我们只需要分别为左右遍历数组,在遍历过程中,比较当前值和前一个值,用其中较大值更新当前值。
class Solution {
public:int trap(vector<int>& height){if(height.size() == 0) return 0;int ans = 0;int size = height.size();vector<int> left_max(size), right_max(size);left_max[0] = height[0];for (int i = 1; i < size; i++) {left_max[i] = max(height[i], left_max[i - 1]);}right_max[size - 1] = height[size - 1];for (int i = size - 2; i >= 0; i--) {right_max[i] = max(height[i], right_max[i + 1]);}for (int i = 1; i < size - 1; i++) {ans += min(left_max[i], right_max[i]) - height[i];}return ans;}};这里用了2个额外的数组,避免了嵌套循环,用空间换时间。
方法3,前面是按列计算每一列的接水量,我们其实还可以按行计算每一行的接水量。
我们依次遍历柱子,如果当前柱子比之前的小,那就说明它有可能和之前的柱子组成一个凹型空间,也就是说它的左边界就是它的前一个柱子,但是右边界我们暂时不清楚。如果当前柱子比上一个元素大,就说明前一个元素的右边界确定了。下面是两个特殊的例子,下图左直到第五个柱子才确定了第四根柱子的左右边界,而下图右则到头都没有找到有边界
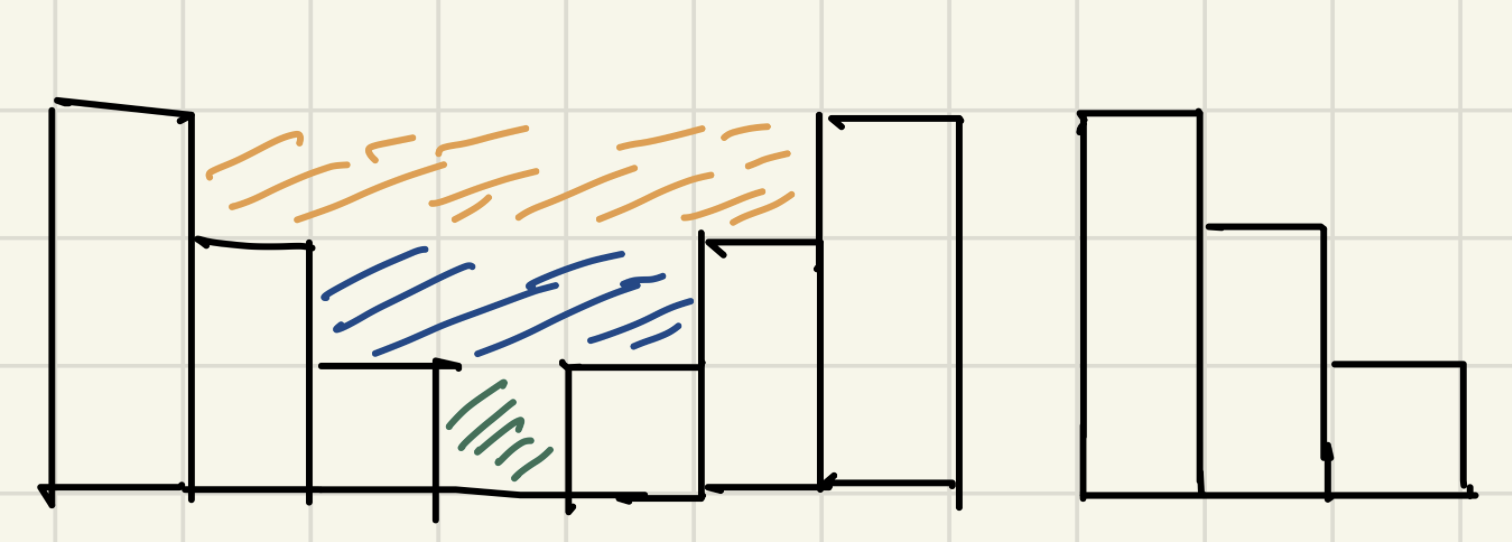
这种依次加入元素,然后从后往前取出元素的方式可以让我们联想到 栈这种先进后出数据结构。具体算法逻辑如下
- 读取最新元素,
- 和栈顶元素对应的高度比较,
- 如果低于栈顶元素对应高度,则直接入栈
- 如果高于栈顶元素对应高度,则开始计算面积
面积的计算公式为,凹型区间两边柱子的较低者减去凹形区间最低元素高度,乘以两边柱子的距离。
代码如下:
class Solution {
public:int trap(vector<int>& height) {int ans = 0;stack<int> st;int current = 0;while( current < height.size()){while( !st.empty() && height[current] > height[st.top()]){//获取中间位置int mid = st.top();st.pop();//获取左侧位置if ( st.empty()) {break;}int left = st.top();//左右间距int distance = current - left - 1;//面积=高度差 x 距离int bound_height = min(height[left], height[current] ) - height[mid];ans += distance * bound_height;}st.push(current++);}return ans;}
};这篇关于LeetCode-042-接雨水的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







