「LeetCode 084」最大面积

本文主要是介绍「LeetCode 084」最大面积，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目地址: https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

example

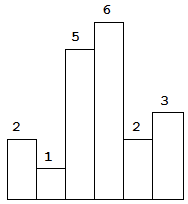
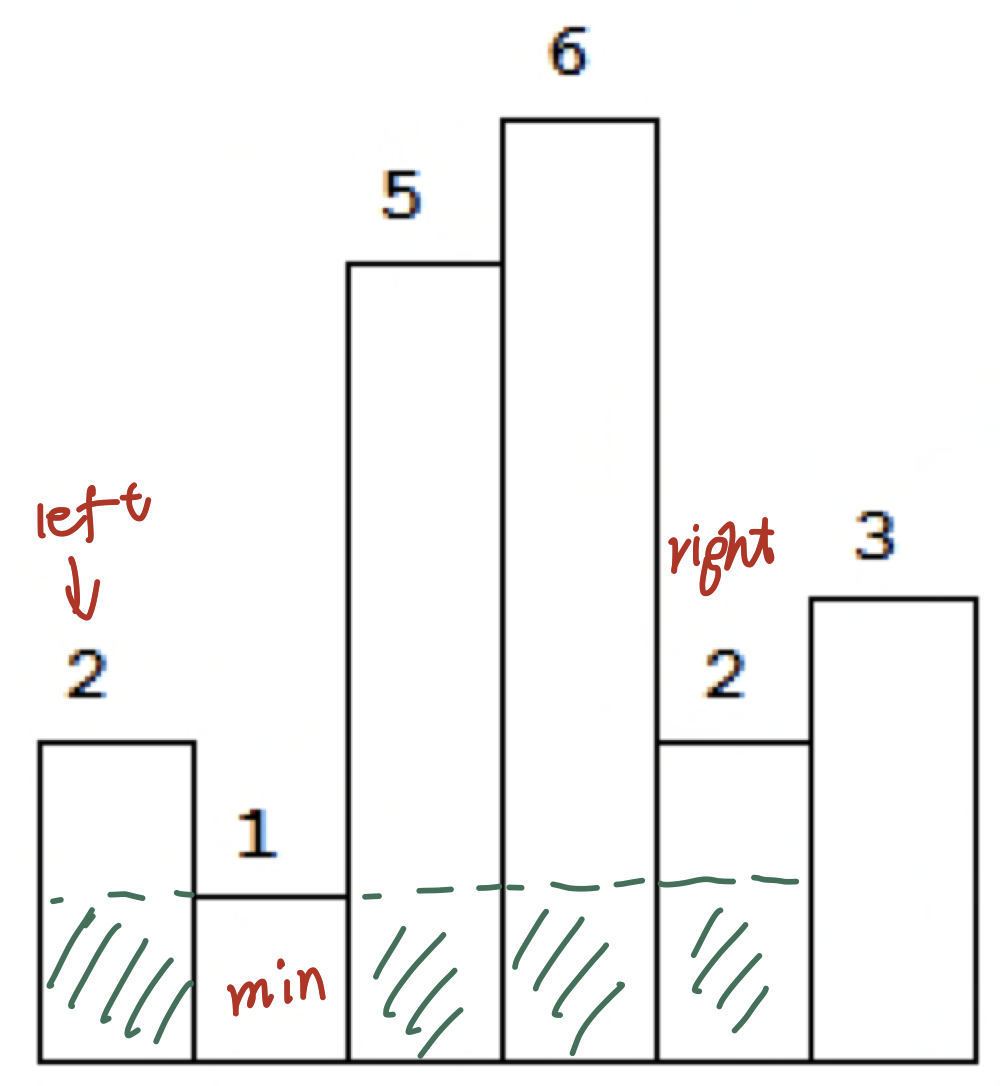
第一种方法，我们先确定左右两个边界，然后找边界中的最小值。比方说，我们左边界确定为(0,2)，右边界确定为(4,2), 然后遍历中间元素，发现最小值是(1,1)，那么面积就是(4-0) x 2 = 8

方法1

代码如下

int min(int a, int b){return a > b ? b : a;
}
int max(int a, int b){return a > b ? a: b;
}int largestRectangleArea(int* heights, int heightsSize){int max_area = 0;for (int i = 0; i < heightsSize; i++){int min_height = heights[i];for (int j = i; j < heightsSize; j++){//找到i-j中的最小高度for ( int k = i; k <= j; k++){min_height = min(min_height, heights[k]);}//计算面积max_area = max(max_area, (j-i+1) * min_height);}}return max_area;}

我写代码时出错的两个地方

是k <= j而不是k<j, 要包括最后一个位置。
面积的计算公式为(j-i+1) * min_height, 我漏了+1，结果(0,1)我算成了0，而实际面积是(0-0+1)x1=1

上面方法是固定左右边界然后找中间的最小值，用到了三层循环，计算效率比较低。我们可以想办法省掉第三层循环，比如说当我们计算完(0,2)-(2,5)内的最小值后，对于(0,2)-(3,6)的最小值，其实只要比较当前高度和之前的最小值，如果比前面的小，就更新最小值，否则就用之前的最小值。代码如下

int largestRectangleArea(int* heights, int heightsSize){int min_height = 0;int max_area = 0;for ( int i = 0 ; i < heightsSize; i++){min_height = heights[i];for ( int j = i ; j < heightsSize; j++){min_height = min(min_height, heights[j]);max_area = max(max_area, (j-i+1) * min_height);}}return  max_area;}

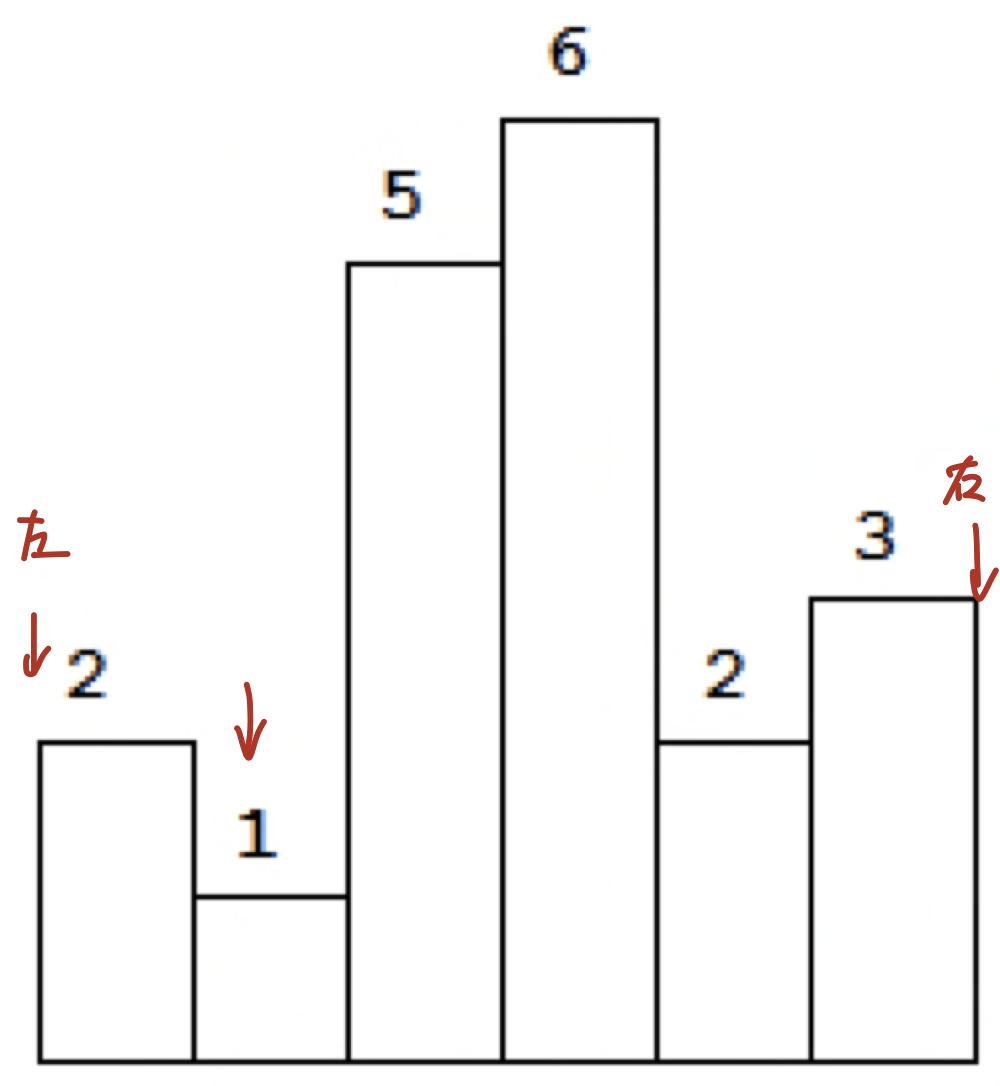
或者我们可以换个思路，先把中间值固定住，然后找左右边界。这里的边界指的是左右出现的第一个比他小的棒子，比如说(1,1)就是最两边。

方法2

代码如下

int largestRectangleArea(int* heights, int heightsSize){int max_area = 0;for ( int i = 0; i < heightsSize; i++){int left_border = 0;int right_border = heightsSize;for (int j = i; j < heightsSize; j++){if (heights[j] < heights[i]){right_border = j;break;}}for (int j = i; j >= 0; j--){if (heights[j] < heights[i]){left_border = j+1;break;}}max_area = max(max_area, (right_border-left_border) * heights[i]);}return max_area;}

依旧需要两层循环，其中第二层循环的目的是就是找到左右边界。那有没有方法不需要用到循环就能找到左右的边界呢？

思路和第二种方法类似，通过记录已经出现的最小值来避免多余计算，只不过这里用栈处理，具体步骤为

栈初始化，入栈-1
对于每一个新元素，都和栈顶元素比较
如果比栈顶元素大
- 该元素就入栈
如果比栈顶元素小
- 先取出栈顶元素，计算栈顶元素对应的面积
- 重复上面步骤，直到比栈顶元素大
- 入栈
遍历结束后，清空栈

我们以最特殊的两个数据来举例，对于[0,1,2,3,4,5,6,7], 每一个元素都比之前的小，那么每个元素入栈的时候，我们都只能确定它的左边界，也就是它的上一个元素，而无法确定它的右边界，比如说(1,1)的左边界就是(0,0), 而右边的位置必须等到所有元素都入栈之后才能确定，最后算出来的面积是(8-1)x1=7.

方法3-1

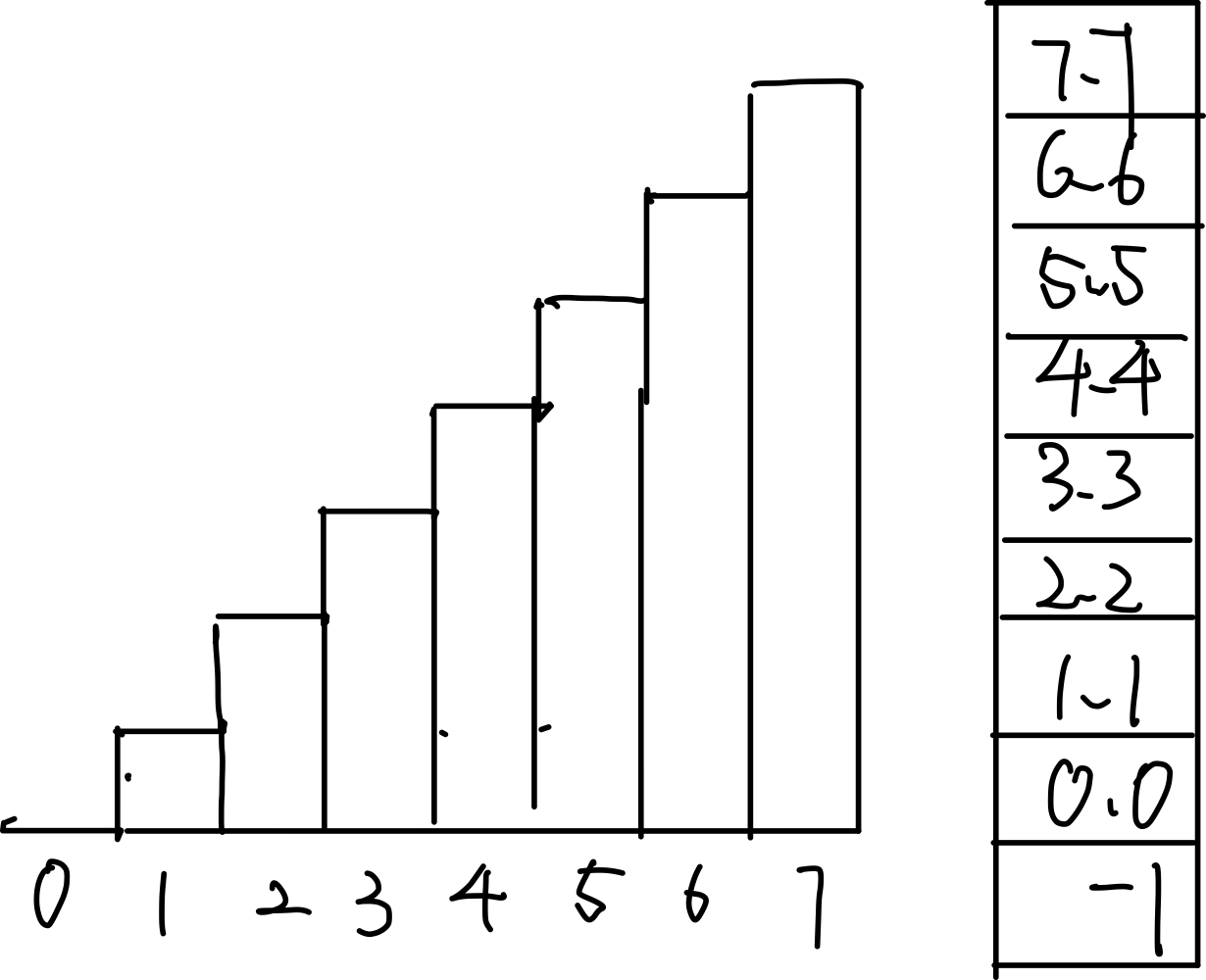
对于[7,6,5,4,3,2,1,0], 我们先入栈(0,7)，然后入栈(1,6), 此时对于高度为7的棒子而言，它已经到头了，面积只肯能是7. 一波操作之后，栈内部元素为(1,6), 此时来了(2,5), 那么6也到头了，它的面积就是(1-(-1) x 6 = 12.，其中-1栈初始后第一个元素。

最终代码如下（大部分代码是实现栈的操作）

int max(int a, int b){return a > b ? a : b;
}typedef struct {int *arr;int count;
} Stack;Stack *create(int k){Stack *st = malloc(sizeof(Stack));st->arr = malloc(sizeof(int) * (k+2));st->count = 0;return st;
}void push(Stack *st, int val){st->arr[st->count] = val;st->count++;return ;
}int peek(Stack *st){return st->arr[st->count-1];}
int pop(Stack *st){st->count--;return st->arr[st->count];
}void destroy(Stack *st){free(st->arr);free(st);return;
}int largestRectangleArea(int* heights, int heightsSize){Stack *st = create(heightsSize);push(st, -1);int max_area = 0;for (int i = 0; i < heightsSize; i++){//如果不为空，且当前元素小于栈顶元素while (  && heights[i] < heights[peek(st)]){max_area = max(max_area, heights[pop(st)] *( i -  peek(st)-1 )) ;}push(st, i);}while ( peek(st) != -1){max_area = max(max_area, heights[pop(st)] *( heightsSize -  peek(st) - 1) );}destroy(st);return max_area;
}

我写代码出错的两个地方