第二章 通信信道

本文主要是介绍第二章 通信信道，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第二章 通信信道

通信信道的定义和分类

• 信道：以传输媒介(质)为基础的信号通路。

• 信道的作用是传输信号

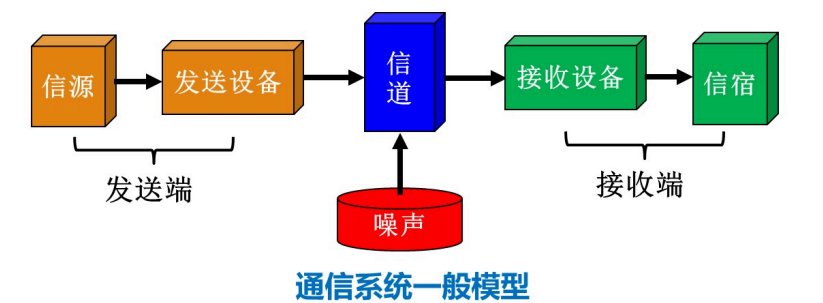
狭义信道：有线信道、无线信道

广义信道：调制信道（模拟通信系统）、编码信道（数字通信系统）

• 通信信道的定义：从信号与系统的角度研究信道的特性

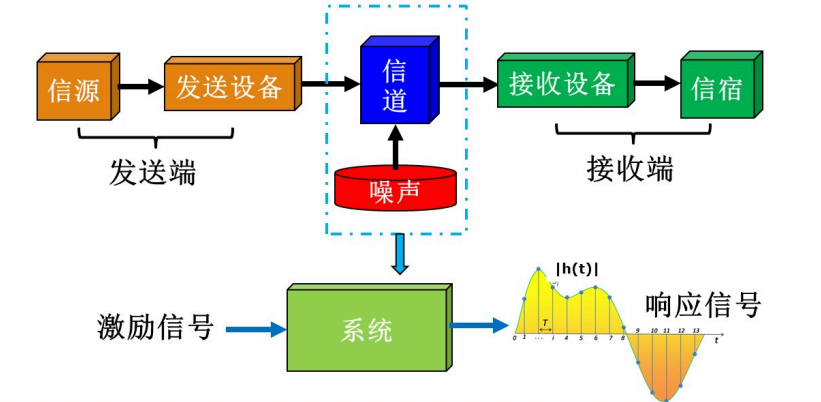
信道通信模型

通信信道模型:调制信道

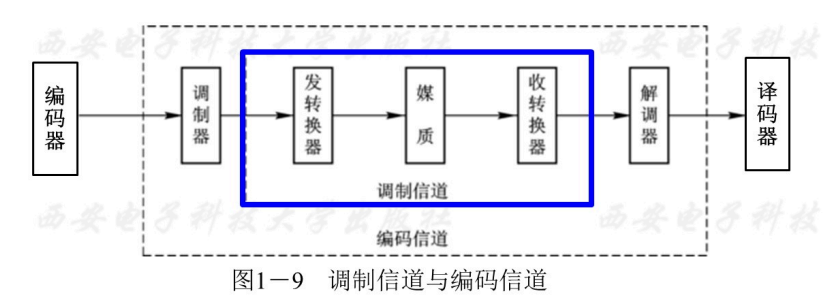
• 调制信道：从调制器的输出端到解调器的输入端。

1. 有一对(或多对)输入端，则必然有一对(或多对)输出端；
2. 绝大部分信道是线性的，即满足叠加原理；
3. 信号通过信道需要一定的迟延时间；
4. 信道对信号有损耗(固定损耗或时变损耗)；
5. 即使没有信号输入，在信道的输出端仍可能有一定的功率输出(噪声)。

二对端调制信道模型

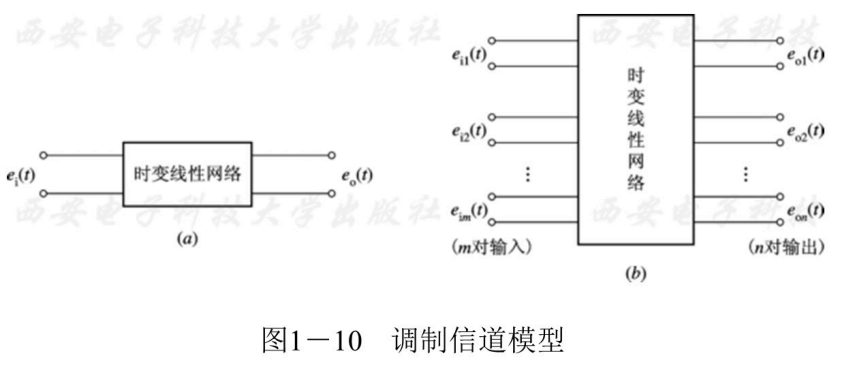
• 对于二对端的信道模型来说，它的输入和输出之间的关系式可表示成：
  $$\begin{gathered} e_o(t)=f[e_i(t)]+n(t) \\ f[e_i(t)]为信道对信号影响(变换)的某种函数关系 \\ {e}_o(t)=k(t)\cdot e_i(t)+n(t) \\ k(t):乘性干扰n(t):加性干扰 \end{gathered}$$

  • 加性干扰n(t):可以人为造成，或者外界环境噪声
  • 乘性干扰k(t): 复杂函数，包括线性畸变、非线性失真、时间延迟及衰减等；随时间变化的特性

---

• 调制信道分类：

  • 恒参信道：k(t)不随时间t变化或变化极为缓慢，有线信道、卫星信道、微波链路可被看成恒参信道。

  • 随参信道：k(t)随时间t随机变化，移动无线信道为随参信道。

• k(t)，它依赖于网络的特性，对信号e;(t)影响较大。理想信道直应是k(t)=常数，$n(t)=0$，即：$$e_0(t)=k\cdot e;(t)$$

通信信道模型：编码信道

• 编码信道：从编码器的输出端到译码器的输入端

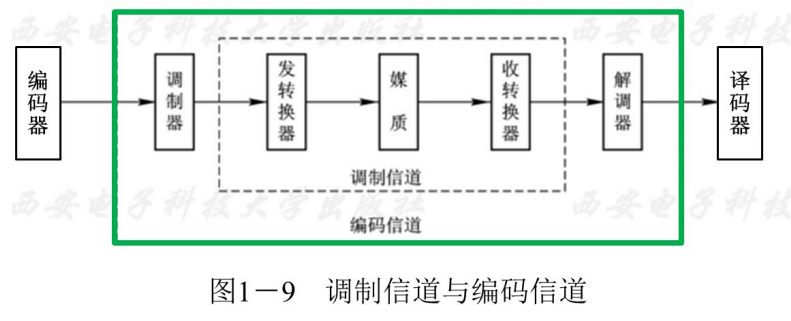
• 编码信道(数字信道)主要特性：
  1. 包括调制器、解调器、发送变换器及传输媒介；
  2. 对信号的影响是数字序列的变换：
  3. 调制信道不理想会导致编码信道产生错码；
  4. 调制信道越差，发生错误的概率越大
• 编码信道的模型可用数字信号信道转移概率来描述。

---

• 例：最常见的二进制数字传输系统中，假设解调器输出的每个数字码元发生差错是相互独立的，则一个简单的编码信道模型可表示如图所示：

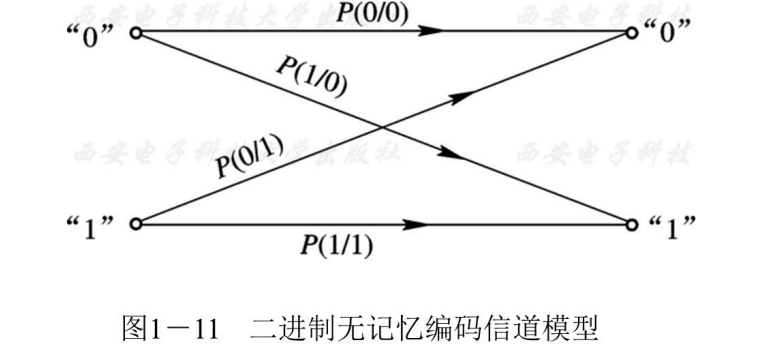
• 在这个模型里，把P(0/0)、P(1/0)、P(0/1)、P(1/1)称为信道转移概率

  • 正确转移概率：P(0/0)和P(1/1)
  • 错误转移概率：P(1/0)和P(0/1)

• 根据概率性质可知:
  $$\begin{gathered} P(0/0)+P(1/0)=1 \\ P(1/1)+P(0/1)=1 \end{gathered}$$

信道噪声和干扰

• 有害电信号，叠加在信号上，淹没或模糊了有用信号，限制接收机正确判断码元的能力，从而限制信息的传输速率。

• 通常将加性噪声n(t)分为自然噪声和人为干扰，它们降低了接收信号的信干比，从而影响接收机的正常工作，导致模拟通信产生失真，数字通信产生误码。

• 噪声的来源：

  • 自然噪声：包括自然界辐射的噪声和接收机内部的热噪声。
  • 热噪声：任何温度高于绝对零度的电子设备所固有的，来自电阻性元器件中电子的热运动，是典型的高斯白噪声。

• 噪声的分类：

  • 自然噪声：银河噪声、大气噪声、降雨噪声、地面噪声等
  • 热噪声：电子导体噪声、火花塞点火噪声、开关噪声、其他电磁辐射噪声等。

• 高斯噪声：概率密度函数服从高斯分布(即正态分布)。高斯噪声的一维概率密度函数表示为：
  

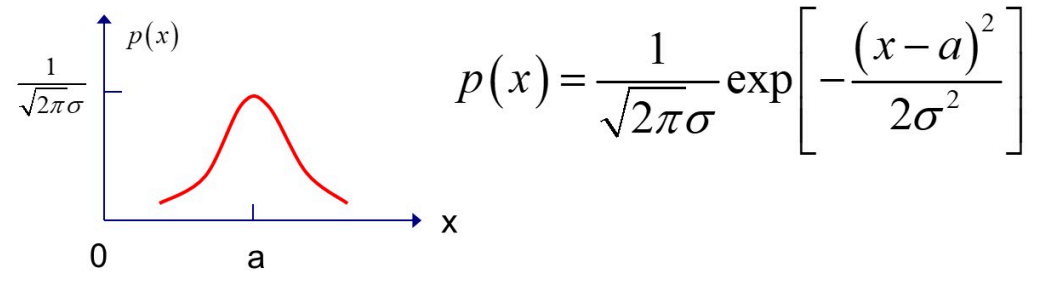
  • 当噪声均值a=0为零时，噪声的平均功率等于噪声的方差，即:
    $$P_n={\sigma }^2$$

• 白噪声：率谱密度函数在整个频域范围内是常数，即功率谱密度函数在频域内均匀分布

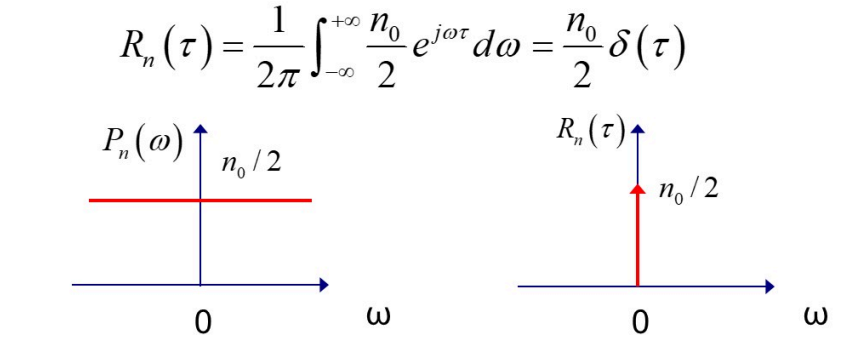
• 高斯白噪声口高斯白噪声，是指噪声的概率密度函数满足正态分布统计特性，其功率谱密度函数是常数。

• 典型的高斯型白噪声——热噪声

• 高斯型白噪声同时涉及到噪声的两个不同方面，即概率密度函数的正态分布性和功率谱密度函数均匀性，二者缺一不可。

---

• 信道中的干扰：己方和民用设备造成的干扰；敌方施放的恶意干扰。

信道容量

• 信道容量：月用于衡量物理信道能够传输数据的最大能力的基本标准，常以单位时间内信道中信息能够无差错传输的最大平均信息速率表征。
• 信道容量分类：连续信道(模拟通信系统)、离离散信道(数字通信系统)

香农公式

• 对连续信道(或调制信道)的输入端加入带宽有限、平均功率有限的谱密度为$n_o(W/Hz)$的加性高斯白噪声。设信道的带宽为$B(Hz)$，信号功率为$S(W)$，则通过这种信道无差错传输的最大信息速率$C$

$$\begin{gathered} C=Blo{g}_2(1+\frac{S}{N_{0}B})(b/s) \\ [n_{0}B是噪声的功率，令N=n_{0}B] \\ C=Blo{g}_2(1+\frac{S}{N})(b/s) \end{gathered}$$

• 结论：

1. 任何一个连续信道都有信道容量。在给定B、S/N的情况下，信道的极限传输能力为C。
   • 如果信源的信息速率R小于或等于信道容量C，那么在理论上存在一种方法使信源的输出能以任意小的差错概率通过信道传输；
   • 如果R大于C，则无差错传输在理论上是不可能的。因此，实际传输速率(一般地)要求不能大于信道容量，除非允许存在一定的差错率。
2. 增大信道容量C

3. 当信道容量保持不变时，信道带宽B、信号噪声功率比S/N及传输时间三者是可以互换的。若增加信道带宽，可以换来信号噪声功率比的降低，反之亦然。如果信号噪声功率比不变，那么增加信道带宽可以换取传输时间的减少，反之亦然。

   • 当信道容量C给定时，B1、S/N,和B2、S2/N2分别表示互换前后的带宽和信号噪声比，则有

   $$B_{1}lb(1+\frac{S_1}{N_1})=B_{2}lb(1+\frac{S_2}{N_2})$$

离散信道容量

• 广义信道中的编码信道就是一种离散信道，常用转移概率描述。
  • 设 $P(x_i)$表示信源发送符号$x_i$的概率
  • $P(y_i)$表示接收端收到$y_i$,的概率;
  • $P(x_i|y_i)$表示在发送$x_i$, 的条件下收到$y_i$的条件概率,也称转移概率。

这篇关于第二章 通信信道的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---