本文主要是介绍某神的算法[uf,ab,ef]相关算法浅谈,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!



以上java层调用过程图
so 是做了处理的
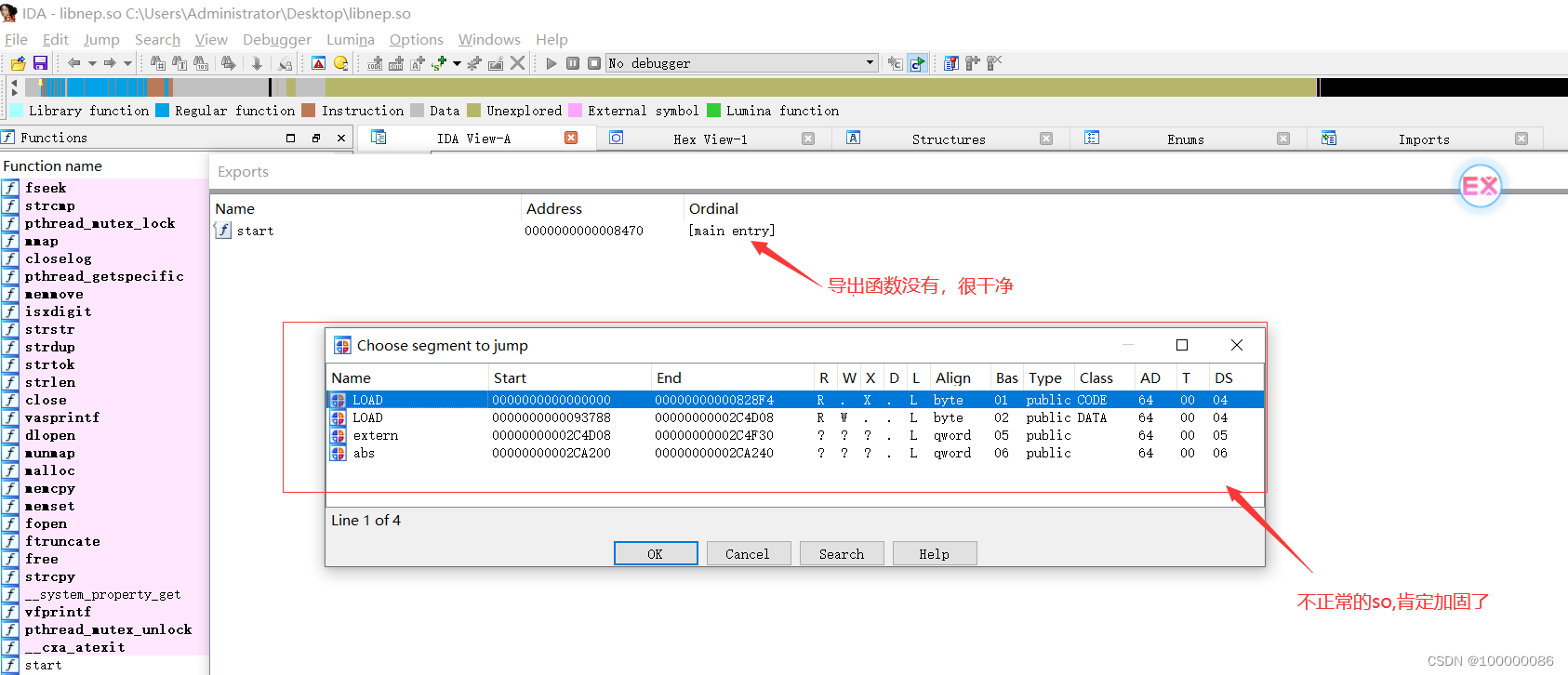
导出函数没有,说明是加固了。那就要内存解析后dump出解密的so.不能无法分析

jstring __fastcall Java_com_netease_nep_Tools_getPostMethodSignatures(JNIEnv *a1,__int64 a2,__int64 a3,__int64 a4,__int64 a5,__int64 a6,__int64 a7,__int64 a8,__int128 a9,__int128 a10,std::exception *a11,__int128 a12,std::exception *a13,__int16 a14,__int64 a15,std::exception *a16,__int128 a17,std::exception *a18,__int64 a19,__int64 a20,std::exception *a21,__int128 a22,std::exception *a23,__int64 a24,__int64 *a25,__int64 a26,__int64 a27,__int64 a28,__int128 *a29,__int64 a30)
{int v35; // w24unsigned int i; // w25jobject v37; // x27jobject v38; // x0void *v39; // x28__int64 v40; // x0jstring result; // x0__int64 v42; // x20std::exception *v43; // x21std::exception *v44; // x23unsigned __int64 v45; // x22unsigned int v47; // w9__int64 v48; // x20std::exception *v49; // x21std::exception *v50; // x23unsigned __int64 v51; // x22unsigned int v53; // w9std::exception *v54; // x1jstring v55; // x19__int64 v56; // x19__int64 v57; // x0__int64 v58; // x1__int64 v59; // x2__int64 v60; // x3__int64 v61; // x4a30 = *(_ReadStatusReg(ARM64_SYSREG(3, 3, 13, 0, 2)) + 40);if ( !a3 ){result = ((*a1)->NewStringUTF)(a1, &unk_28405C, 0LL, a4, a5, a6, a7, a8);if ( *(_ReadStatusReg(ARM64_SYSREG(3, 3, 13, 0, 2)) + 40) == a30 )return result;
LABEL_67:sub_1C82C0(result);goto LABEL_68;}a26 = 0LL;a27 = 0LL;a25 = &a26;if ( a5 ){if ( a6 ){v35 = (*a1)->GetArrayLength(a1, a6);if ( v35 == (*a1)->GetArrayLength(a1, a5) && v35 >= 1 ){for ( i = 0; i < v35; ++i ){v37 = (*a1)->GetObjectArrayElement(a1, a5, i);v38 = (*a1)->GetObjectArrayElement(a1, a6, i);v39 = v38;if ( v37 && v38 ){sub_2004BC(a1, v37);sub_2004BC(a1, v39);a29 = &a22;v40 = sub_201194(&a25, &a22, 2625040LL, &a29, &a28);sub_1E97EC(v40 + 56, &a19);(*a1)->DeleteLocalRef(a1, v37);(*a1)->DeleteLocalRef(a1, v39);if ( (a19 & 1) != 0 )std::exception::~exception(a21);if ( (a22 & 1) != 0 )std::exception::~exception(a23);}}}}}sub_2004BC(a1, a3);a23 = 0LL;a22 = 0uLL;if ( a4 ){sub_2004BC(a1, a4);if ( (a22 & 1) != 0 ){*a23 = 0;*(&a22 + 1) = 0LL;}else{LOWORD(a22) = 0;}sub_1C9E60(&a22, 0LL);a23 = a21;a22 = *&a19;}a13 = 0LL;a12 = 0uLL;if ( (a17 & 1) == 0 ){a13 = a18;a12 = a17;goto LABEL_36;}v42 = *(&a17 + 1);if ( *(&a17 + 1) >= 0xFFFFFFFFFFFFFFF0LL ){
LABEL_68:sub_1CA15C(&a12);goto LABEL_69;}v43 = a18;if ( *(&a17 + 1) > 0x16uLL ){v45 = (*(&a17 + 1) + 16LL) & 0xFFFFFFFFFFFFFFF0LL;while ( !__ldxr(&dword_2C31D8) ){if ( !__stxr(1u, &dword_2C31D8) ){aAllocatorTAllo_5[64] ^= 0x4Bu;*aAllocatorTAllo_5 = veorq_s8(*aAllocatorTAllo_5, unk_280D90);*&aAllocatorTAllo_5[16] = veorq_s8(*&aAllocatorTAllo_5[16], unk_280DA0);aAllocatorTAllo_5[65] ^= 0x5Cu;aAllocatorTAllo_5[66] ^= 0xCAu;*&aAllocatorTAllo_5[32] = veorq_s8(*&aAllocatorTAllo_5[32], unk_280DB0);*&aAllocatorTAllo_5[48] = veorq_s8(*&aAllocatorTAllo_5[48], unk_280DC0);aAllocatorTAllo_5[67] ^= 0xDAu;atomic_store(2u, &dword_2C31D8);goto LABEL_33;}}__clrex();dov47 = atomic_load(&dword_2C31D8);while ( v47 != 2 );
LABEL_33:v44 = operator new[]((v42 + 16) & 0xFFFFFFFFFFFFFFF0LL);*(&a12 + 1) = v42;a13 = v44;*&a12 = v45 | 1;if ( !v42 )goto LABEL_35;}else{LOBYTE(a12) = 2 * BYTE8(a17);v44 = (&a12 + 1);if ( !*(&a17 + 1) )goto LABEL_35;}sub_1C6E70(v44, v43, v42);
LABEL_35:*(v44 + v42) = 0;
LABEL_36:a11 = 0LL;a10 = 0uLL;if ( (a22 & 1) == 0 ){a11 = a23;a10 = a22;goto LABEL_51;}v48 = *(&a22 + 1);if ( *(&a22 + 1) < 0xFFFFFFFFFFFFFFF0LL ){v49 = a23;if ( *(&a22 + 1) > 0x16uLL ){v51 = (*(&a22 + 1) + 16LL) & 0xFFFFFFFFFFFFFFF0LL;while ( !__ldxr(&dword_2C31D8) ){if ( !__stxr(1u, &dword_2C31D8) ){aAllocatorTAllo_5[64] ^= 0x4Bu;*aAllocatorTAllo_5 = veorq_s8(*aAllocatorTAllo_5, unk_280D90);*&aAllocatorTAllo_5[16] = veorq_s8(*&aAllocatorTAllo_5[16], unk_280DA0);aAllocatorTAllo_5[65] ^= 0x5Cu;aAllocatorTAllo_5[66] ^= 0xCAu;*&aAllocatorTAllo_5[32] = veorq_s8(*&aAllocatorTAllo_5[32], unk_280DB0);*&aAllocatorTAllo_5[48] = veorq_s8(*&aAllocatorTAllo_5[48], unk_280DC0);aAllocatorTAllo_5[67] ^= 0xDAu;atomic_store(2u, &dword_2C31D8);goto LABEL_48;}}__clrex();dov53 = atomic_load(&dword_2C31D8);while ( v53 != 2 );
LABEL_48:v50 = operator new[]((v48 + 16) & 0xFFFFFFFFFFFFFFF0LL);*(&a10 + 1) = v48;a11 = v50;*&a10 = v51 | 1;if ( !v48 )goto LABEL_50;}else{LOBYTE(a10) = 2 * BYTE8(a22);v50 = (&a10 + 1);if ( !*(&a22 + 1) )goto LABEL_50;}sub_1C6E70(v50, v49, v48);
LABEL_50:*(v50 + v48) = 0;
LABEL_51:sub_1C7AB0(&a12, &a10, &a25);if ( (a10 & 1) != 0 )std::exception::~exception(a11);if ( (a12 & 1) != 0 )std::exception::~exception(a13);if ( (a14 & 1) != 0 )v54 = a16;elsev54 = (&a14 + 1);v55 = (*a1)->NewStringUTF(a1, v54);if ( (a14 & 1) != 0 )std::exception::~exception(a16);if ( (a22 & 1) != 0 )std::exception::~exception(a23);if ( (a17 & 1) != 0 )std::exception::~exception(a18);result = sub_1EA500(&a25, a26);if ( *(_ReadStatusReg(ARM64_SYSREG(3, 3, 13, 0, 2)) + 40) == a30 )return v55;goto LABEL_67;}
LABEL_69:v56 = sub_1CA15C(&a10);if ( (a12 & 1) != 0 )std::exception::~exception(a13);if ( (a22 & 1) != 0 )std::exception::~exception(a23);if ( (a17 & 1) != 0 )std::exception::~exception(a18);sub_1EA500(&a25, a26);v57 = sub_27E5B0(v56);return sub_201194(v57, v58, v59, v60, v61);
}代码是能正常看到了,不过很复杂,里面是相互嵌套的,静态搞了很久,不行。原因是采用ollvm
ollvm原理
Ollvm大致可分为 bcf(虚假块), fla(控制流展开), sub(指令膨胀), Split(基本块分割)
bcf:
克隆一个真实块,并随机替换其中的一些指令,然后用一个永远为真的条件建立一个分支。克隆后的块是不会被执行的。
Fla:
将所有的真实块使用一个switch case结构包裹起来,每个真实块执行完毕后都会重新赋值switch var,对于有分支的块会使用select指令,并跳转到switch起始代码块(分发器)上,根据switch var来执行下一个真实块。
Sub:
指令膨胀,将一条运算指令,替换为多条等价的运算指令。
Split:
利用随机数产生分割点,将一个基本块分割为两个,并使用绝对跳转连接起来。
关于ollvm具体的实现,可参考源码。

看着这个是不是吓到了,在这织布呢,通过不断地调试,最后搞定
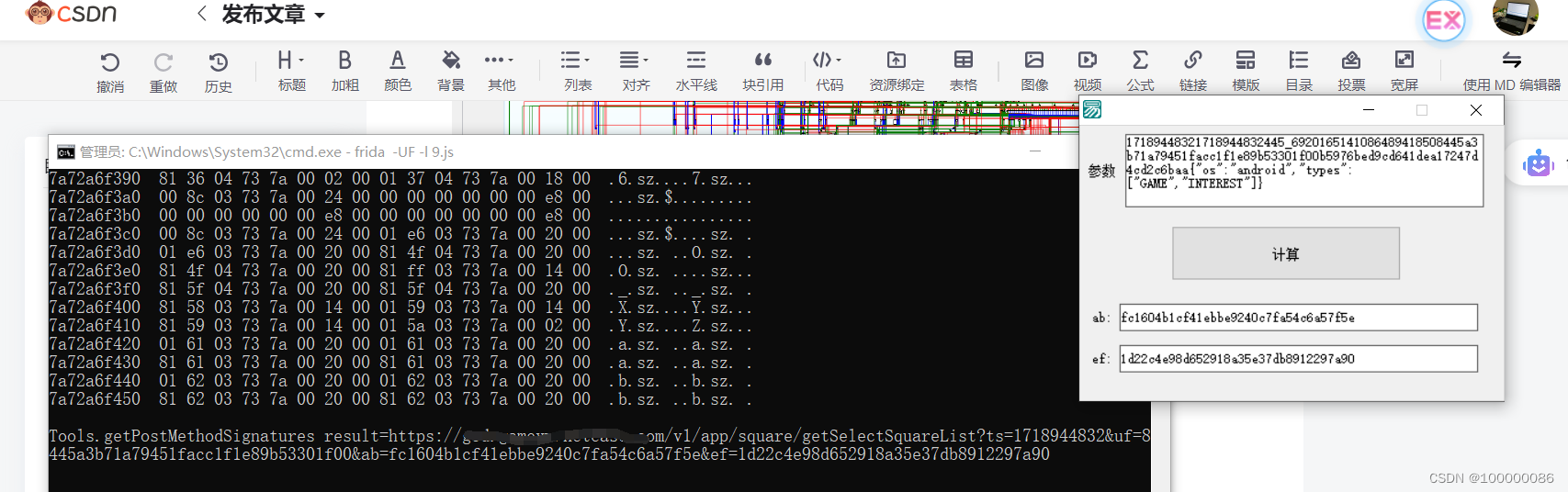
收工
这篇关于某神的算法[uf,ab,ef]相关算法浅谈的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






