本文主要是介绍入门指南-因子分解机及其在大数据集上的应用(含Python代码),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者:ANKIT CHOUDHARY
编译:ronghuaiyang
上回我们对FM的论文原文进行了精读,今天我们就来看一下,究竟如何在实际的数据集上使用FM算法,今天的文章中还提到了FFM算法,是对FM算法的一个改进,我们会在后续的文章中同样对FFM论文进行精读。
今天的文章有算法还有代码,不可错过!
干货开始!
摘要:
我依然记得我第一次遇到点击率预测的问题的时候的情景。在此之前,我学习过数据科学的相关内容,我觉得自己进展的很好。我在机器学习的黑客马拉松上建立了自己的信心,而且在几个挑战赛上表现的也挺好。
为了做的更好,我甚至买了一个16GB的i7的电脑。但是我第一次看到这个数据集的时候,我开始紧张了。整个数据集在解压之前就超过了50G,我对在这个数据集上预测点击率一点头绪也没有,然后因子分解机过来救我了。
所有做点击率预测的人应该都遇到过类似的问题,数据集非常的大,在这么大的数据集上进行预测需要大量的计算资源。
然而在大多数的情况下,数据集是非常稀疏的(每个样本中只有少数几个变量是非0的),由于有一些特征对于预测的关系是不大的,因子分解帮助我们找到每一个样本中最重要的潜在的特征。
因子分解利用低维的稠密的矩阵帮助我们表达目标和预测器之间的相似的关系。本文中,我们讨论了Factorization Machines(FM) 和 Field Aware Factorization Machines(FFM) ,让我们可以利用因子分解的技术来进行回归和分类,并有python的实现。
内容:
1、因子分解背后的直觉
2、因子分解机是如何打败了多项式和线性模型的
3、领域因子分解机
4、使用xLearn的库在python中实现
因子分解背后的直觉
为了直观的理解矩阵的因子分解,我们考虑这样的一个例子,我们有一个用户-电影的评分矩阵,评分范围为1~5.
Star Wars I | Inception | Godfather | The Notebook | |
U1 | 5 | 3 | – | 1 |
U2 | 4 | – | – | 1 |
U3 | 1 | 1 | – | 5 |
U4 | 1 | – | – | 4 |
U5 | – | 1 | 5 | 4 |
我们发现,表格中某些值是缺失的,我们需要设计出一个方法来预测出这些缺失的值。使用矩阵因子分解背后的直觉在于,一定有一些潜在的变量,决定了用户是如何去对一个电影进行评分的。比如说,用户A和B如果都是艾·帕奇诺的粉丝的话,那么他们会对艾·帕奇诺的电影评高分。那么对某个演员的偏好就是一个隐含的特征,而这个特征并没有在评分矩阵中显式的表现出来。
假如我们要找到这个k维的隐含特征,我们需要找到两个矩阵,P(U×K)和Q(D×K),使得P×Q’尽量的接近R,R就是我们的评分矩阵。
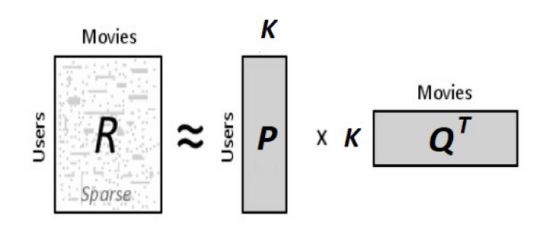
P的每一行表示了每个用户对于这个隐含特征的关系的强度,同样,Q的每一行表示了每个电影对于这个隐含特征的关系的强度。我们可以通过P的每一行和Q的每一行的内积来计算用户对这个电影的评分。
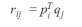
我们现在需要的就是计算这个P和Q,我们通过梯度下降的方式来计算,目标函数就是计算出来的评分和实际的评分之间的均方误差值,我们通过最小化这个目标函数来求解P和Q。均方误差表达式如下:
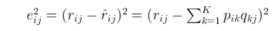
参数的更新方法如下:先计算梯度,再进行参数更新。
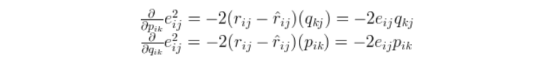
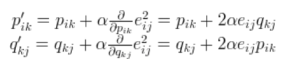
通过上面的更新策略,我们可以进行迭代直到收敛,我们可以通过下面的总的loss来观察,决定什么时候停止更新。
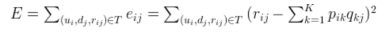
上面这种方法太过简单,通常会过拟合。我们可以在用户特征向量和电影特征向量中分别引入正则化参数来防止过拟合。
如果有人对python的实现感兴趣的,可以查看这个链接link。一旦我们得到P和Q,我们就可以对评分矩阵进行估计。不仅仅是重新估计的原有的评分,还有对原来缺失值的评分。
Star Wars I | Inception | Godfather | The Notebook | |
U1 | 4.97 | 2.98 | 2.18 | 0.98 |
U2 | 3.97 | 2.4 | 1.97 | 0.99 |
U3 | 1.02 | 0.93 | 5.32 | 4.93 |
U4 | 1.00 | 0.85 | 4.59 | 3.93 |
U5 | 1.36 | 1.07 | 4.89 | 4.12 |
因子分解机是如何打败多项式和线性模型的
我们再考虑一个点击率预测的例子,这个数据集将点击率和运动新闻网站和运动品牌进行关联。
Clicked | Publisher (P) | Advertiser (A) | Gender (G) |
Yes | ESPN | Nike | Male |
No | NBC | Adidas | Male |
当我们说FMs和FFM的时候,数据集中的每一列表示一个领域,也就是一个特征。
线性回归和逻辑回归模型在这类任务上有很好的效果,但是缺点在于,只用到了独立的特征,而不是组合的特征。
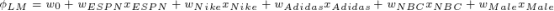
一个利用组合特征的方法就是使用多项式的组合来学习不同变量间的相互关系。
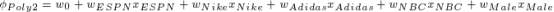
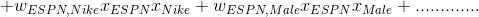
这个是2阶多项式模型,只考虑了特征的两两组合。
对于我们的数据集来说,这个方法有两个问题
l 我们的数据集太大了,需要的内存太多,训练花费的时间也太长
l 我们的数据集太稀疏,没办法学到有效的参数,我们没有足够的非0数据来学习特征组合的参数
FM来救场
FM解决这个问题的时候,考虑到了成对的特征之间的相互关系,让我们可以从成对的特征组合中基于有效的潜在特征进行训练。FM的训练在时间和空间上都是线性复杂度的。可以通过低维的向量的点乘来对成对的特征的相互关系进行建模。下面是2阶时的情况:
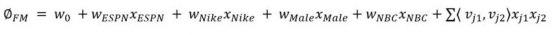
每个参数(k=3)可以表示如下:
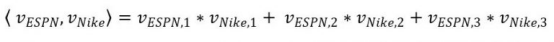
从模型的角度来看,这种方式是非常有效的,每一个特征都被映射到了一个空间中,在这个空间中,相似的特征的距离是相近的。简而言之,内积表示的是两个潜在特征之间的相似性,越大表示越相似。
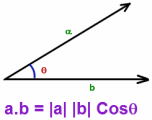
余弦距离表示了相似性,角度是0的时候,最相似,相似性为1,角度是180的时候,相似度为-1。
举例:FM比二阶多项式好的例子
考虑下面的点击率预测的数据
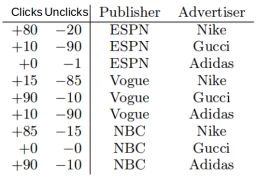
在这个数据集中,有以下两个问题需要注意:
l 数据组合(ESPN, Adidas)只有一个负样本,正样本为0,如果使用Poly2的话,那么权值 wESPN,Adidas就会是一个非常小的负数,而对于FM来说,这个组合的权值由wESPN·wAdidas的内积决定,而这两个向量同时也会用在其他的特征组合中,所以可以得到更准确的预测。
l (NBC, Gucci)这个组合在数据集中是没有的,在Poly2中,对于的预测为0,但是在FM中,对于的特征向量可以通过其他的组合学到。
领域因子分解机(FFM)
Clicked | Publisher (P) | Advertiser (A) | Gender (G) |
Yes | ESPN | Nike | Male |
为了理解FFM,我们需要理解领域的含义,领域是指包含系列特征的比较大范围的种类,比如上面的P(广告发布渠道商,各种网站),A(广告内容上,Nike等),G(性别)。相比于FM,FFM有几个变化:
l 在FM里面,每个潜特征对应了1个向量,学习相互关系的时候(ESPN,Nike)和(ESPN,Male)用到的都是同一个wESPN的向量。
l 然而,由于Nike和Male是属于不同的领域,(ESPN,Nike)的组合效果和(ESPN,Male)的组合效果可能是不一样的,FM不能捕捉这种问题,因为用的都是同一个特征向量。
l 在FFM中,每个特征有好几个潜特征向量组成,比如我们考虑(ESPN,Nike)的组合时,ESPN的向量可以用wESPN,A表示,意思是在(ESPN,Nike)这个组合中使用的向量。同样,如果考虑(ESPN,Male)的组合,我们使用wESPN,G的向量。

FFMs在点击率预测的比赛中获得了第一,已经证明了他的有效性,还获得了 RecSys Challenge 2015的第三,数据集可以在Kaggle上拿到。
使用xLearn的Python实现
几个常用的Python包如下:
Package Name | Description | Package Name |
LibFM | Earliest library by the author himself for FMs | LibFM |
LibFFM | Library exclusively FFMs | LibFFM |
xLearn | Scalable ML package for both FM & FFMs | xLearn |
tffm | Tensorflow implementation of arbitrary order FMs | tffm |
使用FM的时候,需要将数据转换为libffm的格式,这种格式的训练和测试文件是这样子的:
<label> <feature1>:<value1> <feature2>:<value2> …
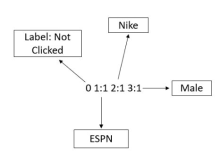
在一个类别字段里面,特征是唯一的,而且赋值为1。
l 对于分类任务,Label是类别号
l 对于回归任务,Label是任意的实数
l 测试文件中的Label只用来计算准确率和loss,如果没有的话,随便写个数字就可以。
FFM也是类似的,只是多了一个领域的字段
<label> <field1>:<feature1>:<value1> <field2>:<feature2>:<value2> …..
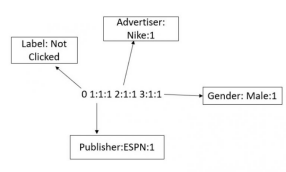
数值特征的注意事项
数值特征需要先进行离散化(先分段,再编码)然后再转换成libffm的格式。或者还可以添加一个dummy的字段,比如45.3可以转换成1:1:45.3。
xLearn
xLearn是最近提出的一个FM和FFM的实现,可以用在多种数据集上,比libFM和libFFM要快的多,而且测试和调试的功能也更好。
我们下面使用一个小数据集来演示一下如何使用xLearn。
我们先需要把数据转换成libffm的格式,代码如下:
1. # Based on Kaggle kernel by Scirpus
2. def convert_to_ffm(df,type,numerics,categories,features):
3. currentcode = len(numerics)
4. catdict = {}
5. catcodes = {}
6. # Flagging categorical and numerical fields
7. for x in numerics:
8. catdict[x] = 0
9. for x in categories:
10. catdict[x] = 1
11.
12. nrows = df.shape[0]
13. ncolumns = len(features)
14. with open(str(type) + "_ffm.txt", "w") as text_file:
15.
16. # Looping over rows to convert each row to libffm format
17. for n, r in enumerate(range(nrows)):
18. datastring = ""
19. datarow = df.iloc[r].to_dict()
20. datastring += str(int(datarow['Label']))
21. # For numerical fields, we are creating a dummy field here
22. for i, x in enumerate(catdict.keys()):
23. if(catdict[x]==0):
24. datastring = datastring + " "+str(i)+":"+ str(i)+":"+ str(datarow[x])
25. else:
26. # For a new field appearing in a training example
27. if(x not in catcodes):
28. catcodes[x] = {}
29. currentcode +=1
30. catcodes[x][datarow[x]] = currentcode #encoding the feature
31. # For already encoded fields
32. elif(datarow[x] not in catcodes[x]):
33. currentcode +=1
34. catcodes[x][datarow[x]] = currentcode #encoding the feature
35. code = catcodes[x][datarow[x]]
36. datastring = datastring + " "+str(i)+":"+ str(int(code))+":1"
37.
38. datastring += '\n'
39. text_file.write(datastring)
xLearn可以处理csv文件和ffm格式的数据,我们将数据转换成ffm格式之后,就可以进行训练了。类似于其他的机器学习算法,我们把数据集划分成训练集和验证集。训练的脚本如下:
1. import xlearn as xl
2.
3. ffm_model = xl.create_ffm()
4. ffm_model.setTrain("criteo.tr.r100.gbdt0.ffm")
5. ffm_model.setValidate("criteo.va.r100.gbdt0.ffm")
6.
7. param = {'task':'binary', # ‘binary’ for classification, ‘reg’ for Regression
8. 'k':2, # Size of latent factor
9. 'lr':0.1, # Learning rate for GD
10. 'lambda':0.0002, # L2 Regularization Parameter
11. 'Metric':'auc', # Metric for monitoring validation set performance
12. 'epoch':25 # Maximum number of Epochs
13. }
14.
15. ffm_model.fit(param, "model.out")
训练的log:

还可以使用交叉验证
ffm_model.cv(param)
在测试集上进行测试:
1. # Convert output to 0/1
2. ffm_model.setTest("criteo.va.r100.gbdt0.ffm")
3. ffm_model.setSigmoid()
4. ffm_model.predict("model.out", "output.txt")
结束语
在本文中,我们演示了如何使用因子分解的方式来进行分类和回归。xLearn的更多信息请看这个链接link,这里会持续的更新。
原文链接:
https://www.analyticsvidhya.com/blog/2018/01/factorization-machines/
本文为AI公园编译,转载请联系本公众号获得授权
这篇关于入门指南-因子分解机及其在大数据集上的应用(含Python代码)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






