本文主要是介绍【读论文】Trans系列知识表示学习方法梳理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近要做一个知识库问答系统,再加上对表示推理有了一点不知道对错的想法,于是翻出来知识表示学习经典的Trans系列,把论文里描述的模型和清华THUNLP提供的Tensorflow版程序一起看。
一点关于知识表示学习的背景知识
知识图谱通常是用一个三元组(前件h,关系r,后件t)来表示一条知识,比如:(中国科学院大学,地点,北京),要使用向量表示的话,可以使用one-hot向量(实际使用中通常是mulit-hot向量)来表示。但是问题也来了,one-hot向量维数太高,而且无法表示相近的实体或关系之间的相似程度。所以类比词向量的表示方法,也想使用分布式表示(distributed representation)来表示知识图谱中的实体和关系,通过学习获得它们的低维稠密表示。
TransE
论文题目:Translating Embeddings for Modeling Multi-relational Data(2013)
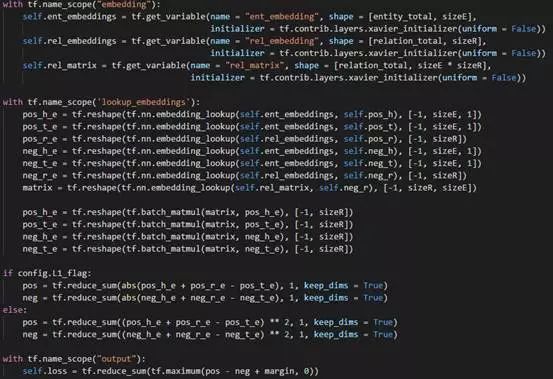
这是Trans系列的第一篇文章,模型的基本想法是前件的向量表示h与关系的向量表示r之和与后件的向量表示t越接近越好,即h+r≈t。这里的“接近”可以使用L1或L2范数进行衡量。
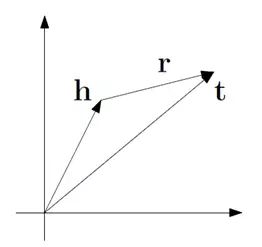
要优化的目标函数使用带negative sampling的max margin损失函数,即L(y,y’)=max(0,margin−y+y’),其中y表示正样本的得分,y’表示负样本的得分。最小化这个损失函数可以使正样本的得分越来越高而负样本的得分越来越低,但是两个得分差距大到一定程度(margin)就足够了,再大的话得到的loss也只是0。在这里因为正负样本得分用的是距离,所以要加负号,即最终的损失函数为
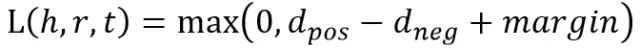
其中
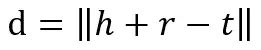
为L1或者L2范数。论文中获得负样本并不是随机选取其他的三元组,其中还有一个trick,将正样本三元组中的前件或后件替换为一个随机的实体已获取负样本。
来看看对应的代码。
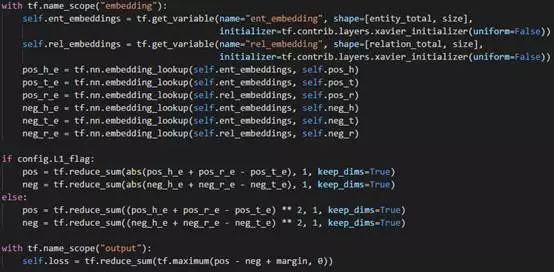
使用embedding_lookup从大矩阵里获得对应的向量h、r、t,计算h与r之和与t的距离并代入损失函数,也很简单明了。
但是模型的简单也就带来了问题,它只适合处理一对一的关系,不适合一对多/多对一的关系。举个例子,有两个三元组(中国科学院大学,地点,北京)和(颐和园,地点,北京),使用TransE进行表示的话会得到中国科学院大学的表示向量和颐和园的表示向量很接近,甚至完全相同。但是它们的亲密度实际上可能没有这么大。
TransH
论文题目:Knowledge Graph Embedding by Translating on Hyperplanes(2014)
TransH模型的目的就在于处理一对多/多对一的关系问题,而又不过分增加模型的复杂度和训练难度。模型的基本思想是针对每一个关系r,将前件h和后件t的向量表示投影到一个由向量wr确定的超平面得到向量h⊥和t⊥,在这个超平面上存在一个关系的表示向量r,与TransE一样通过训练使得h⊥+r≈t⊥,因此每一个关系实际上是由向量wr和向量r共同表示的。
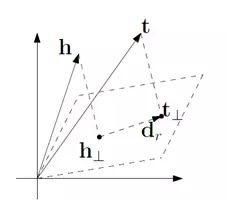
其中向量在超平面上的投影是这样计算的:
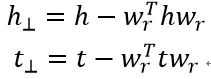
移项后
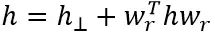
可以看到实际上是将向量h在向量wr方向(垂直超平面)和垂直于wr方向(超平面上)进行分解,由于论文中限制向量wr长度为1,因此实际上上式后面那一项其实是h在wr方向上的投影。
目标函数和训练方法和TransE模型一模一样,不多赘述。
由于对前件和后件的表示向量进行了分解,因此在使用h和r计算t的时候相当于只使用了向量h的一个分量,因此避免了TransE模型在处理一对多/多对一问题时将两个实体收敛到过于接近的情况。
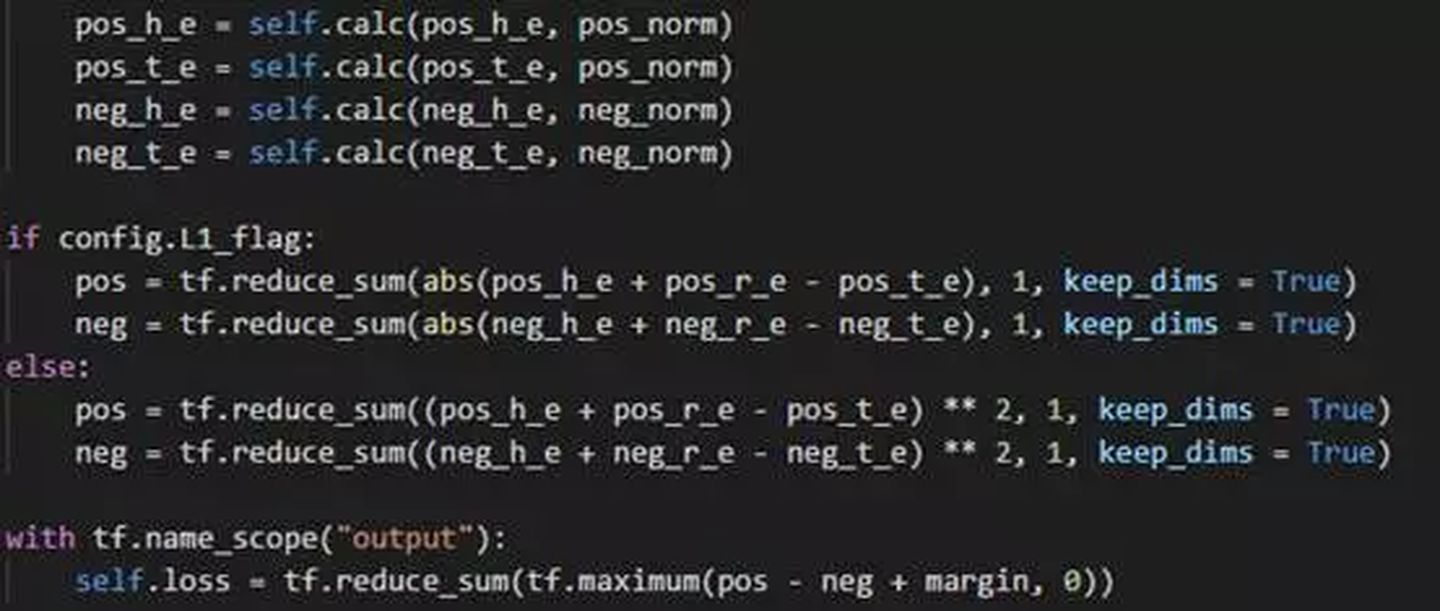

代码与TransE基本相同,多了一步计算投影向量的过程,并且在计算投影之前将向量wr归一化至单位长度。
TransR
论文题目:Learning Entity and Relation Embeddings forKnowledge Graph Completion(2015)
TransE和TransH模型都假设实体和关系是在同一个语义空间的向量,这样相似的实体会在空间中相近的位置,然而每一个实体都可以有很多方面,而不同的关系关注的是实体不同的方面。因此,TransR模型对不同的关系建立各自的关系空间,在计算时先将实体映射到关系空间进行计算。因为是在关系空间做向量叠加,所以这个模型叫做TransR。
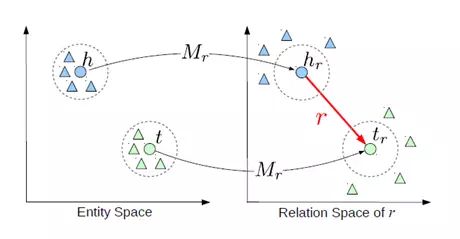
对于每个关系,有一个变换矩阵Mr和一个在它自己的关系空间的表示向量r。通过变换矩阵将前件和后件的表示向量映射到关系空间
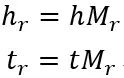
再在关系空间通过训练使得hr+r≈tr。目标函数和训练方法和TransE模型一模一样,不多赘述。
TransR还有一个变体叫做CTransR,其中的C是Cluster聚类。CTransR考虑的问题是对一个关系只用一个表示无法体现这一种关系的多义性,比如关系(location location contains)其实包含country-city、country-university、continent-country等多种含义。因此对于某一种关系的全部实体对(h,t),用h减去t的向量作为它的表示(h和t通过TransE模型得到),对其进行聚类,对于每一类的子关系都学习一个变换矩阵Mr和一个表示向量r,接下来就和TransR模型一样了。
由于在构造负样本时替换的是前件或者后件,而关系并没有替换,因此在代码中对于正负样本只获取了一个变换矩阵。除了在计算距离之前先乘上矩阵进行变换,其他的和TransE模型基本一样。
TransD
论文题目:Knowledge Graph Embedding via Dynamic Mapping Matrix(2015)
TransR同样有它的问题,首先对于一种关系,它的前件和后件使用同样的变换矩阵映射到关系空间,而前件和后件往往是完全不同类的实体,比如(刘康,工作单位,中科院自动化所),其中刘康老师和自动化所就是不同范畴的实体,也应该使用不同的方法进行映射。其次,这种映射是与实体和关系都相关的过程,然而映射矩阵却只由关系确定。最后,TransR模型运算量大且参数较前两种模型多得多。(画外音:以上来自TransD论文原文,好犀利的三条问题)
TransD模型对每个实体或关系使用两个向量进行表示,一个向量表示语义,另一个(用下表p表示)用来构建映射矩阵。映射矩阵通过以下式子构建

这样映射矩阵就由实体和关系共同决定了,其中I为单位阵,即通过向量相乘生成的矩阵对单位阵(代表不做变换)进行调整。后面的映射和训练过程和TransR相同。
这样的话,TransE模型就变成了TransD模型的一个特例,只要实体表示的维度与关系表示的维度相同且所有用于构建映射矩阵的向量均为0。此外,上面构建映射矩阵和进行空间变换的过程还可以用向量相乘代替,从而避免了耗时的矩阵乘法,即

补0是因为这里假设关系空间维度比实体空间维度高。
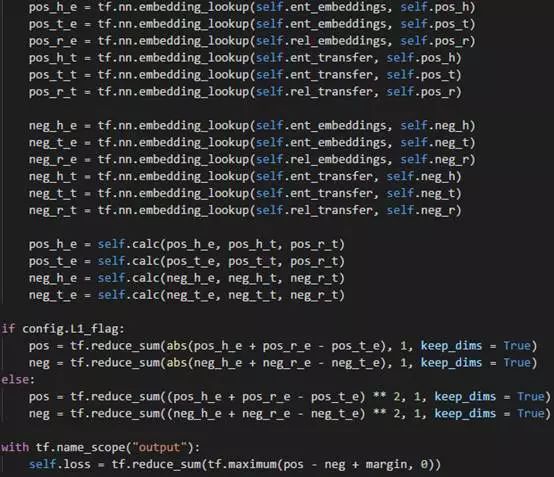

代码也和前面的结构一样,这里可以看到每个实体或关系是由两个向量表示的,并使用了不需要进行矩阵运算的方法得到实体在关系空间的映射。不过看起来这个代码并没有实现实体空间和关系空间维数不同的情况。
结语
每个模型的论文都有它自己的tricks,在这里没有详细叙述。
最后有一点感觉,这些模型(包括之后AAAI2016还有一个TransSparse,使用不同程度的稀疏矩阵进行从实体空间到关系空间的变换)都是基于最初TransE模型的生长,即使用前件和关系向量之和来预测后件向量。向量之和从某种程度是表示的是信息的叠加,但是实体和关系或许不仅仅是信息的叠加而已。
这篇关于【读论文】Trans系列知识表示学习方法梳理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




