树：线索化二叉树

2024-06-21 02:38
文章标签 二叉树 线索

本文主要是介绍树：线索化二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1，线索化二叉树基本介绍

  • 线索化二叉树是对普通二叉树的扩展，对于普通二叉树而言，一个节点会包含一个数据域以及指向左右子节点的位置索引；但是对于叶子节点来讲，左右子节点的位置索引并没有被利用到，线索二叉树充分利用该部分节点，普通二叉树如下：
    在这里插入图片描述
  • 在n个节点的二叉树中总共含有n - 1（类似5指向2表示一个位置指向）个位置指向，即2n（每一个节点有左右两个指针域）个指针域，这样对于一个二叉树来讲，共有2n - (n - 1) = n + 1个空指针域。利用二叉树的空指针域，根据前/中/后序不同遍历方式存储前驱节点（左子节点）和后继节点（右子节点），这种附加的指针称为线索，二叉树转线索化二叉树，后续会分别具体分析：
  • 根据线索性质的不同，线索二叉树可以分为前序线索二叉树，中序线索二叉树，后续线索二叉树；分别对应前序遍历方式，中序遍历方式，后续遍历方式，部分方式的线索二叉树必须对应不同的遍历方式，不然会遍历失败，甚至栈溢出
  • 二叉树转换为线索化二叉树后，leftNode指向的可能是左子树，也可能是前驱节点；同样，rightNode指向的可能是右子树，也可能是后继节点；具体区分，会在Node节点对象中分别维护leftFlag和rightFlag属性，对应不同的标志位标识是线索节点还是真实节点

2，二叉树 — 线索化二叉树转换规则

  • 线索化二叉树是在原二叉树的基础上，将每一个节点抽象为存在上下指针的节点
  • 在将二叉树转换为线索化二叉树时，
  • 如果节点的左右节点存在，则该节点不变，
  • 如果节点的左侧节点为空, 则将左侧节点填充为前驱节点；中序方式的遍历方式为：左中右，可以通过不同位置对应前驱节点
  • 如果节点的右侧节点为空，则将右侧节点填充为后继节点，选择同上
  • 另外，在Node节点中除过leftNode，rightNode左右节点数据外，另外维护leftFlag，rightFlag两个标志位，说明当前左/右侧数据指示的是树数据，还是后继节点数据
  • 对于前序/中序/后序方式生成的线索化二叉树，必须对应的使用前序/中序/后序方式进行遍历
  • 遍历结果的第一个元素和最后一个元素，分别没有前驱节点和后继节点，所以在线索化二叉树中对应的指向Node为空，但Flag指示为前驱/后继节点

3，中序线索化二叉树

3.1，转换规则

  • 中序输出规则为先输出左侧节点，再输出当前节点，最后输出右侧节点
  • 如果左侧节点为空，递归左侧进行处理
  • 处理当前节点
    • 如果左侧节点为空，填充为前驱节点，即 preNode，此时如果该节点是第一个需要遍历的节点，则preNode为空，单leftFlag会被修改为前驱节点
    • 如果右侧节点为空，填充为后继节点，同样，如果该节点是最后一个节点，则值为空，标志位为后继节点
    • 因为当前节点拿不到下一个树节点，所以填充右侧后继节点需要遍历到下一个节点后进行处理，等到遍历到下一个节点时, 此时当前节点为 preNode
    • 当前节点(preNode)的后继节点即下一个节点，也就是当前遍历到的节点，此时设置后继节点, 即把当前遍历到的节点设置为preNode的右侧节点
  • 如果右侧节点不为空，递归右侧进行处理

3.2，示意图

在这里插入图片描述

  • 上图表示二叉树转换为线索化二叉树后的节点关系，即前驱后继节点关联关系
  • 其中蓝色数字表示数节点，红色数组表示前驱/后继节点
  • 实线表示左右节点的连线关系，虚线表示节点的前驱后继关联关系
  • 9节点旁边的8颜色标错了，应该是红色

3.3，遍历规则

  • 首先一直向左循环拿到leftFlag标志为前驱节点的节点，表示最左侧节点，也就是中序遍历需要遍历到的第一个节点
  • 中序遍历方式的节点打印顺序为：左中右
  • 此时先打印该节点，表示遍历到的第一个节点
  • 打印完成后，循环向右找后继节点的右侧节点并顺序打印
  • 直接循环到有效树节点，则以该节点为顶层节点，继续第一步处理

3.4，代码示例

package com.self.datastructure.tree.binarytree;import lombok.Data;
import lombok.ToString;/*** 线索化二叉树** @author pj_zhang* @create 2020-03-23 22:12**/
public class ClueBinaryTree {public static void main(String[] args) {MyBinaryTree binaryTree = new MyBinaryTree();binaryTree.addNode(5);binaryTree.addNode(2);binaryTree.addNode(1);binaryTree.addNode(4);binaryTree.addNode(3);binaryTree.addNode(8);binaryTree.addNode(6);binaryTree.addNode(9);binaryTree.addNode(7);// 中序生成线索化二叉树System.out.println("中序生成线索化二叉树...");binaryTree.middleClueBinaryTree();System.out.println("\r\n中序遍历线索化二叉树...");binaryTree.middleShowDetails();binaryTree.postShowDetails();}static class MyBinaryTree {private Node node;/*** 指向前一个节点, 用于下一个节点时的上一个节点操作* 上一个节点的右节点为空时, 需要指向下一个节点,* 此时设置该节点的右节点信息, 需要等操作到下一个节点, 用preNode节点作为该节点设置*/private Node preNode;// 中序生成线索二叉树public void middleClueBinaryTree() {doMiddleClueBinaryTree(node);}public void doMiddleClueBinaryTree(Node node) {if (null == node) {return;}// 左侧递归处理if (node.getLeftFlag() == 0) {doMiddleClueBinaryTree(node.getLeftNode());}// 直接输出当前节点System.out.print(node.getData() + "  ");// 填充左侧节点// 左侧节点为空, 填充为前驱节点if (null == node.getLeftNode()) {// 中序: 第一个输出的节点的左侧节点必定为空node.setLeftNode(preNode);node.setLeftFlag(1);}// 填充右侧节点// 右侧节点为空, 填充为后继节点// 填充下一个节点是, 需要遍历到下一个节点进行填充// 则此时当前节点表示为上一个节点, 即preNodeif (null != preNode && null == preNode.getRightNode()) {preNode.setRightNode(node);preNode.setRightFlag(1);}// 将当前节点设置为上一个节点preNode = node;// 右侧递归处理if (node.getRightFlag() == 0) {doMiddleClueBinaryTree(node.getRightNode());}}// 中序遍历线索二叉树public void middleShowDetails() {doMiddleShowDetails(node);}public void doMiddleShowDetails(Node node) {for (;null != node;) {// 首先循环找到leftFlag为1的节点// 表示左侧的叶子节点for (;node.getLeftFlag() == 0;) {node = node.getLeftNode();}// 先打印该节点System.out.print(node.getData() + "  ");// 右侧节点状态为1, 说明是下一个节点, 直接打印for (;node.getRightFlag() == 1;) {node = node.getRightNode();System.out.print(node.getData() + "  ");}// 走到此处说明找到有效的右侧节点, 替换掉该节点node = node.getRightNode();}}}@Data@ToStringstatic class Node {private Integer data;private Node leftNode;private Node rightNode;/*** 左侧节点标志位,* 0表示存在左侧节点, 1表示左侧节点为前继节点*/private int leftFlag;/*** 右侧节点标志位* 0表示存在右侧节点, 1表示右侧节点为后续节点*/private int rightFlag;public Node() {}public Node(Integer data) {this(data, null, null);}public Node(Integer data, Node leftNode, Node rightNode) {this.data = data;this.leftNode = leftNode;this.rightNode = rightNode;}}}

4，前序线索化二叉树

4.1，转换规则

  • 前序相对于中序来讲相对比较简单
  • 前序输出规则为：先输出当前节点，再输出左侧节点，最后输出右侧节点
  • 处理当前节点
    • 填充规则与中序完全一致
    • 左侧节点为空，填充preNode节点为前驱节点
    • 右侧节点为空，填充下一个遍历到的节点为后继节点
  • 再递归处理左侧节点，此时注意左侧节点如果为前驱节点则不处理
  • 最后递归处理右侧节点，右侧节点为后继节点则不处理

4.2，示意图

在这里插入图片描述

4.3，便利规则

  • 前序遍历相对于中序遍历稍微简单
  • 前序遍历首先从顶层节点向左遍历，如果左侧节点为有效树节点，则输出后继续向左遍历
  • 最终遍历到一个节点的左侧节点为前驱节点，则获取该节点的右侧节点继续进行遍历
  • 此时右侧节点可能为后继节点，也可能为有效的树节点，但在前序中区分的意义不大，可以直接遍历打印，直到遍历到最后一个节点，其右侧几点即后继节点为null

4.4，代码示例

package com.self.datastructure.tree.binarytree;import lombok.Data;
import lombok.ToString;/*** 线索化二叉树* * 线索化二叉树是在原二叉树的基础上, 将每一个节点抽象为存在上下指针的节点* * 在将二叉树转换为线索化二叉树时* * 如果节点的左右节点存在, 则该节点不变* * 如果节点的左侧节点为空, 则将左侧节点填充为上一个节点,*   上一个节点选择根据前序, 中序, 后序不同变化* * 如果节点的右侧节点为空, 则将右侧节点填充为下一个节点, 选择同上* * 另外, 在Node节点中除过leftNode, rightNode左右节点数据外,*   另外维护leftFlag, rightFlag两个标志位, 说明当前左/右侧数据指示的是树数据, 还是下一个节点数据* * 对于前序/中序/后序方式生成的线索化二叉树, 必须对应的使用前序/中序/后序方式进行遍历* * 遍历结果的第一个元素和最后一个元素, 分别没有前一个元素和后一个元素,*   所以在线索化二叉树中对应的指向Node为空, 但Flag指示为上/下一个节点** @author pj_zhang* @create 2020-03-23 22:12**/
public class ClueBinaryTree {public static void main(String[] args) {MyBinaryTree binaryTree = new MyBinaryTree();binaryTree.addNode(5);binaryTree.addNode(2);binaryTree.addNode(1);binaryTree.addNode(4);binaryTree.addNode(3);binaryTree.addNode(8);binaryTree.addNode(6);binaryTree.addNode(9);binaryTree.addNode(7);// 前序生成线索二叉树System.out.println("\r\n前序生成线索化二叉树");binaryTree.preClueBinaryTree();System.out.println("\r\n前序遍历线索化二叉树");binaryTree.preShowDetails();}static class MyBinaryTree {private Node node;/*** 指向前一个节点, 用于下一个节点时的上一个节点操作* 上一个节点的右节点为空时, 需要指向下一个节点,* 此时设置该节点的右节点信息, 需要等操作到下一个节点, 用preNode节点作为该节点设置*/private Node preNode;// 前序生成线索化二叉树// 规则参考中序public void preClueBinaryTree() {doPreClueBinaryTree(node);}public void doPreClueBinaryTree(Node node) {if (null == node) {return;}// 先处理当前节点// 先输出当前节点System.out.print(node.getData() + "  ");// 左侧节点为空, 填充为上一个节点if (null == node.getLeftNode()) {node.setLeftNode(preNode);node.setLeftFlag(1);}// 右侧节点为空, 填充为下一个节点if (null != preNode && null == preNode.getRightNode()) {preNode.setRightNode(node);preNode.setRightFlag(1);}preNode = node;// 再处理左侧节点// 注意一定要加leftFlag判断, 不然容易死递归if (node.getLeftFlag() == 0) {doPreClueBinaryTree(node.getLeftNode());}// 最后处理右侧节点if (node.getRightFlag() == 0) {doPreClueBinaryTree(node.getRightNode());}}/*** 前序遍历*/public void preShowDetails() {doPreShowDetails(node);}public void doPreShowDetails(Node node) {for (;null != node;) {// 左侧节点为有效节点, 直接输出for (;0 == node.getLeftFlag();) {System.out.print(node.getData() + "  ");node = node.getLeftNode();}// 输出最后一个左侧有效节点System.out.print(node.getData() + "  ");// 该节点右侧节点指向下一个节点node = node.getRightNode();}}// 添加二叉树节点public void addNode(Integer data) {if (null == node) {node = new Node(data);} else {addNode(data, node);}}private void addNode(Integer data, Node node) {if (null == node) {throw new RuntimeException("Node 节点为空");}if (data > node.getData()) {Node rightNode = node.getRightNode();if (null == rightNode) {node.setRightNode(new Node(data));} else {addNode(data, node.getRightNode());}} else if (data < node.getData()) {Node leftNode = node.getLeftNode();if (null == leftNode) {node.setLeftNode(new Node(data));} else {addNode(data, node.getLeftNode());}} else {System.out.println("数据节点已经存在");}}}@Data@ToStringstatic class Node {private Integer data;private Node leftNode;private Node rightNode;/*** 左侧节点标志位,* 0表示存在左侧节点, 1表示左侧节点为前继节点*/private int leftFlag;/*** 右侧节点标志位* 0表示存在右侧节点, 1表示右侧节点为后续节点*/private int rightFlag;public Node() {}public Node(Integer data) {this(data, null, null);}public Node(Integer data, Node leftNode, Node rightNode) {this.data = data;this.leftNode = leftNode;this.rightNode = rightNode;}}}

5，后序线索化二叉树

5.1，转换规则

  • 后续输出的顺序为：先输出左侧节点，再输出右侧节点，最后输出当前节点
  • 所以在后续转换时，先递归处理左侧节点
  • 再递归处理右侧节点
  • 最后处理当前节点，当前节点的前驱和后继节点填充与之前完成一致
  • 重点：后续输出顺序为左右中，所以对于一个完整子树来说，左右侧输出完成后，右侧的后继节点为它的父节点，即中间节点；此时中间节点如果为左侧节点，输出后需要再次输出其对应的右侧节点，也就是parentNode.rightNode，以之前前序中序的转换和遍历法则肯定不足以满足，需要在Node实体类中添加parentNode属性
  • 添加完parentNode属性后，在二叉树转换线索化二叉树时，可直接对该属性进行维护

5.2，示意图

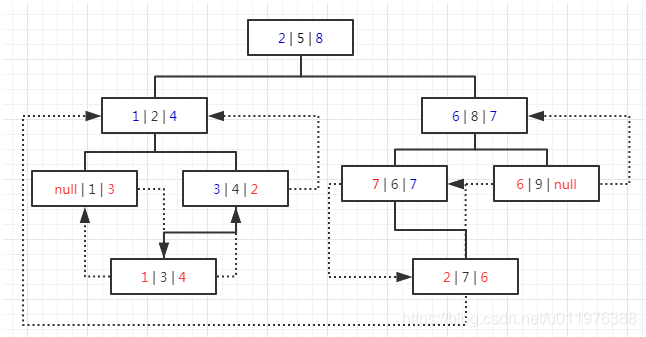
在这里插入图片描述

5.3，遍历规则

  • 后续遍历与前序和中序有所不同，并且相对复杂，后续遍历注意添加了一个新属性：parentNode
  • 因为后续遍历的打印顺序为：左右中，所以首先还是获取最左侧节点，即leftFlag为0的最左侧节点，
  • 首先判断右侧节点是否为后继节点，如果右侧节点为后继节点，则打印该节点，并循环继续判断下一个右侧节点，直接非后继节点为止
  • 获取到非后继节点后，判断当前节点的右侧节点与上一个处理节点是否一致，或者在当前节点的右侧节点为后继节点时，当前节点的左侧节点与上一个处理节点是否一致
  • 如果上一步能匹配到，说明以当前节点为顶层节点的子树已经遍历完成， 继续以该节点的父节点进行上一步判断，并以此类推
  • 如果上一步没有匹配到，则说明上一个处理节点为当前节点的左侧节点，需要继续遍历左树进行处理，则对node重新赋值左树处理

5.4，代码示例

package com.self.datastructure.tree.binarytree;import lombok.Data;
import lombok.ToString;/*** 线索化二叉树* * 线索化二叉树是在原二叉树的基础上, 将每一个节点抽象为存在上下指针的节点* * 在将二叉树转换为线索化二叉树时* * 如果节点的左右节点存在, 则该节点不变* * 如果节点的左侧节点为空, 则将左侧节点填充为上一个节点,*   上一个节点选择根据前序, 中序, 后序不同变化* * 如果节点的右侧节点为空, 则将右侧节点填充为下一个节点, 选择同上* * 另外, 在Node节点中除过leftNode, rightNode左右节点数据外,*   另外维护leftFlag, rightFlag两个标志位, 说明当前左/右侧数据指示的是树数据, 还是下一个节点数据* * 对于前序/中序/后序方式生成的线索化二叉树, 必须对应的使用前序/中序/后序方式进行遍历* * 遍历结果的第一个元素和最后一个元素, 分别没有前一个元素和后一个元素,*   所以在线索化二叉树中对应的指向Node为空, 但Flag指示为上/下一个节点** @author pj_zhang* @create 2020-03-23 22:12**/
public class ClueBinaryTree {public static void main(String[] args) {MyBinaryTree binaryTree = new MyBinaryTree();binaryTree.addNode(5);binaryTree.addNode(2);binaryTree.addNode(1);binaryTree.addNode(4);binaryTree.addNode(3);binaryTree.addNode(8);binaryTree.addNode(6);binaryTree.addNode(9);binaryTree.addNode(7);// 后续生成线索二叉树System.out.println("\r\n后续生成线索化二叉树");binaryTree.postClueBinaryTree();System.out.println("\r\n后续遍历线索化二叉树");binaryTree.postShowDetails();}static class MyBinaryTree {private Node node;/*** 指向前一个节点, 用于下一个节点时的上一个节点操作* 上一个节点的右节点为空时, 需要指向下一个节点,* 此时设置该节点的右节点信息, 需要等操作到下一个节点, 用preNode节点作为该节点设置*/private Node preNode;/*** 后续生成线索化二叉树*/public void postClueBinaryTree() {doPostClueBinaryTree(node, null);}public void doPostClueBinaryTree(Node node, Node parentNode) {if (null == node) {return;}// 先处理左侧节点doPostClueBinaryTree(node.getLeftNode(), node);// 在处理右侧节点doPostClueBinaryTree(node.getRightNode(), node);// 最后处理当前节点// 先输出当前节点System.out.print(node.getData() + "  ");// 左侧节点为空, 填充为上一个节点if (null == node.getLeftNode()) {node.setLeftNode(preNode);node.setLeftFlag(1);}// 右侧节点为空, 填充为下一个节点if (null != preNode && null == preNode.getRightNode()) {preNode.setRightNode(node);preNode.setRightFlag(1);}// 后序注意填充父节点node.setParentNode(parentNode);preNode = node;}/*** 后续遍历线索化二叉树*/public void postShowDetails() {doPostShowDetails(node);}public void doPostShowDetails(Node node) {Node preNode = null;for (;null != node;) {// 获取到最左侧数据for (;0 == node.getLeftFlag();) {node = node.getLeftNode();}// 首先判断右侧节点是否是后继节点// 右侧节点为后继节点, 直接打印该节点for (;1 == node.getRightFlag();) {System.out.print(node.getData() + "  ");// 设置上一个节点为当前节点preNode = node;// 并将遍历节点指向后继节点node = node.getRightNode();}// 能走到这一步说明右侧节点不是后继节点// 并且上一个操作的节点一定是当前节点的子节点(无论是单左子节点还是单右子节点, 或者左右子节点都有, 都会最终指向该节点)// 此时对上一个操作节点进行判断:// 如果上一个节点是当前节点的右子节点, 说明以该节点为顶点的子树已经遍历完成, 打印该节点后, 继续回退到父节点进行处理// 或者说如果上一个节点是当前节点的左子节点, 但当前节点不存在右子节点, 依旧回退到父节点进行继续处理// 如果上一个节点是当前节点的左子节点且存在右子节点, 则直接继续处理右子树for (;preNode == node.getRightNode() || (1 == node.getRightFlag() && preNode == node.getLeftNode());) {System.out.print(node.getData() + "  ");// 如果当前节点是根节点, 直接退出if (this.node == node) {return;}// 当前节点不是根节点, 继续往下走preNode = node;node = node.getParentNode();}// 上一个节点不是右侧节点// 则必定是左侧节点,node = node.getRightNode();}}// 添加二叉树节点public void addNode(Integer data) {if (null == node) {node = new Node(data);} else {addNode(data, node);}}private void addNode(Integer data, Node node) {if (null == node) {throw new RuntimeException("Node 节点为空");}if (data > node.getData()) {Node rightNode = node.getRightNode();if (null == rightNode) {node.setRightNode(new Node(data));} else {addNode(data, node.getRightNode());}} else if (data < node.getData()) {Node leftNode = node.getLeftNode();if (null == leftNode) {node.setLeftNode(new Node(data));} else {addNode(data, node.getLeftNode());}} else {System.out.println("数据节点已经存在");}}}@Data@ToStringstatic class Node {private Integer data;private Node leftNode;private Node rightNode;/*** 后续序列化使用*/private Node parentNode;/*** 左侧节点标志位,* 0表示存在左侧节点, 1表示左侧节点为前继节点*/private int leftFlag;/*** 右侧节点标志位* 0表示存在右侧节点, 1表示右侧节点为后续节点*/private int rightFlag;public Node() {}public Node(Integer data) {this(data, null, null);}public Node(Integer data, Node leftNode, Node rightNode) {this.data = data;this.leftNode = leftNode;this.rightNode = rightNode;}}}

这篇关于树：线索化二叉树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1079977。

相关文章

leetcode105 从前序与中序遍历序列构造二叉树

leetcode105 从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。 注意: 你可以假设树中没有重复的元素。 例如，给出 前序遍历 preorder = [3,9,20,15,7]中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树： 3/ \9 20/ \15 7   class Solution {public TreeNode buildTree(int[] pr
阅读更多...
PHP实现二叉树遍历(非递归方式，栈模拟实现)

PHP实现二叉树遍历(非递归方式，栈模拟实现)

二叉树定义是这样的：一棵非空的二叉树由根结点及左、右子树这三个基本部分组成，根据节点的访问位置不同有三种遍历方式： ① NLR：前序遍历(PreorderTraversal亦称(先序遍历)) ——访问结点的操作发生在遍历其左右子树之前。 ② LNR：中序遍历(InorderTraversal) ——访问结点的操作发生在遍历其左右子树之中(间)。 ③ LRN：后序遍历(PostorderT
阅读更多...
在二叉树中找到两个节点的最近公共祖先（基于Java）

在二叉树中找到两个节点的最近公共祖先（基于Java）

如题  题解 public int lowestCommonAncestor(TreeNode root, int o1, int o2) {//记录遍历到的每个节点的父节点。Map<Integer, Integer> parent = new HashMap<>();Queue<TreeNode> queue = new LinkedList<>();parent.put(roo
阅读更多...
数据结构--二叉树（C语言实现，超详细！！！）

数据结构--二叉树（C语言实现，超详细！！！）

文章目录 二叉树的概念代码实现二叉树的定义创建一棵树并初始化组装二叉树前序遍历中序遍历后序遍历计算树的结点个数求二叉树第K层的结点个数求二叉树高度查找X所在的结点查找指定节点在不在完整代码 二叉树的概念 二叉树（Binary Tree）是数据结构中一种非常重要的树形结构，它的特点是每个节点最多有两个子节点，通常称为左子节点和右子节点。这种结构使得二叉树在数据存储和查找等方面具
阅读更多...
笔试强训,[NOIP2002普及组]过河卒牛客.游游的水果大礼包牛客.买卖股票的最好时机（二)二叉树非递归前序遍历

笔试强训,[NOIP2002普及组]过河卒牛客.游游的水果大礼包牛客.买卖股票的最好时机（二)二叉树非递归前序遍历

目录 [NOIP2002普及组]过河卒 牛客.游游的水果大礼包 牛客.买卖股票的最好时机（二) 二叉树非递归前序遍历 [NOIP2002普及组]过河卒 题里面给的提示很有用，那个马的关系，后面就注意，dp需要作为long的类型。 import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息publ
阅读更多...
222.完全二叉树的节点个数

222.完全二叉树的节点个数

（写给未来遗忘的自己） 题目： 代码： class Solution {public:int countNodes(TreeNode* root) {queue<TreeNode*>node_que;if(root==nullptr) return 0;node_que.push(root);int result;while(!node_que.empty()){int layer_s
阅读更多...
代码随想录 -- 二叉树 -- 平衡二叉树

代码随想录 -- 二叉树 -- 平衡二叉树

110. 平衡二叉树 - 力扣（LeetCode） 思路：仍然是递归调用 1. 定义一个递归函数 count 用来计算二叉树的层数 2. isBalanced 函数：如果传入根节点为空返回真；如果根节点 | 左子树的层数 - 右子树的层数 | 大于1，返回假；最后返回根节点左子树、右子树是否是平衡二叉树。 class Solution(object):def count(self,root
阅读更多...
【数据结构】你真的学会了二叉树了吗，来做一做二叉树的算法题及选择题

【数据结构】你真的学会了二叉树了吗，来做一做二叉树的算法题及选择题

文章目录 1. 二叉树算法题1.1 单值二叉树1.2 相同的树1.3 另一棵树的子树1.4 二叉树的遍历1.5 二叉树的构建及遍历 2. 二叉树选择题3. 结语 1. 二叉树算法题 1.1 单值二叉树 https://leetcode.cn/problems/univalued-binary-tree/description/ 1.2 相同的树 https://leet
阅读更多...
二叉树的层次遍历（10道）

二叉树的层次遍历（10道）

（写给未来遗忘的自己） 102.二叉数的层序遍历（从上到下） 题目： 代码： class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> result; queue<TreeNode*> node; if (root == nullptr) {
阅读更多...
求二叉树的深度——（力扣c语言）

求二叉树的深度——（力扣c语言）

题目如下： 给定一个二叉树 root ，返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1： 输入：root = [3,9,20,null,null,15,7]输出：3 示例 2： 输入：root = [1,null,2]输出：2 题目解析： 上题就是要利用递归对目标进行访问找到叶子节点之后记录并返回到根节点之后对左右两个
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2