SpingBoot快速入门下

本文主要是介绍SpingBoot快速入门下，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

响应HttpServietResponse

介绍

• 将@ResponseBody 加到Controller方法/类上

• 作用：将方法返回值直接响应，如果返回值是 实体对象/集合，将会自动转JSON格式响应

• @RestController = @Controller + @ResponseBody;

一般响应

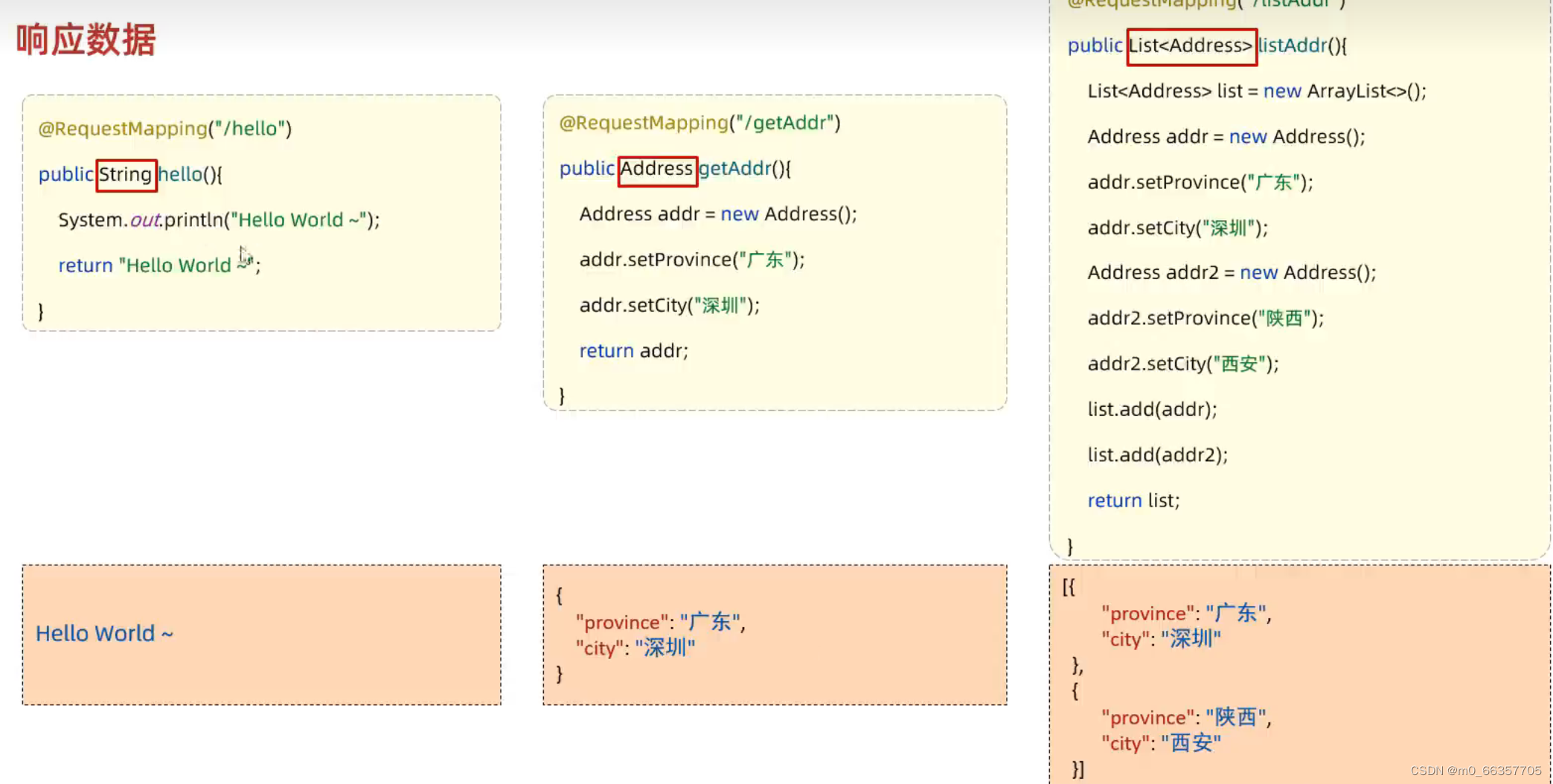
统一响应

• 在实际开发中一般不会用不同的类作为响应，因为不方便管理，一般会有一个类统一响应

• 一般会带状态码，和响应类型

public class Result{//响应状态 如 1代表成功 0失败private Integer status;//提示信息，告诉前端我响应的是响应private String msg;//数据部分private Object data;//所有get/set方法  要确保data的对象的属性也有所有set/get方法//返回的json 格式是根据getXXX(); XXX的名称来命名键名,本且转小写
}

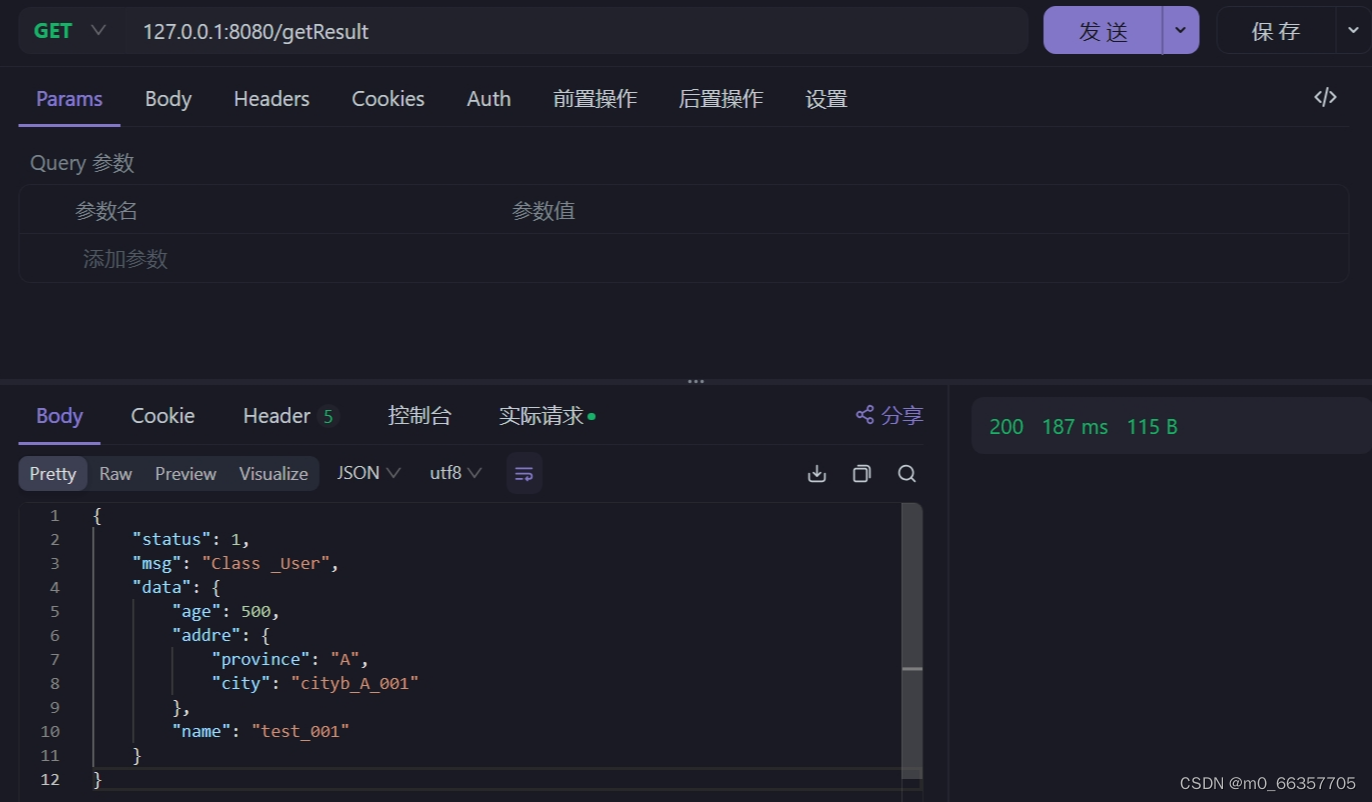
@RestController
public class TestController{ //一般响应@RequestMapping("/getData")public _User getData(){System.out.println("getDataRequest");_User user = new _User();user.test = "test_001";user.age= 500;user.addre = new Address();user.addre.province = "A";user.addre.city = "cityb_A_001";return user;}//统一响应@RequestMapping("/getResult")public Result getResult(){System.out.println("getResult");_User user = new _User();user.test = "test_001";user.age= 500;user.addre = new Address();user.addre.province = "A";user.addre.city = "cityb_A_001";Result res = new Result();res.status = 1;             //表示成功res.msg = "Class _User";     //表示数据是_User 类res.data = user;return res;}
}

总结

@ResponseBody 注解

• 定义: @ResponseBody是Spring MVC框架中的一个注解，它的作用是指示方法的返回值应该直接作为响应体返回给客户端，而不是返回一个视图（View）。

• 使用场景:

  • 当你想要返回JSON、XML等数据格式，而不是跳转到一个页面。

  • 当你正在构建RESTful API，需要直接返回数据而不是视图。

• 工作原理:

  • @ResponseBody注解的方法，其返回值将被Spring MVC的HttpMessageConverter转换成客户端请求的格式（如JSON）。

  • 如果方法返回的是String类型，Spring MVC会将这个字符串直接写入响应体。

• 示例:

  @RequestMapping("/greeting")
  @ResponseBody
  public String greeting() {return "Hello, World!";
  }

  上述代码中，访问

  /greeting

  路径将直接返回字符串"Hello, World!"作为响应体。

统一响应结果

• 目的: 统一的响应格式有助于前后端分离的开发模式，使得前端开发者可以更容易地处理来自后端的数据。

• 组成部分:

  • code: 通常是一个整数，表示请求的处理结果。例如，200表示成功，404表示未找到，500表示服务器错误等。

  • msg: 是一个字符串，提供关于响应的额外信息。在成功时，可能是操作的描述；在失败时，提供错误信息。

  • data: 包含实际返回的数据。在成功的响应中，这里可能是请求的数据对象或数据集合。

• 优点:

  • 标准化: 使得API的响应格式统一，简化客户端的处理逻辑。

  • 易于调试: 通过状态码和消息，可以快速识别请求是否成功以及失败的原因。

  • 扩展性: 方便添加额外的信息，如时间戳、分页信息等，而不影响现有逻辑。

• 示例:

  {"code": 200,"msg": "操作成功","data": {// 实际的数据对象}
  }

  这个JSON对象是一个典型的统一响应结果示例，它清晰地表明了操作的状态和返回的数据。

这篇关于SpingBoot快速入门下的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---