本文主要是介绍通信系统的最佳线性均衡器(1)---维纳滤波线性均衡,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本篇文章是博主在通信等领域学习时,用于个人学习、研究或者欣赏使用,并基于博主对通信等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在通信领域笔记:
通信领域笔记(4)---《通信系统的最佳线性均衡器(1)---维纳滤波线性均衡》
通信系统的最佳线性均衡器(1)---维纳滤波线性均衡
目录
1. 背景分析
2 理论分析推导
3 MATLAB 仿真 FIR 最佳线性滤波器
4 总结分析
1. 背景分析
在通信系统中,发射机发送的信号通过信道传输到接收机,传输信道有不同 的媒体,主要分成有线和无线两类。以无线为例,发射信号通过无线信道传播, 经过多径到达接收机而被接收,这些多径是由于信道中的信号经反射、折射和衍射形成的。多径传播产生的接收信号是由多个延迟衰落的发射信号叠加而成的。因此接收机接收到的信号中存在着串扰和畸变,直接进行检测会产生较大的误码。一种改善信号检测性能的装置是信道均衡器,它的目标是补偿信道造成的串扰和畸变。通信系统的最佳线性均衡器通常是指使用线性滤波器来抵消信道引起的失真和干扰,以尽可能恢复发送端发送的信号。最佳的线性均衡器设计需要考虑到信道的特性以及发送信号的统计特性。一种常见的实现方式是使用维纳-霍夫等式,它可以得到一个最小均方误差的解。另外,常用的线性均衡器包括莱斯滤波器、线性均衡器和决策反馈均衡器等。
维纳滤波器是一种最佳线性无失真滤波器,它的设计考虑了信道的特性和发送信号的统计特性,以最小化输出信号与原始信号之间的均方误差。因此,维纳滤波器可以用作通信系统中的线性均衡器,帮助抵消信道引起的失真和干扰。考虑一个简化的线性自适应均衡器的原理性实验框图如图 1 所示。随机数据产生器产生双极性的随机序列𝑠(𝑛),它随机地取±1。随机信号通过一个信道传输,信道性质可由一个三系数 FIR 滤波器近似,滤波器系数分别是 0.3,0.9,0.3。在信道输出端加入方差为𝜎 2的高斯白噪声。设计一个有 11 个权系数的 FIR 结构的维纳滤波器作为本问题的均衡器,为使均衡器的权系数接近对称,令均衡器的期望响应为𝑠(𝑛 − 7)。在几个选定的信噪比下,进行实验。
2 理论分析推导
在维纳滤波器设计中,最常用的是 FIR 维纳滤波器。这是因为 FIR 滤波器具有稳定性和实现上的优势,其设计更为直观和容易控制。此外,FIR 滤波器可以 较为灵活地满足各种滤波要求,并且不会引入稳定性和因果性方面的问题。相比 之下,因果 IIR 和非因果 IIR 维纳滤波器在实际设计中使用较少,因为其设计和实现更为复杂,对系统稳定性和实时性要求较高。此处以 FIR 维纳滤波器为例进 行分析。 已知𝒚(𝒏)是期望的输出信号,𝒙(𝒏)是输入信号,𝒆(𝒏)是误差信号。𝒚(𝒏)和𝒙(𝒏) 是均值为 0 的平稳的离散时间信号,二阶矩已知。
2.1 维纳-霍夫方程(Wiener-Hopf 方程)

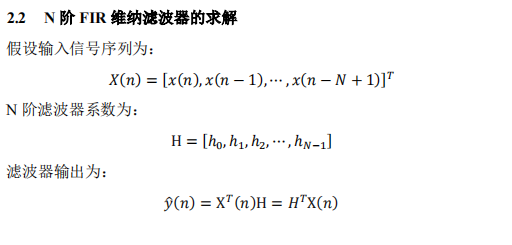
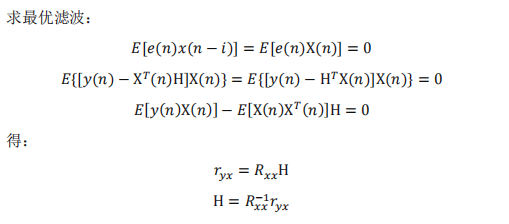
3 MATLAB 仿真 FIR 最佳线性滤波器
首先生成双极性随机序列𝑠(𝑛),通过模拟信道特性的三系数 FIR 滤波器,并添加信噪比为 20dB 的高斯白噪声,得到维纳滤波器的输入信号序列𝑥(𝑛),期望 信号为原始双极性随机序列𝑠(𝑛)。
clc
clear all
close all
% 生成双极性随机序列s(n)
N = 500;
s = sign(randn(1, N));% 模拟信号通过信道传输
h = [0.3, 0.9, 0.3]; % FIR滤波器系数
x = filter(h, 1, s); % 信号通过FIR滤波器
x = x(2:end);
SNR_dB = 10; % 信噪比为10dB
r = awgn(x,SNR_dB,'measured');%信号加入高斯白噪声信号
figure
plot(s(1:200));
hold on
plot(r(1:200));
legend('双极性随机序列s(n)','加噪后信号x(n)');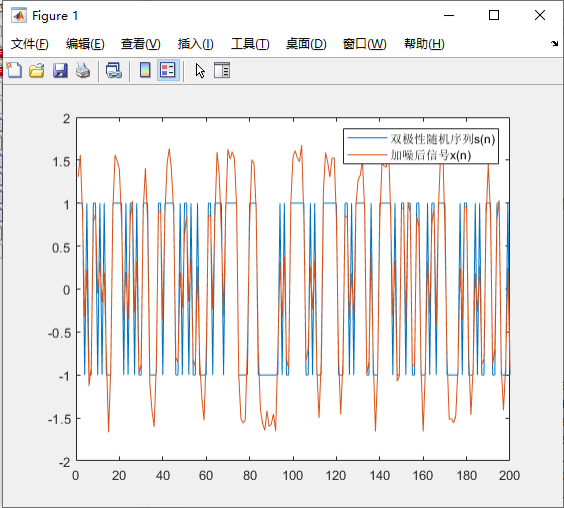
%%FIR最佳线性滤波器
Rx = xcorr(r,10);%输入自相关
Rxyd = xcorr(r,s,10);%输入与期望输出的互相关
R0=[Rx(10) Rx(11) Rx(12) Rx(13) Rx(14) Rx(15) Rx(16) Rx(17) Rx(18) Rx(19) Rx(20) Rx(21);Rx(11) Rx(10) Rx(11) Rx(12) Rx(13) Rx(14) Rx(15) Rx(16) Rx(17) Rx(18) Rx(19) Rx(20);Rx(12) Rx(11) Rx(10) Rx(11) Rx(12) Rx(13) Rx(14) Rx(15) Rx(16) Rx(17) Rx(18) Rx(19);Rx(13) Rx(12) Rx(11) Rx(10) Rx(11) Rx(12) Rx(13) Rx(14) Rx(15) Rx(16) Rx(17) Rx(18);Rx(14) Rx(13) Rx(12) Rx(11) Rx(10) Rx(11) Rx(12) Rx(13) Rx(14) Rx(15) Rx(16) Rx(17);Rx(15) Rx(14) Rx(13) Rx(12) Rx(11) Rx(10) Rx(11) Rx(12) Rx(13) Rx(14) Rx(15) Rx(16);Rx(16) Rx(15) Rx(14) Rx(13) Rx(12) Rx(11) Rx(10) Rx(11) Rx(12) Rx(13) Rx(14) Rx(15);Rx(17) Rx(16) Rx(15) Rx(14) Rx(13) Rx(12) Rx(11) Rx(10) Rx(11) Rx(12) Rx(13) Rx(14);Rx(18) Rx(17) Rx(16) Rx(15) Rx(14) Rx(13) Rx(12) Rx(11) Rx(10) Rx(11) Rx(12) Rx(13);Rx(19) Rx(18) Rx(17) Rx(16) Rx(15) Rx(14) Rx(13) Rx(12) Rx(11) Rx(10) Rx(11) Rx(12);Rx(20) Rx(19) Rx(18) Rx(17) Rx(16) Rx(15) Rx(14) Rx(13) Rx(12) Rx(11) Rx(10) Rx(11);Rx(21) Rx(20) Rx(19) Rx(18) Rx(17) Rx(16) Rx(15) Rx(14) Rx(13) Rx(12) Rx(11) Rx(10);];
R1=[Rxyd(10) Rxyd(11) Rxyd(12) Rxyd(13) Rxyd(14) Rxyd(15) Rxyd(16) Rxyd(17) Rxyd(18) Rxyd(19) Rxyd(20) Rxyd(21)]';
h = (R0\R1);%滤波器系数
out_signal = filter(h, 1, r);%输出信号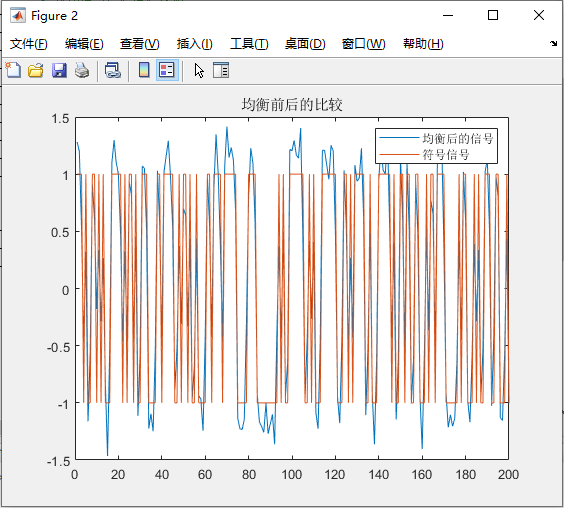
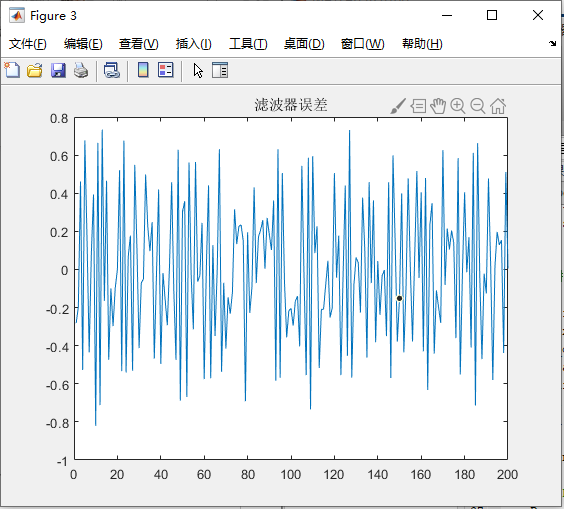
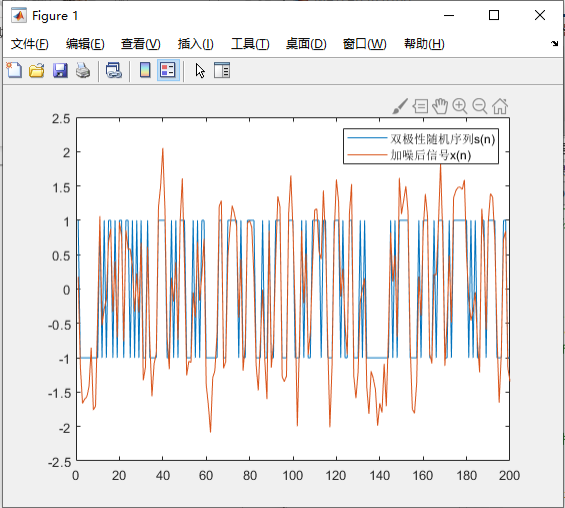
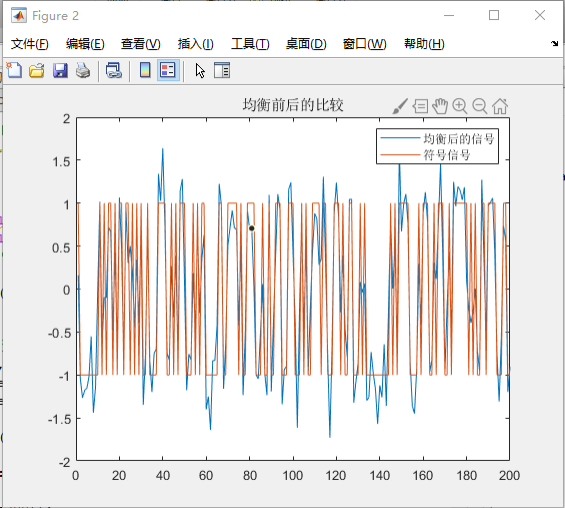
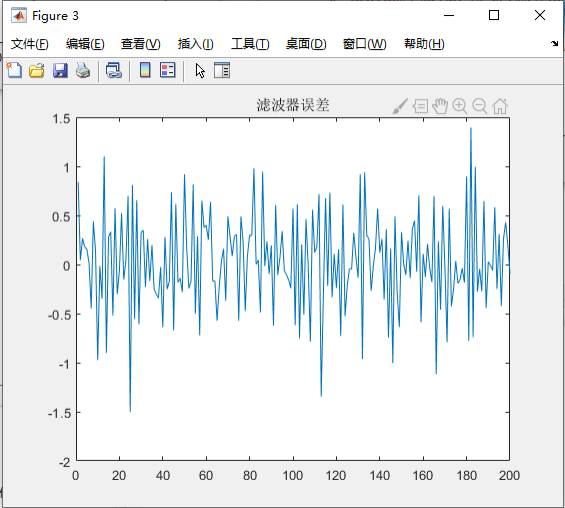
由图知,减小信噪比后,加噪后信号波动变大,滤波器误差随着信噪比的减小而增大了,效果并不出众。由于 FIR 最佳线性滤波器计算得到的滤波器参数只是使用了 12 个输出序列进行运算,并没有进行迭代过程,故计算出的滤波器参数并不是最优的,因此考虑使用自适应滤波器的方法来滤除高斯噪声。(此处只是提前使用自适应算法,改进滤波效果,具体自适应算法的实验在 3.2)
在 20dB 的信噪比下,利用 LMS 自适应滤波器进行实验,
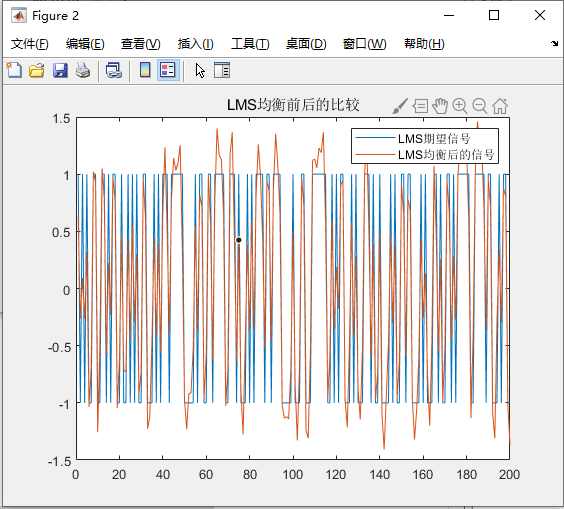
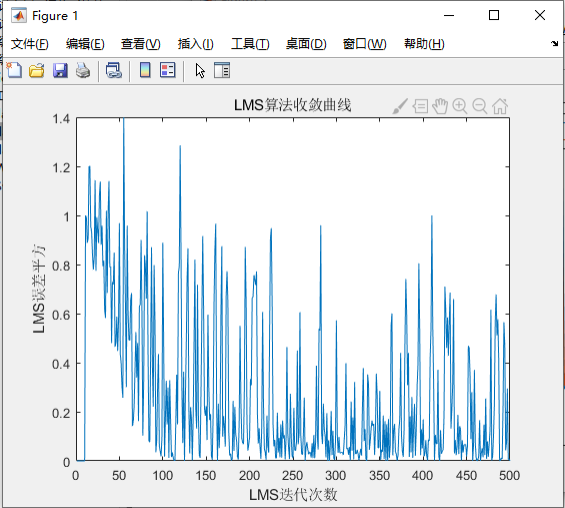
由上图可知,LMS 自适应算法的误差曲线处于收敛趋势,且进行到大约 250 次迭代时,误差曲线基本收敛。与 FIR 最佳线性滤波器相比,均衡后的信号序列更加贴近期望信号,效果更好。
4 总结分析
维纳滤波器与常规滤波器相比,在抑制信道失真和噪声方面表现出良好的效果。但在动态信道或噪声较大的通信系统,维纳滤波器的效果会减弱。在算法设计上,需要注意信号时刻对齐的问题。
文章若有不当和不正确之处,还望理解与指出。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请联系博主删除。如有错误、疑问和侵权,欢迎评论留言联系作者,或者私信联系作者。
这篇关于通信系统的最佳线性均衡器(1)---维纳滤波线性均衡的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





