本文主要是介绍#01算法的复杂性,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
时间复杂度
public void print(int n){int a = 1; //执行1次for(int i=0;i<n;++i){//执行n次System.out.println(a+i);//执行n次}
}该算法的时间复杂度是O(2n+1) 大O会忽略常数、低阶和系数,最终记作O(n); 如果算法的执行时间和数据规模n无关,则是常量阶,记作O(1);
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)

指数和阶乘是非多项式量级,其余都是多项式量级。我们把时间复杂度是非多项式量级的算法问题称为NP(Non-Deterministic-Polynomial,非确定多项式)问题。
//n是数组nums的长度
public int find(int[]nums,int n,int target){for(int i=0;i<n;++i){if(nums[i]==target){return i;}}return -1;
}
最好情况:上边最理想的情况就是第一个就是要找的,所以最好情况下时间复杂度是O(1)
最坏情况:最坏的情况,就是要找的数在最后一个,需要遍历n次,最坏情况下时间复杂度是O(n
平均时间复杂度:为了方便说明,我们假设数组中一定存在要找的数。而要找的数在0 - n-1这些位置出现的概率相同,都是 1/n ,所以考虑每种情况下总共要查找的次数,求出总数,然后再除以 可能的情况数,就是平均要查找的次数:

去除常量和系数就是:O(n) ;
public int[] twoSum(int[] nums, int target) {//初始化一个数组存放结果int[] re =new int[2];for(int i=0;i<nums.length-1;++i){int num1 = nums[i];for(int j=i+1;j<nums.length;++j){int nums2=nums[j];//如果找到,就返回结果,避免多余循环if((num1+nums2)==target){re[0] = i;re[1] = j;return re;}}}return re;}
最好情况:最好情况就是我们要找的两个数,刚好就是第一个和第二个数。所以外循环循环一次,内循环循环一次就完成了查找。时间复杂度是:O ( 1 ) ;
最坏情况:最坏情况就是,找遍到最后一个元素,才找到。
- 外层循环是从0循环到n-2
- 内层循环和外层循环的值有关,从外层当前的值,循环到n-1
总的比较次数就是每个外层循环时,内层循环的次数之和。比如外层i=0时,内层从1循环到n-1循环了n-1次,外层i=1时,内层从2循环到n-1循环了n-2次 …直到最后一次,内层只需要循环1次...

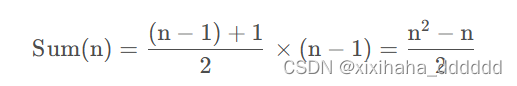
去掉常量、系数和低阶,时间复杂度就是: O() ;
平均情况 :
分析:我们最终的目的是要找到两个数,满足我们的条件。代码的外层循环显然是找第一个数,内层循环在找第二个数。根据假设,这对数存在并且唯一。(其他情况,比如有重复,复杂度会介于最好和平均之间,因为更容易找到,所以这里我们只分析唯一的情况)我们假设第一个要找的数 出现在下标 0 - n -2 的概率相等,都是 1/(n-2) , 所以外层循环的次数可能出现的情况如下:
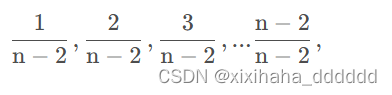
当外层循环的次数是 1/(n-2) 时,内层需要循环n-1次,因为内层循环次数和外层的当前i有关。所以加权平均情况下的总的比较次数就是:


分子和分母的n-1 与n-2可以近似约掉,最后去掉系数和低阶 所以最终结果就是: O() ;
int i = 1;
while(i<n)
{i = i * 2;
}
在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。我们试着求解一下,假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2^n
也就是说当循环 log2^n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(logn)
计算时间复杂度
例1
//计算Func1的时间复杂度
void Func1(int N)
{int count = 0;for (int i = 0; i < 2 * N; i++){for (int j = 0; j < 2 * N; j++){count++;}}for (int k = 0; k < 2 * N; k++){count++;}
}
所以Func1函数的时间复杂度为:T(N) = 4 * + 2 * N ;大O的渐进表示法,只保留最高阶项(即4 *
),去除最高项的系数后(即
)。所以,用大O的渐进表示法表示Func1函数的时间复杂度为:O(
) 。
例2
//计算Func2的时间复杂度
void Func2(int N)
{int count = 0;for (int k = 0; k < 100; k++){++count;}printf("%d\n", count);
}
Func2函数的时间复杂度为T(N) = 100 ;根据大O的渐进表示法,所有的常数都用常数1来表示,所以,用大O的渐进表示法表示Func2函数的时间复杂度为:O(1) ;
例3
//计算二分查找函数的时间复杂度
int BinarySearch(int* a, int N, int x)
{assert(a);int begin = 0;int end = N - 1;while (begin < end){int mid = begin + ((end - begin) >> 1);if (x > a[mid])begin = mid + 1;else if (x < a[mid])end = mid - 1;elsereturn mid;}return -1;
}
计算二分查找函数的时间复杂度,我们需要对代码进行分析:我们用二分查找法查找数据时,查找一次后可以筛去一半的数据,经过一次次的筛选,最后会使得待查数据只剩一个,那么我们查找的次数就是while循环执行的次数。
因为数据个数为N,一次查找筛去一半的数据,即还剩N/2个数据,经过一次次的筛选,数据最后剩下1个,那么查找的次数可以理解为N除以若干个2,最后得1,那么while循环执行的次数就是N除以2的次数,我们只需计算N除以了多少次2最终等于1即可。

我们假设N除以了x个2,最终等于1,那么

最后,两边同时取2的对数,得while循环执行的次数,即x = logN 。所以,用大O的渐进表示法表示二分查找函数的时间复杂度为:O(logN)
表示时间和空间复杂度时,log表示以2为底的对数。
例4
//计算斐波那契函数的时间复杂度
int Fibonacci1(int N)
{if (N == 0||N == 1)return 1;elsereturn Fibonacci1(N - 1) + Fibonacci1(N - 2);
}
使用递归法求斐波那契数,当我们要求某一个斐波那契数时,需要知道他的前两个斐波那契数,然后相加得出。那么当我们要知道第N个斐波那契数时,递归的次数如下图:

因为右下角的递归函数会提前结束,所以图中三角形必定有一块是没有数据的,但是当N趋于无穷时,那缺省的一小块便可以忽略不计,这时总共调用斐波那契函数的次数为:

等比数列的求和,最后得出结果为: - 1 。
保留最高阶项后,用大O的渐进表示法表示斐波那契函数的时间复杂度为:O() 。
注:递归算法的时间复杂度 = 递归的次数 * 每次递归函数中的次数。
//注意:斐波那契数列自顶向下递归的时间复杂度是2的n次方/(1.618的n次方);空间复杂度是O(n) ; 自底向上保留子问题的值求解时间复杂性是O(n),空间复杂度也是O(n);

空间复杂度
O(1)
一个算法的空间复杂度(Space Complexity)S(n)定义为该算法所耗费的存储空间,它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。空间复杂度算的是变量的个数。
如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可表示为 O(1)
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
//代码中的 i、j、m 所分配的空间都不随着处理数据量变化,因此它的空间复杂度S(n) = O(1)O(n)
int[] m = new int[n]
for(i=1; i<=n; ++i)
{j = i;j++;
}
第一行new了一个数组出来,这个数据占用的大小为n,这段代码的2-6行,虽然有循环,但没有再分配新的空间,因此,这段代码的空间复杂度主要看第一行即可,即 S(n) = O(n)
例1
//计算冒泡排序函数的空间复杂度
void BubbleSort(int* a, int N)
{assert(a);for (int i = 0; i < N; i++){int exchange = 0;for (int j = 0; j < N - 1 - i; j++){if (a[j]>a[j + 1]){int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;exchange = 1;}}if (exchange == 0)break;}
}
冒泡排序函数中使用了常数个额外空间(即常数个变量),所以用大O的渐进表示法表示冒泡排序函数的空间复杂度为O(1) 。
例2
//计算阶乘递归函数的空间复杂度
long long Factorial(size_t N)
{return N < 2 ? N : Factorial(N - 1)*N;
}
阶乘递归函数会依次调用Factorial(N),Factorial(N-1),…,Factorial(2),Factorial(1),开辟了N个空间,所以空间复杂度为O(N) 。
注:递归算法的空间复杂度通常是递归的深度(即递归多少层)。
例3
斐波那契数列的空间复杂性为O(n);
这篇关于#01算法的复杂性的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








