Attention Is All You Need详解

本文主要是介绍Attention Is All You Need详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一.背景。

在此模型之前，序列到序列的任务（如机器翻译、文本摘要等）通常采用循环神经网络（RNN）或卷积神经网络（CNN）。然而，RNN 在处理长距离依赖时存在一定的局限性（举个例子：处理第K_t个词时，需要用到K₁到K_t-1的词的输出作为输入），训练时也比较耗时。而 CNN 在处理序列数据时难以捕捉到全局的依赖关系。然而这篇文章介绍的模型Transformer完全基于注意力机制，与CNN，RNN，LSTM模型对比更加简单并且高效。

二.模型架构。

Transformer 模型采用了编码器-解码器架构。先上一个论文里面的架构图，再逐步介绍其中的各个部分。
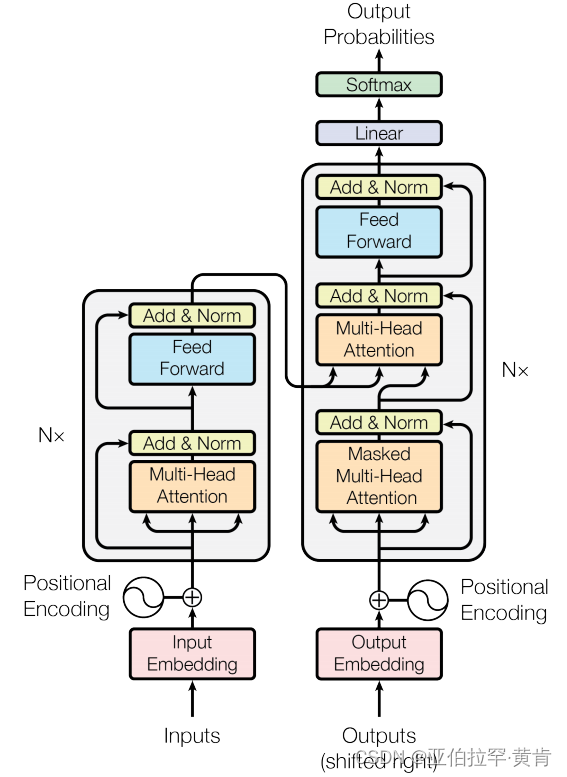
在这里插入图片描述

1.Embedding

在这里插入图片描述

Embedding是什么：

为了对字符进行计算，我们首先需要将字符（或单词）转换成一种数值表示形式。独热编码（One-Hot Encoding）是一种常用的方法之一，例如词汇表 {'猫': 0, '狗': 1, '苹果': 2} （此处的索引012一般是根据某个词典获得，即某词典0号索引处为单词‘猫’），‘ 猫’ 的独热编码就是 [1, 0, 0] ，‘狗’ 的独热编码就是 [0, 1, 0]，但是这样的缺点就是向量维度高且稀疏，计算效率低。如果词汇表有 10,000 个单词，那么每个独热向量的维度就是 10,000，并且是稀疏的，即大部分元素都是 0，只有一个位置是 1。
所以在深度学习特别是自然语言处理（NLP）中，我们通常会采用更加高效的嵌入表示（Embedding）。通过Embedding，每个字符（或单词）被表示为一个低维的密集向量。这些向量是通过训练得到的，可以捕捉字符（或单词）之间的语义关系。例如通过嵌入层，单词“猫”可能被表示为一个 5 维（维数由我们定义）向量 [0.0376, -0.2343, 0.1655, -0.0053, 0.1353] 。可见其特点是维度低且密集，计算效率高，并且能够捕捉语义信息。

Embedding的例子：

在 PyTorch 中，有一个函数torch.nn.Embedding(num_embedings, embedding_dim)，其中 num_embedding 表示词表总的长度，embedding_dim 表示单词嵌入的维度，此函数会创建一个嵌入矩阵（通常是随机的），其形状为 (num_embedding , embedding_dim)，给定输入张量（通常是单词索引），其形状为(batch_size, sequence_length)，该层会将每个索引映射到对应的嵌入向量，返回一个形状为 (batch_size, sequence_length, embedding_dim) 的张量。
以下是例子代码：

import torch
import torch.nn as nn# 定义词汇表大小和嵌入向量维度
vocab_size = 10 #词汇表大小
embedding_dim = 5 #向量维度# 创建嵌入层
embedding_layer = nn.Embedding(num_embeddings=vocab_size, embedding_dim=embedding_dim)# 输入张量（单词索引）
input_tensor = torch.tensor([[1, 2, 3], [4, 5, 6]], dtype=torch.long)  # 示例输入，形状为 (batch_size, sequence_length)# 通过嵌入层得到嵌入向量
embedding_output = embedding_layer(input_tensor)print(f"Input Tensor Shape: {input_tensor.shape}")
print(f"Embedding Output Shape: {embedding_output.shape}")
print(f"Embedding Output:\n{embedding_output}")
'''
输出:
Input Tensor Shape: torch.Size([2, 3])
Embedding Output Shape: torch.Size([2, 3, 5])
Embedding Output:
tensor([[[ 0.0069,  0.0465, -0.0205,  0.0080, -0.0114],[-0.0244,  0.0404,  0.0452, -0.0027, -0.0307],[ 0.0024, -0.0043,  0.0340,  0.0370, -0.0400]],[[ 0.0057, -0.0015, -0.0154, -0.0306, -0.0375],[ 0.0317, -0.0275,  0.0160,  0.0283,  0.0040],[-0.0331, -0.0061,  0.0452,  0.0484, -0.0350]]], grad_fn=<EmbeddingBackward0>)
'''

Transformer中的Embedding

论文原文：（在嵌入层中，我们将这些权重乘以√dmodel）
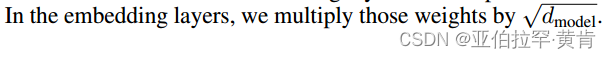
在这里插入图片描述

在Embedding中使用 math.sqrt(self.d_model)（即 $\sqrt[]{d}$ ）进行缩放，是在实际实现中的一种实践，可以保持数值稳定性，确保在随后的计算中，尤其是在与模型其他部分进行交互时，不会出现数值过大或过小的问题。

数学解释：

以下是复现代码：（这里暂定input跟output的Embedding是一样的）

class Embedding(nn.Module):def __init__(self, vocab_size, d_model):# vocab_size:词表长度    d_model:嵌入维度super(Embedding, self).__init__()self.embedding = nn.Embedding(vocab_size, d_model)self.d_model = d_modeldef forward(self, x):# x:输入张量# 乘以 根号dk 保持数据稳定性 return self.embedding(x) * math.sqrt(self.d_model)

2.Positional Encoding

在这里插入图片描述

为什么需要Positional Encoding

论文原文：（由于我们的模型不包含递归和卷积，为了使模型利用序列的顺序，我们必须注入一些关于序列中标记的相对或绝对位置的信息）
在这里插入图片描述
也就是attention没有时序信息，需要我们自己加入。（RNN的做法是上一个时刻的输出作为此时刻的输入以此引入时序信息）

Positional Encoding的实现

论文原文：
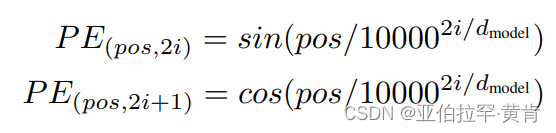
在这里插入图片描述

其中，pos 即 position，意为 token 在句中的位置，i为向量的某一维度。借助此公式再结合三角函数的性质
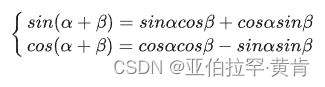
在这里插入图片描述
可以得到：

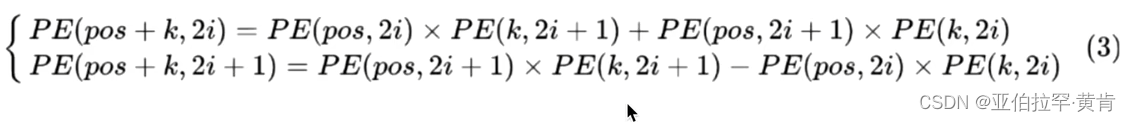
可以看出，对于 pos+k 位置的位置向量某一维 2i 或 2i+1 而言，可以表示为，pos 位置与k位置的位置向量的2i与 2i+1维的线性组合，这样的线性组合意味着位置向量中蕴含了相对位置信息。具体可以参考视频讲解。
以下是复现代码：

class PositionalEncoding(nn.Module):def __init__(self, d_model, dropout=0.1, max_len=5000):'''初始化函数，三个参数分别是：d_model:词嵌入维度； dropout：置0比率（位置编码与输入嵌入相加后一起作为模型的输入。模型在学习过程中会学习如何利用这些位置信息。如果位置编码没有经过 dropout 的正则化处理，模型可能会过度依赖这些位置信息，从而对训练数据记忆过深，导致在处理未见数据时表现不佳。）max_len:每个句子的最大长度。'''super(PositionalEncoding, self).__init__()#实例化dropout层，并传入参数self.dropout = nn.Dropout(p=dropout)#初始化一个位置编码矩阵，全为0，大小是max_len * d_modelpe = torch.zeros(max_len, d_model)#初始化一个绝对位置矩阵，词的绝对位置即索引位置position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)#接下来就是把位置信息加入到位置编码矩阵中去，也就是把max_len * 1的position绝对位置矩阵变换成max_len * d_model形状，然后覆盖初始矩阵#也就是max_len * 1 的矩阵去乘以一个 1 * d_modl 的变换矩阵div_term，然后再进行覆盖，这里因为位置编码可以分成奇数和偶数两部分，故可以将变换矩阵更改为 1 * （d_model / 2）的形状div_term = torch.exp(torch.arange(0, d_model, 2).float() * -(math.log(10000.0) / d_model))#按照公式给位置编码进行赋值pe[:, 0::2] = torch.sin(position * div_term)pe[:, 1::2] = torch.cos(position * div_term)#这样子就得到了位置编码矩阵pe，但是要和embedding的输出相加就必须拓展一个维度pe = pe.unsqueeze(0)#因为无论我们输入的是什么，这个位置编码都不会改变，也就是所有的输入是公用一个位置编码的，所以这边使用self.register_buffer，其是一个用于将张量注册为模型的一部分的方法。它的主要用途是注册一些不作为模型参数的持久状态，例如在训练和推理过程中不需要更新的固定数据。self.register_buffer('pe', pe)def forward(self,x):#因为一个句子有长有短，所以可以位置编码只截取到句子的实际长度即可。x = x + self.pe[:, :x.size(1)]#最后使用dropout防止过拟合，并返回结果。return self.dropout(x)

实际例子

通过一个超参数比较小的例子输出并展示还是比较容易理解每一步骤的做法的。

import torch
import torch.nn as nn
import mathmax_len = 10
d_model = 6# 初始化位置编码矩阵
pe = torch.zeros(max_len, d_model)
print(pe)
'''
tensor([[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0.]])
'''# 初始化绝对位置矩阵
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
print(position)
'''
tensor([[0.],[1.],[2.],[3.],[4.],[5.],[6.],[7.],[8.],[9.]])
'''# 计算变换矩阵 div_term
div_term = torch.exp(torch.arange(0, d_model, 2).float() * -(math.log(10000.0) / d_model))
print(div_term)
'''
Div term matrix:
tensor([1.0000, 0.0464, 0.0022])
'''
# 计算位置编码矩阵
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
print(pe)
'''
tensor([[ 0.0000,  1.0000,  0.0000,  1.0000,  0.0000,  1.0000],[ 0.8415,  0.5403,  0.0464,  0.9989,  0.0022,  1.0000],[ 0.9093, -0.4161,  0.0927,  0.9957,  0.0043,  1.0000],[ 0.1411, -0.9900,  0.1388,  0.9903,  0.0065,  1.0000],[-0.7568, -0.6536,  0.1846,  0.9828,  0.0086,  1.0000],[-0.9589,  0.2837,  0.2300,  0.9732,  0.0108,  0.9999],[-0.2794,  0.9602,  0.2749,  0.9615,  0.0129,  0.9999],[ 0.6570,  0.7539,  0.3192,  0.9477,  0.0151,  0.9999],[ 0.9894, -0.1455,  0.3629,  0.9318,  0.0172,  0.9999],[ 0.4121, -0.9111,  0.4057,  0.9140,  0.0194,  0.9998]])
'''#最后再添加一个维度
pe = pe.unsqueeze(0)
print(pe)
'''
tensor([[[ 0.0000,  1.0000,  0.0000,  1.0000,  0.0000,  1.0000],[ 0.8415,  0.5403,  0.0464,  0.9989,  0.0022,  1.0000],[ 0.9093, -0.4161,  0.0927,  0.9957,  0.0043,  1.0000],[ 0.1411, -0.9900,  0.1388,  0.9903,  0.0065,  1.0000],[-0.7568, -0.6536,  0.1846,  0.9828,  0.0086,  1.0000],[-0.9589,  0.2837,  0.2300,  0.9732,  0.0108,  0.9999],[-0.2794,  0.9602,  0.2749,  0.9615,  0.0129,  0.9999],[ 0.6570,  0.7539,  0.3192,  0.9477,  0.0151,  0.9999],[ 0.9894, -0.1455,  0.3629,  0.9318,  0.0172,  0.9999],[ 0.4121, -0.9111,  0.4057,  0.9140,  0.0194,  0.9998]]])
'''