1.1. 大数定律-独立性

本文主要是介绍1.1. 大数定律-独立性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

独立性

1. 独立性的定义
- 1.1. 两个事件、两个随机变量、两个 $\sigma$ -代数独立
- 1.2. 多事件、多个 $\sigma$ -代数、多个随机变、多个事件独立
- 1.3. 成对独立和独立的关系
2. 独立性的充分条件
3. 独立向量的分布和期望
- 3.1. 独立向量的分布
- 3.2. 独立随机变量乘积期望
- - 3.2.1. 独立的随机变量意味着不相关
  - 3.2.2. 独立随机变量和的分布
4. 独立随机变量的存在性
- 4.1. 有限个独立随机变量的构造
- 4.2. 无穷个独立随机变量的构造

本文主要介绍概率极限理论中的大数定律,内容包括:

Chebyshev弱大数定律, 三角阵列的弱定律(截断方法)得到的Khinchin弱大数定律;
强大数定律的两种证明方法: 由Borel-Cantelli引理得到的强大数定律, 随机级数收敛方法得到的强大数定律. 此外给出了更新理论和大偏差理论.

1. 独立性的定义

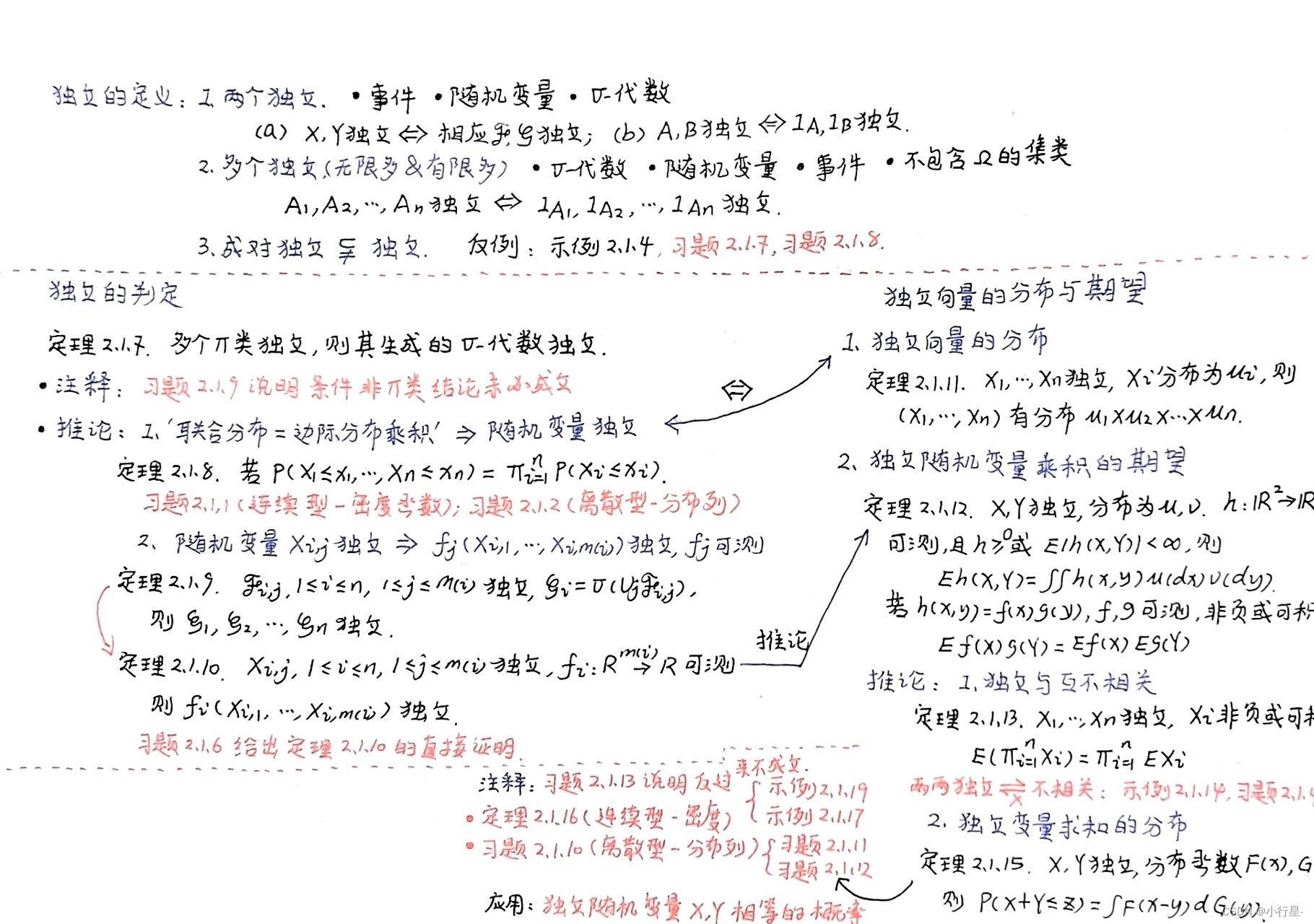
在这里插入图片描述
概率论与测度论的分水岭: 引入条件概率与独立性这两个概念意味着测度论的终结, 概率论的开始.测度论是研究概率的一种工具(例如可以用纯代数的方法研究概率:Free probability), 因此概率论中最重要的概念本质上不依赖于测度. 下面是本节-独立性的思维导图.

两个事件独立,两个随机变量独立,两个 $\sigma$ -代数独立的定义; 三者之间的关联:4. 两个事件独立是两个随机变量独立的特殊情况(定理2.1.2); 2. 两个随机变量独立是两个 $\sigma$ -代数独立的特殊情况(定理 2.1.1).
多个事件独立,多个随机变量独立,多个 $\sigma$ -代数独立的定义;三者之间的关联:
多个随机变量独立是多个 $\sigma$ -代数独立的特殊情况(定理2.1.3).

1.1. 两个事件、两个随机变量、两个 $\sigma$ -代数独立

定义 (两个事件、两个随机变量、两个 $\sigma$ -代数独立)

(i) 若 $\cap B)=P(A) P(B)$ ,则两个事件 $A$ 和 $B$ 是独立的;\
(ii) 两个随机变量 $\mathrm{X}$ 和 $\mathrm{Y}$ 是独立的, 如果对于所有的 $\in R$
$\in C, Y \in D)=P(X \in C) P(Y \in D)$
即事件 $A=\{X \in C\}$ 和 $B=\{Y \in D\}$ 是独立的.\
(iii) 若对所有 $\in \mathscr{F}$ , $\in \mathscr{G}$ , 事件 $A$ 和 $B$ 都是独立的, 则两个 $\sigma$ -代数 $\mathscr{F}$ , $\mathcal{G}$ 独立.

定理2.1.1 (随机变量独立与 $\sigma$ 代数独立的关系)]

(i) 若 $X$ , $Y$ 独立, 则 $\sigma(\mathrm{X})$ , $\sigma(\mathrm{Y})$ 独立.
(ii) 若 $\mathscr{F}$ , $\mathscr{G}$ 独立, $X\in\mathcal{F}$ , $Y\in\mathcal{G}$ , $X$ , $Y$ 独立.

证明：根据定义证明即可.

定理 2.1.2 (事件独立与随机变量独立的关系)

(i) 若 $A$ , $B$ 独立, 则 $A^{c}$ 和 $B$ , $A$ 和 $B^{c}$ , $A^{c}$ 和 $B^{c}$ 也独立.\
(ii) 相反,事件 $A$ 和 $B$ 独立, 当且仅当它们的示性随机变量 $1_{A}$ , $1_{B}$ 独立.

将其简化为有限多对象的情况,即如果每个有限子集合中的对象都独立,那么无限集合中的对象( $\sigma$ 代数、随机变量或集合)就是独立的.

1.2. 多事件、多个 $\sigma$ -代数、多个随机变、多个事件独立

定义 (无穷多事件、多个 $\sigma$ -代数、多个随机变、多个事件独立)
(i) 多个 $\sigma$ -代数 $\mathcal{F}_{1}, \mathcal{F}_{2}, \ldots, \mathcal{F}_{n}$ 独立,如果任意 $A_{i} \in \mathcal{F}_{i} ,$ 对 $\ldots, n$ ,有
$P\left(\cap_{i=1}^{n} A_{i}\right)=\prod_{i=1}^{n} P\left(A_{i}\right)$
(ii) 随机变量 $X_{1}, \ldots, X_{n}$ 独立,如果对 $\ldots, n$ ,任意 $B_{i} \in \mathcal{R}$ 有
$P\left(\cap_{i=1}^{n}\left\{X_{i} \in B_{i}\right\}\right)=\prod_{i=1}^{n} P\left(X_{i} \in B_{i}\right)$
(iii) 集合 $A_{1}, \ldots, A_{n}$ 独立如果任意 $\subset\{1, \ldots n\}$ 有 $P\left(\cap_{i \in I} A_{i}\right)=\prod_{i \in I} P\left(A_{i}\right)$ .

定理2.1.3 (多个事件独立与多个随机变量独立的关系) 令 $A_{1}, A_{2}, \ldots A_{n}$ 独立. (i) $A_{1}^{c}, A_{2}, \ldots, A_{n}$ 是独立的; (ii) $1_{A_{1}}, \ldots, 1_{A_{n}}$ 是独立.

1.3. 成对独立和独立的关系

示例2.1.4与习题2.1.7,习题2.1.8):独立的事件是成对独立的,而相反是不正确的 三个随机变量独立,而有了第四个不独立的例子.

2. 独立性的充分条件

证明多个随机变量独立等价于联合分布等于边际分布的乘积.

为证明随机变量X和Y是独立的,必须检查所有Borel集合A和B独立,直接证明过于繁琐,有必要给出一些充分性条件(定理2.1.7).

引理2.1.5 (sigma代数并上全集后的独立性) 集类 $\mathcal{A}_{1} \cup\{\Omega\}, \mathcal{A}_{2} \cup\{\Omega\}, \ldots, \mathcal{A}_{n} \cup\{\Omega\} \subset \mathcal{F}$ 独立,对任意 $A_{i} \in \mathcal{A}_{i}$ ,
$P\left(\cap_{i=1}^{n} A_{i}\right)=\prod_{i=1}^{n} P\left(A_{i}\right)$

定理2.1 .7 (各独立pi类生成的sigma代数独立) 假设 $\mathcal{A}_{1}, \mathcal{A}_{2}, \ldots, \mathcal{A}_{n}$ 独立,任意 $\mathcal{A}_{i}$ 是 $\pi$ 类. 则 $\sigma\left(\mathcal{A}_{1}\right), \sigma\left(\mathcal{A}_{2}\right), \ldots, \sigma\left(\mathcal{A}_{n}\right)$ 独立.

习题2.1.9 两个集类独立,生成的 $\sigma$ 代数不独立

推论2.1 .8 (随机变量独立只需分布函数独立性) 为让 $X_{1}, \ldots, X_{n}$ 独立,只要对所有 $x_{1}, \ldots, x_{n} \in(-\infty, \infty]$ 有
$P\left(X_{1} \leq x_{1}, \ldots, X_{n} \leq x_{n}\right)=\prod_{i=1}^{n} P\left(X_{i} \leq x_{i}\right)$

习题2.1.1和2.1.2 密度函数和离散随机变量的独立性

假设 $X_{1}, \ldots, X_{n}$ 是独立随机变量,且 $X_{i}$ 有分布 $\mu_{i}$ ,则 $\left(X_{1}, \ldots, X_{n}\right)$ 有分布 $\mu_{1} \times \cdots \times \mu_{n}$ .

3. 独立向量的分布和期望

首先给出第一节【独立性的第二个判定方法】(第一个判别法推论),即独立随机变量的不相交集合的函数是独立的(定理2.1.10),以此证明两个独立的随机变量意味着不相关(定理2.1.12,定理2.1.13),不过互不相关的随机变量不一定相互独立.

3.1. 独立向量的分布

引理 2.1.9 假设 $\mathcal{F}_{i, j}, 1 \leq i \leq n, 1 \leq j \leq m(i)$ 独立,令 $\mathcal{G}_{i}=\sigma\left(\cup_{j} \mathcal{F}_{i, j}\right)$ . 则 $\mathcal{G}_{1}, \ldots, \mathcal{G}_{n}$ 独立.

定理 2.1.10(独立随机变量的不相交集合的函数独立) 若 $\leq i \leq n, 1 \leq j \leq m(i), X_{i, j}$ 独立, $f_{i}: \mathbf{R}^{m(i)} \rightarrow \mathbf{R}$ 可测,则 $f_{i}\left(X_{i, 1}, \ldots, X_{i, m(i)}\right)$ 独立.

习题2.1.6 从定义的方法直接得出两个独立随机变量各自可测函数独立.

如果 $X_{1}, \ldots, X_{n}$ 是独立的,那么 $X=X_{1}$ 和 $Y=X_{2} \cdots X_{n}$ 是独立的.

独立随机变量 $X_{1}, \ldots, X_{n}$ “和” $S_{m}=X_{1}+\cdots+X_{m}$ ,由定理2.1.10,那么 $S_{n}-S_{m}$ 独立于事件
$\left\{\max _{1 \leq k \leq m} S_{k}>x\right\}$
的示性函数.

3.2. 独立随机变量乘积期望

定理2.1.12 (多维独立随机变量函数的期望) 假设 $X$ 和 $Y$ 独立,并且有分布 $\mu$ 和 $\nu$ . 若 $\mathbf{R}^{2} \rightarrow \mathbf{R}$ 是可测函数, $\geq 0$ 或 $Y)|<\infty$ ,则
$Y)=\iint h(x, y) \mu(d x) \nu(d y)$
特别地,如果 $h (x, y) = f (x) g (y)$ ,其中 $\mathbf{R} \rightarrow \mathbf{R}$ 可测, $\geq 0$ 或 $E ∣ f (X) ∣$ 和 $E|g(Y)|<\infty$ 则
$\cdot E g(Y)$

习题2.1.14 计算独立随机变量乘积的分布函数

3.2.1. 独立的随机变量意味着不相关

推论2.1.13 独立的随机变量意味着不相关 如果 $X_{1}, \ldots, X_{n}$ 独立,且(a) 对所有 $i$ $X_{i} \geq 0$ ,或(b) 对所有 $E\left|X_{i}\right|<\infty$ ,则
$E\left(\prod_{i=1}^{n} X_{i}\right)=\prod_{i=1}^{n} E X_{i}$

举例2.1.14和习题2.1.4 说明不相关的随机变量不一定独立.

不相关 一个随机变量族 $X_{i} , i \in I$ 和 $X_{i}^{2}<\infty$ ,如果是不相关的 $E\left(X_{i} X_{j}\right)=E X_{i} E X_{j_{1}}$ 任意 $\neq j$ .

3.2.2. 独立随机变量和的分布

定理2.1.12的推论, 得到多个独立随机变量和的分布公式(定理2.1.15,定理2.1.16)

定理 2.1.15 (独立随机变量和的分市函数) 若 $X$ 和 $Y$ 独立, $\leq x)$ ,且 $\leq y)$ ,则
$\leq z)=\int F(z-y) d G(y)$
右侧积分称为 $F$ 和 $G$ 的卷积,定义为 $F * G (z)$ .

习题2.1.13 $X$ 和 $Y$ 不独立,同样也能满足上述公式的例子.

特例2.1.16 (独立随机变量和的分布) 假设 $X$ 有密度 $f, Y$ 分布函数为 $G$ ,两者相互独立. 则 $X + Y$ 有密度
$h(x)=\int f(x-y) d G(y)$
当 $Y$ 有密度 $g$ ,上式可写为 $h(x)=\int f(x-y) g(y) d y$

习题2.1.5推出两个独立随机变量求和为 0 的概率公式,且证得具有连续分布的独立随机变量相等的概率为 0.

习题2.1.10推出两个独立整数值随机变量求和为 $n$ 的概率公式.

两个标准的例子:多个独立伽马分布随机变量和的分布,多个独立高斯分布随机变量和的分布.

习题2.1.11和习题2.1.12 利用习题2.1.10证明两个独立Poission分布随机变量和的分布.\
利用习题2.1.10证明多个独立Binomial分布随机变量和的分布.

4. 独立随机变量的存在性

4.1. 有限个独立随机变量的构造

给定有限个随机变量的分布函数 $F_{i}, 1 \leq i \leq n$ ,容易构造带有分布函数 $P\left(X_{i} \leq x\right)=F_{i}(x)$ 的 $X_{1}, \ldots, X_{n}$ .

有限个独立随机变量的构造 令 $\Omega=\mathbf{R}^{n}, \mathcal{F}=\mathcal{R}^{n}, X_{i}\left(\omega_{1}, \ldots, \omega_{n}\right)=\omega_{i}\left(\omega \in \mathbf{R}^{n}\right.$ 的 $i$ 个坐标 $)$ ,令 $P$ 是 $\mathcal{R}^{n}$ 上的测度,有
$P\left(\left(a_{1}, b_{1}\right] \times \cdots \times\left(a_{n}, b_{n}\right]\right)=\left(F_{1}\left(b_{1}\right)-F_{1}\left(a_{1}\right)\right) \cdots\left(F_{n}\left(b_{n}\right)-F_{n}\left(a_{n}\right)\right)$
若 $\mu_{i}$ 是有分布函数 $F_{i}$ 的测度,则 $P=\mu_{1} \times \cdots \times \mu_{n}$ .

4.2. 无穷个独立随机变量的构造

为构造无穷多个带有分布函数的独立随机变量 $X_{1}, X_{2}, \ldots$ ,我们想把有限维的方法用到无穷维上
$\mathbf{R}^{\mathbf{N}}=\left\{\left(\omega_{1}, \omega_{2}, \ldots\right): \omega_{i} \in \mathbf{R}\right\}=\{\text { functions } \omega: \mathbf{N} \rightarrow \mathbf{R}\}$
其中, $\mathbf{N}=\{1,2, \ldots\} , \mathbf{N}$ 是自然数.

无穷个独立随机变量的构造 定义 $X_{i}(\omega)=\omega_{i}$ ,配备 $\mathbf{R}^{\mathbf{N}}$ 以乘积 $\sigma$ -代数 $\mathcal{R}^{\mathbf{N}}$ ,这由形式为 $\left\{\omega: \omega_{i} \in B_{i}, 1 \leq i \leq n\right\}$ 的有限维集合生成,其中, $B_{i} \in \mathcal{R}$ . 为把有限维 $P$ 存在性拓展到无穷维的 $\mathcal{R}^{\mathrm{N}}$ ,需要科尔莫戈罗夫延拓定理.

习题2.1.15 可以不用科尔莫戈罗夫延拓定理构造出抛硬币的无穷序列

其他可测空间的情形下,科尔莫戈罗夫延拓定理不成立,

无穷个取值于其他可测空间的独立随机变量的构造 有一类nice空间足以满足我们所有的结果,即科尔莫戈罗夫定理在这一空间的推广是自然的.

nice空间 $\mathcal{S})$ 被称为nice空间,如果存在从 $S$ 到 $\mathbf{R}$ 的 $1 - 1$ 映射 $\varphi$ 使得 $\varphi$ 和 $\varphi^{-1}$ 都可测.

这样的空间通常被称为标准的Borel空间,下一个结果表明,在应用中产生的大多数空间都是很好(nice)的.

定理2.1.22 (nice空间的判定) 如果 $S$ 是完备可分度量空间 $M$ 的Borel子集,且 $\mathcal{S}$ 是 $S$ 的Borel子集的集合,则 $\mathcal{S})$ 是 nice空间.

该分析的一个有趣的结果是,对于一个完全可分度量空间的Borel子集,连续体假设是正确的:即所有的集要么是有限的、可数无限的,要么是具有实数的基数.

这篇关于1.1. 大数定律-独立性的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

1.1. 大数定律-独立性

独立性