【数据结构C++】表达式求值（多位数）课程设计

本文主要是介绍【数据结构C++】表达式求值（多位数）课程设计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

📚博客主页：Zhui_Yi_
🔍：上期回顾：图

❤️感谢大家点赞👍🏻收藏⭐评论✍🏻，您的三连就是我持续更新的动力❤️
🎇追当今朝天骄，忆顾往昔豪杰。

前言

本期呢，给大家带来的课程设计，简单给大家说一哈要求：

问题描述

任 何 一 个 表 达 式 都 是 由 操 作 数 (operand)、 运 算 符 (operator)和 界 限 符
(delimiter)组 成 的 。 其 中 ， 操 作 数 可 以 是 常 量 ， 也 可 以 是 变 量 ； 运 算 符 可 以 是 算
术 运 算 符 、关 系 运 算 符 和 逻 位 算 符 ；界 限 符 是 左 、右 括 号 和 标 志 表 达 式 结 束 的 结 束 符。
在 本 课 程 设 计 中 ，仅 讨 论 简 单 算 术 表 达 式 的 求 值 问 题 ， 约 定 表 达 式 中 只 包 含 加 、减 、 乘 、 除 4 种运算， 所 有 的 运 算 对 象 均 为 简 单 变 量 ， 表 达 式 的 结 束 符 为 “ =”。
要 求以 字 符 序 列 的 形 式 从 终 端 输 入 语 法 正 确 、不 含 变 量 的 整 数 表 达 式 。 利 用 已 知 的 运 算 符 优 先 关 系 ， 实 现 对 算 术 表 达 式 的 求 值 。

基 本 要 求

这 是 一 个 利 用 栈 结 构 完 成 的 程 序 。为 了 实 现 运 算 符 优 先 算 法 ，需 使 用 两 个 工 作 栈 ，一 个 称 为 运 算 符 栈 (OPTR)， 用 来 寄 存 运 算 符 ； 另 一 个 称 为 操 作 数 栈 (OPND)， 用 来
寄 存 操 作 数 或 运 算 结 果 。 基 本 要 求 如 下 ： (1) 表 达 式 中 只 包 含 加 、 减 、 乘 、 除 4
种 运 算 ， 应 按 优 先 级 进 行 运 算 。
(2) 表 达 式 中 不 包 含 变 量 。
(3) 操 作 数 应 为 整 数
(4) 操 作 数 应 包 含 1 位 数 ， 2 位 数 ， 3 位 数 等 不 同 数 据 。
(5) 初 始 状态： 操作数栈(OPND)为空栈，表达式结束符“ =” 为 运 算 符 栈 (OPTR)的 栈 底 元 素 。

实 现 提 示

假 设 算 术 表 达 式 Expression 内 可 以 含 有 常 量 (0~9)和 二 元 运 算 符(+， -， *， /)。 实
现 以 下 操 作 ： (1) ReadExpre(E)： 对 以字符序列的形式输入语法正确的 中 缀表 达 式 并 构 造 表 达 式 E。
(2) EValuation()： 对 算 术 表 达 式 E 求 值 。 (3) Compare(c1,c2)： 比 较 运 算 符
优 先 级 。
(4) Operate(a,optr,b)：根 据 运 算 符 optr 进 行 操 作 数 a 和 b 的 运算 。
(5) 栈 的 相 关 操 作 （ 必 须 自 己 实 现 ， 不 可 使 用 现 成 的 模 板 类 ）。

一、摘要以及引言

摘要

本文介绍了一个利用链栈数据结构实现的简单中缀表达式求值程序。该程序能够接收用户输入的数学表达式，支持加减乘除四则运算及括号，以等号“=”作为输入结束标志，计算表达式的值并输出结果。本文详细阐述了程序的设计思路、核心算法及实现细节，旨在为初学者提供一个学习链栈应用和表达式求值原理的实践案例。

引言

在计算机科学领域，表达式求值是一项基本而重要的任务，广泛应用于编译器设计、计算器开发等多个场景。其中，中缀表达式是最自然的数学表达形式，但直接计算中缀表达式较为复杂。本文采用栈这一数据结构，设计并实现了一个程序，能够高效地将中缀表达式转换为后缀表达式（逆波兰表示法），进而计算其值。

二、系统设计

• 本系统主要由以下几个部分组成：
• 链栈结构：定义了两个链栈，OPTD用于存储操作数，OPTR用于存储运算符。
  表达式解析与计算：程序首先读取用户输入的中缀表达式，然后根据运算符优先级和括号规则，将表达式转换为便于计算的形式，并最终求得结果。
  用户交互：提供友好界面，用户输入表达式，以等号结束，程序显示计算结果，并询问是否继续进行新的计算。

三、关键算法与实现

1.运算符处理

• 运算符入栈规则：程序通过Precede函数判断新读入的运算符与栈顶运算符的优先级，优先级较低的运算符先出栈计算。
  括号处理：遇到左括号入栈，遇到右括号则弹出栈顶运算符直到遇到左括号，处理括号内表达式。
  等号处理：等号既是输入结束标志，也作为特殊运算符处理，确保表达式正确结束。

2.表达式求值流程

1. 初始化：初始化两个链栈。
2. 读取输入：逐字符读取用户输入的表达式。
3. 字符处理：对每个字符判断是否为运算符、数字或结束符号，进行相应处理。
4. 运算符优先级判定与操作数计算：使用栈结构辅助计算，遵循运算符优先级规则。
5. 输出结果：计算完成后，输出表达式的计算结果。

四、程序实现

本程序使用C++语言实现，主要采用了结构体定义链栈，通过自定义的链栈操作函数实现了数据的入栈、出栈等操作。calculate函数为核心，负责解析和计算表达式。通过一系列条件判断和循环结构，实现了对中缀表达式的有效处理。此外，程序还包含用户交互环节，提高了用户体验。

五、具体代码

1.定义结构以及初始化

// 链栈节点结构
struct Node {double data;Node* next;
};// 链栈结构
struct LinkStack {Node* top;int size;
};// 初始化链栈
LinkStack* InitLinkStack() {LinkStack* stack = new LinkStack;stack->top = nullptr;stack->size = 0;return stack;
}

2.简单的链栈操作

判空

bool IsEmpty(LinkStack* stack) {return stack->top == nullptr;
}

入栈

// 入栈操作
void Push(LinkStack* stack, double value) {Node* node = new Node;node->data = value;node->next = stack->top;stack->top = node;stack->size++;
}

出栈

double Pop(LinkStack* stack) {if (IsEmpty(stack)) {throw runtime_error("栈是空的！");}double value = stack->top->data;Node* temp = stack->top;stack->top = stack->top->next;delete temp;stack->size--;return value;
}

取栈顶元素

// 获取栈顶元素
double GetTop(LinkStack* stack) {if (IsEmpty(stack)) {throw runtime_error("栈是空的！");}return stack->top->data;
}

判断运算符是否有效

运算符分为+、-、*、/、=，即：

bool In(char c) {if (c == '(' || c == ')' || c == '+' || c == '-' || c == '*' || c == '/' || c == '=')return true;return false;
}

将运算符转换

int intdata(char c) {switch (c) {case '+': return 0;case '-': return 1;case '*': return 2;case '/': return 3;case '(': return 4;case ')': return 5;case '=': return 6; default: break;}
}

判断运算符优先级

根据这张图片进行建立二维数组。

char Precede(char c1, char c2) {int a, b;char table[7][7] = {'>','>','<','<','<','>','>','>','>','<','<','<','>','>','>','>','>','>','<','>','>','>','>','>','>','<','>','>','<','<','<','<','<','=','0','>','>','>','>','0','>','>','<','<','<','<','<','0','=',};a = intdata(c1); b = intdata(c2);return table[a][b];
}

进行运算

double operate(double a, char c, double b) {if (c == '+') return (a + b);else if (c == '-') return (a - b);else if (c == '*') return (a * b);else if (c == '/') {if (b == 0) return (flag = 1);else return (a / b);}
}

进行运算

double calculate() {char ch, tempc;double x, y, temp, count = 0;Push(OPTR, '='); cin >> ch;while (ch != '=' || GetTop(OPTR) != '=') { if (!In(ch)) {if (count != 0) {temp = GetTop(OPTD); Pop(OPTD);temp = (double)(temp * 10 + ch - '0');Push(OPTD, temp);cin >> ch;}else {temp = (double)(ch - '0');Push(OPTD, temp);count++;cin >> ch;}}else {count = 0;switch (Precede(GetTop(OPTR), ch)) {case '<':Push(OPTR, ch);cin >> ch;break;case '>':tempc = GetTop(OPTR); Pop(OPTR);y = GetTop(OPTD); Pop(OPTD);x = GetTop(OPTD); Pop(OPTD);Push(OPTD, operate(x, tempc, y));break;case '=':tempc = GetTop(OPTR); Pop(OPTR);cin >> ch;break;default:break;}}}return GetTop(OPTD);
}

完整代码

#include <iostream>
#include <string>using namespace std;// 链栈节点结构
struct Node {double data;Node* next;
};// 链栈结构
struct LinkStack {Node* top;int size;
};// 初始化链栈
LinkStack* InitLinkStack() {LinkStack* stack = new LinkStack;stack->top = nullptr;stack->size = 0;return stack;
}// 判断栈是否为空
bool IsEmpty(LinkStack* stack) {return stack->top == nullptr;
}// 入栈操作
void Push(LinkStack* stack, double value) {Node* node = new Node;node->data = value;node->next = stack->top;stack->top = node;stack->size++;
}// 出栈操作
double Pop(LinkStack* stack) {if (IsEmpty(stack)) {throw runtime_error("栈是空的！");}double value = stack->top->data;Node* temp = stack->top;stack->top = stack->top->next;delete temp;stack->size--;return value;
}// 获取栈顶元素
double GetTop(LinkStack* stack) {if (IsEmpty(stack)) {throw runtime_error("栈是空的！");}return stack->top->data;
}// 全局链栈
LinkStack* OPTD = InitLinkStack();
LinkStack* OPTR = InitLinkStack();
int flag = 0;// 判断字符是否为运算符
bool In(char c) {if (c == '(' || c == ')' || c == '+' || c == '-' || c == '*' || c == '/' || c == '=')return true;return false;
}// 将运算符转换为序号
int intdata(char c) {switch (c) {case '+': return 0;case '-': return 1;case '*': return 2;case '/': return 3;case '(': return 4;case ')': return 5;case '=': return 6; // 修改这里，添加'='的序号default: break;}
}// 判定运算符优先级
char Precede(char c1, char c2) {int a, b;char table[7][7] = {'>','>','<','<','<','>','>','>','>','<','<','<','>','>','>','>','>','>','<','>','>','>','>','>','>','<','>','>','<','<','<','<','<','=','0','>','>','>','>','0','>','>','<','<','<','<','<','0','=',};a = intdata(c1); b = intdata(c2);return table[a][b];
}// 执行运算
double operate(double a, char c, double b) {if (c == '+') return (a + b);else if (c == '-') return (a - b);else if (c == '*') return (a * b);else if (c == '/') {if (b == 0) return (flag = 1);else return (a / b);}
}// 表达式求值
double calculate() {char ch, tempc;double x, y, temp, count = 0;Push(OPTR, '='); cin >> ch;while (ch != '=' || GetTop(OPTR) != '=') { if (!In(ch)) {if (count != 0) {temp = GetTop(OPTD); Pop(OPTD);temp = (double)(temp * 10 + ch - '0');Push(OPTD, temp);cin >> ch;}else {temp = (double)(ch - '0');Push(OPTD, temp);count++;cin >> ch;}}else {count = 0;switch (Precede(GetTop(OPTR), ch)) {case '<':Push(OPTR, ch);cin >> ch;break;case '>':tempc = GetTop(OPTR); Pop(OPTR);y = GetTop(OPTD); Pop(OPTD);x = GetTop(OPTD); Pop(OPTD);Push(OPTD, operate(x, tempc, y));break;case '=':tempc = GetTop(OPTR); Pop(OPTR);cin >> ch;break;default:break;}}}return GetTop(OPTD);
}// 菜单函数
void menu() {puts("\n=========================\n");puts("       表达式求值");puts("\n=========================\n");
}// 主函数
int main() {menu();double answer, trueValue = 1;while (trueValue) {cout << "\n请输入表达式，以等号（=）结束："; answer = calculate();if (flag == 1) {cout << "分母不能为0哦!" << endl;flag = 0;}elsecout << "表达式的值为：" << answer << endl;cout << "按0可结束程序，继续请按1：";cin >> trueValue;}return 0;
}

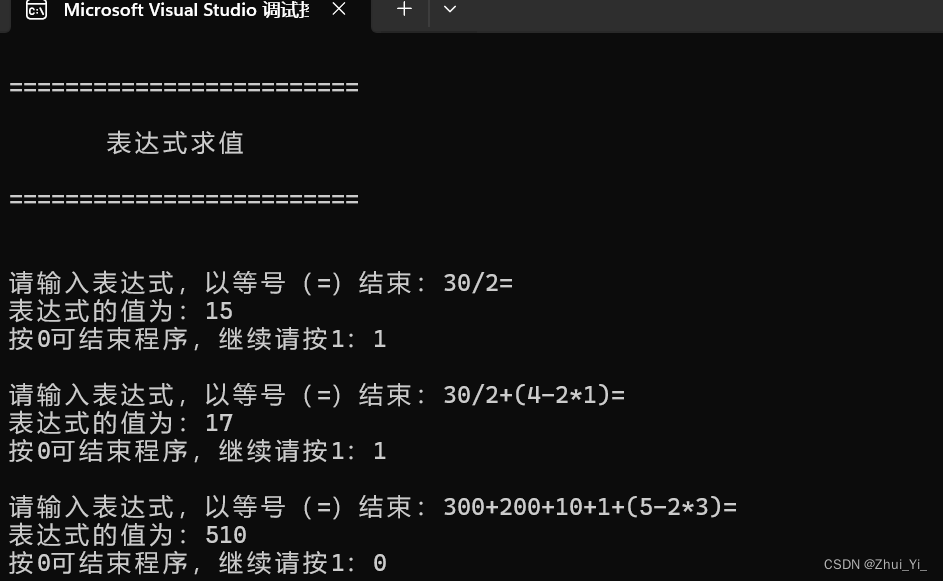
总结

本文通过设计链栈数据结构和实现相应的算法，成功开发了一个能够处理中缀表达式的程序。该程序不仅能够正确计算表达式的值，还具备良好的用户交互体验，适合教学和初步编程实践。未来的工作可以考虑扩展程序功能，支持更多类型的运算符和更复杂的表达式结构。

切记切记，我给出代码缺少对括号匹配的信息，但代码是能直接运行的，需要你们自己写出来。

这篇关于【数据结构C++】表达式求值（多位数）课程设计的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---