线性结构——尺取法

2024-06-17 21:32

文章标签 结构线性取法

本文主要是介绍线性结构——尺取法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【概述】

尺取法，顾名思义，就是像尺子一样一段一段的取，简单来说，尺取法就是返回推进区间开头和结尾，求满足条件的最小区间的方法。

一般在以下两种情况使用尺取法：

给定一个有序递增数组，在数组中找到满足条件的区间
给定长度为 n 的数列以及整数 s，求出不小于 s 的连续子序列的长度的最小值，即最优连续子序列问题

【基本思路】

尺取法本质上也是一种模拟，常用于解决寻找区间和问题。

假设有一问题：给定一个序列{5,1,3,5,10,7,4,9,2,8}，在这些数中找一个区间，使得区间中每个元素的和大于或等于给定的值 S=15，求最短的子序列长度。

对于上述问题，不用尺取法的话，肯定就会开双重循环，枚举区间起点和终点，然后每一次都求一次和，再和给定的数作比较。但这样时间复杂度达到 O(n^2)，而使用尺取法，时间复杂度会降到 O(n)

尺取法的思路与双重循环枚举的思路类似，都是寻找一个区间的起点和终点，尺取法的基本思路是:

定义两个指针，将两个指针的看做一个区间范围，且他们最初都指向这一组数中的第一个
如果这个指针区间范围内的元素之和小于给定的数，就把右指针向右移，直到区间和大于等于给定的值为止
然后把左指针向右移，直到区间和等于给定的值为止
保存方案，更新最优方案，继续操作
假如左指针指向这些数的第一个，并且右指针指向这组数的最后一个，这种情况下的子区间元素之和仍然小于给定的数的话，那么就输出 -1，表示不可能。

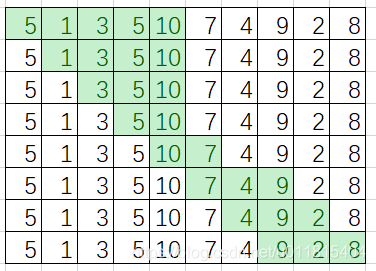
如下图，是使用尺取法每一次得到的答案，可以得到最短长度为 2

【模版】

void solve(){int L=1,R=1;//两个指针int sum=0;//区间和int now=0;//当前方案int minn=INF;while(R<=N){while(sum<S&&R<=N){//R总指向当前满足要求区间的下一个，此处R可能>N sum+=a[R];//累加器加上右指针指向的元素++R;//右指针向右移++now;}while(sum>=S){//L总指向当前区间的最左边，左闭右开 sum-=a[L];//累加器减去左指针指向的元素的值++L;//左指针右移--now;}minn=min(minn,now+1);//更新最优方案}
}