本文主要是介绍C语言最终文章-二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 前言
- 二叉树的性质
- 二叉树的存储方式
- 顺序存储
- 堆及其应用
- TopK问题
- 堆排序
- 链式存储
- 二叉树的练习
- 1.二叉树查找值为x的节点
- 2.判断是否为完全二叉树
- LC226.翻转二叉树
- [LC572. 另一棵树的子树](https://leetcode.cn/problems/subtree-of-another-tree/description/)
- 两道选择题
- 结言
前言
- 这篇文章大概就是我C语言学习的最后一篇文章了。
本篇文章主要内容:
- 二叉树的几个性质,堆、堆排序和用堆实现TopK问题。
- 向上建堆和向下建堆
- 二叉树的练习
二叉树原图:

二叉树的性质
开始讲二叉树时,我们先来学一下二叉树的重要性质。
1.对于任意二叉树: n 0 = n 2 + 1 n0 = n2+1 n0=n2+1 (其中 n0代表度为0的个数,n2代表度为2的节点个数)
2. N − 1 = n 0 ∗ 0 + n 1 ∗ 1 + n 2 ∗ 2 + . . . . N-1 =n0*0+n1*1+n2*2+.... N−1=n0∗0+n1∗1+n2∗2+.... (N-1代表边的个数)
3. 对于满二叉树来说,二叉树节点个数 = 2 h − 1 2^h-1 2h−1 (h为二叉树的高度)
先来看第一条, n 0 = = n 2 + 1 ? n0 ==n2+1? n0==n2+1?
来让我们想一想二叉树是如何构建的呢?
首先我们要明白一件事: 首先我们要明白一件事: 首先我们要明白一件事: 度为1的是有度为0的节点增加一个分支得来的,度为2的是由度为1的节点增加一个分支得来的。
一开始我们只有一个根节点,那么我们的 n 0 = 1 n0=1 n0=1,当我们增加一个度为1的
节点时,那么此时我们的 n 0 还是 = 0 , n 1 = 1 n0还是 = 0,n1=1 n0还是=0,n1=1,当我们增加一个度为2的时候
n 0 − > 2 , n 1 − > 0 , n 2 − > 1 n0->2,n1->0,n2->1 n0−>2,n1−>0,n2−>1
过程如下图:
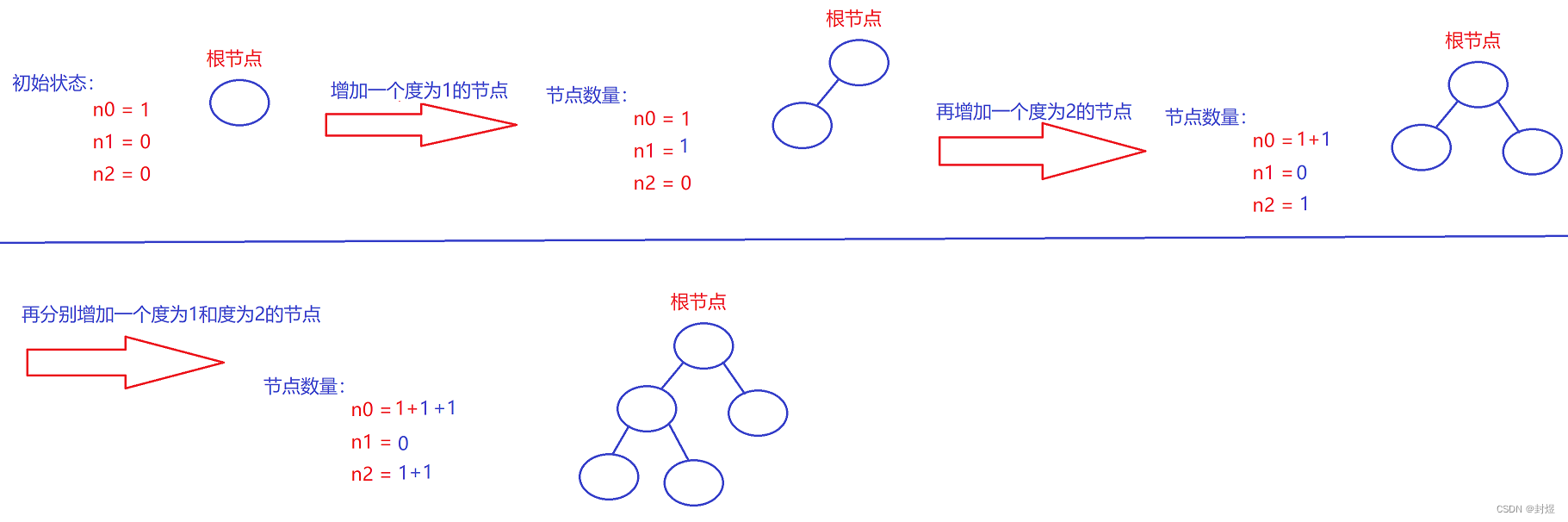
那我们不难发现,我们的 n 0 = n 2 + 1 n0=n2+1 n0=n2+1 这个条件始终成立,只要我们增加一个度为2的节点,那么n0肯定会增加一个。
再来看第二条,对与一棵树而言,子数肯定也是一棵树,两个兄弟节点之间也
不会有连线。那么 N 个节点就可以形成 N-1 条边。而 n0 有有0条边,n1有1条边…,那么总的边数 N-1 就可以得出来第二条的公式。
第三条
- 对于一个满二叉树来说
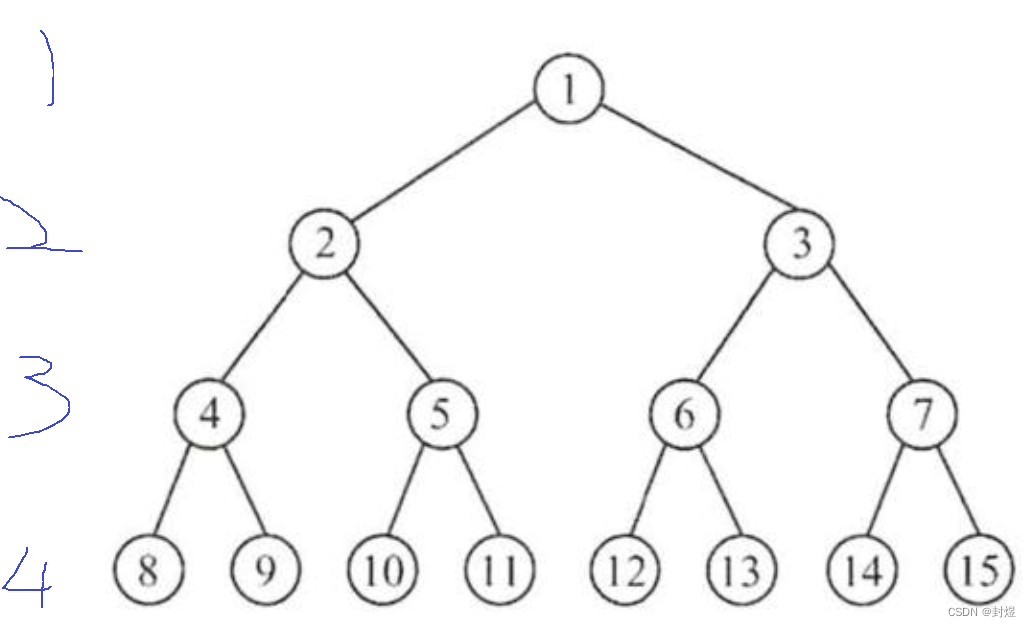
- 第一层节点个数: 2 0 2^0 20
- 第二层节点个数: 2 1 2^1 21
- 第三层节点个数: 2 2 2^2 22
- 第四层节点个数: 2 3 2^3 23
那么如果一个h层的满二叉树它的节点总数 T(N) = 2 0 + 2 1 + 2 2 + . . . + 2 h − 1 2^0+2^1+2^2+...+2^{h-1} 20+21+22+...+2h−1
所以 T ( N ) = 2 h − 1 T(N) = 2^{h}-1 T(N)=2h−1
二叉树的存储方式
顺序存储
顺序存储本质上就是用数组存。这里我们理解一下完全二叉树和满二叉树
- 满二叉树:各层的节点都是满的状态-就如上面那个图一样如上图
- 完全二叉树:前 h-1层都是满的,第h层从右向左连续去掉节点。这就相当于,在最后一层它的节点必须是连续的。
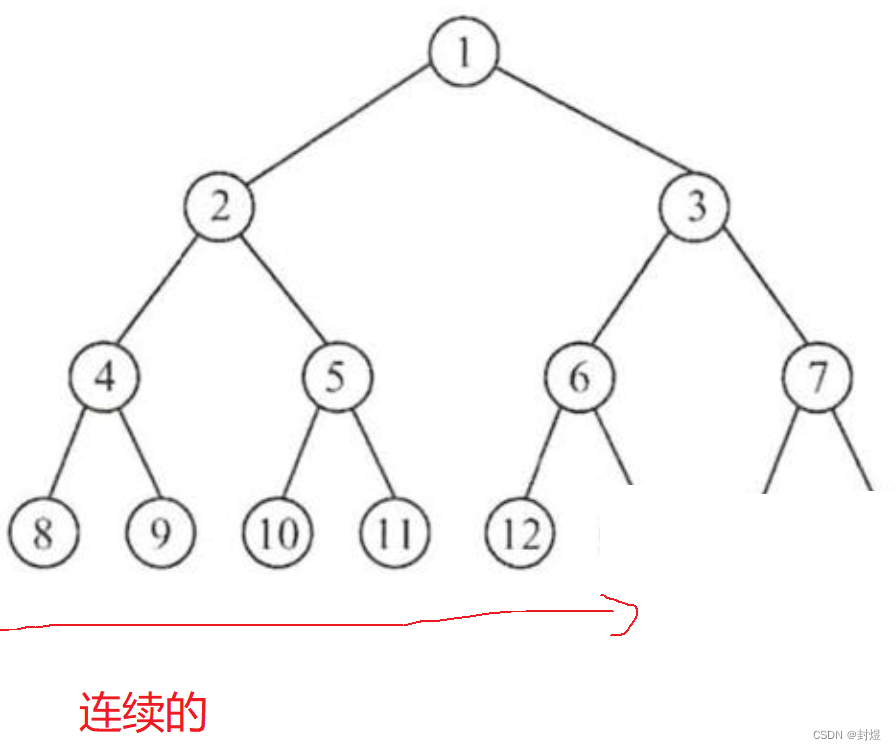
理解完这两个概念之后,如果我们把这些二叉树的节点都放入数组中会怎么样呢? 如图:
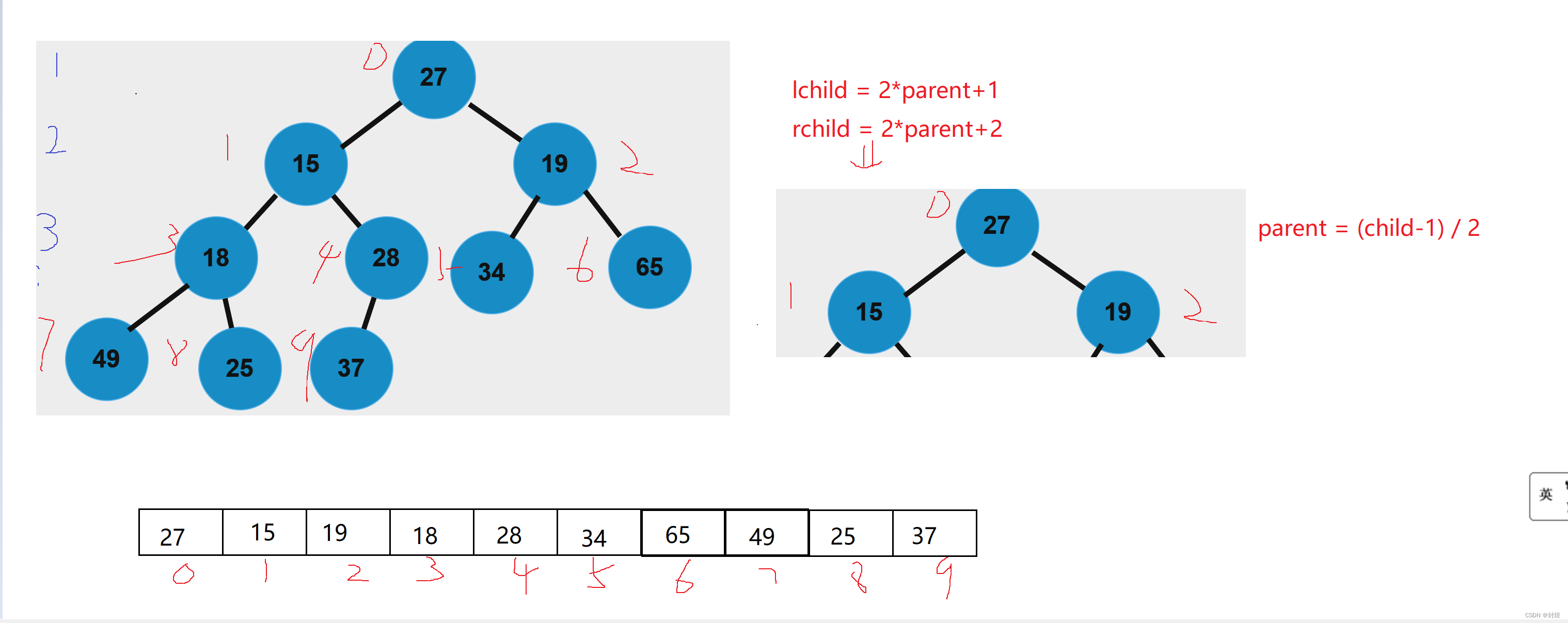
当我们把树的节点都放入数组中后,我们发现双亲节点和它的左孩子和右孩子之间存在这么一个关系。 - l c h i l d i = 2 ∗ p a r e n t i + 1 , r c h i l d i = 2 ∗ p a r e n t i + 2 lchild_i = 2*parent_i+1,rchild_i = 2*parent_i+2 lchildi=2∗parenti+1,rchildi=2∗parenti+2
- p a r e n t i = ( ( l , r ) c h i l d i − 1 ) / 2 parent_{i} = ((l,r)child_i-1)/2 parenti=((l,r)childi−1)/2
注意: 这个规则只对完全二叉树和满二叉树使用,当然其他的二叉树我们也可以这么存储,只不过途中我们要把位置空出来,这样比较浪费空间,所以我们会使用下面的链式存储。
堆及其应用
当我们对顺序存储有了以上的了解后,我们就可以来实现堆了。注意这里的堆跟操作系统的堆可不一样,我们这里只是一个数据结构。
堆的操作:
- 入堆
- 出堆顶元素
- 取堆顶元素
- 判空
堆可以用来做什么呢?
比如:排出中国最有钱的前10个人,堆排序等等。
这里先介绍两个概念:
- 大堆:堆顶元素比其他元素大
- 小堆:堆顶元素比其他元素小
为什么要有这两个堆呢?
同时注意:大堆和小堆并不意味着有序。
如下图:大堆和小堆,只能说明堆顶元素,一定比其他元素大,由于二叉树左子树和右子树是两个子树。子树和树具有相同的性质
- 对于大堆而言: 左子树也是大堆,右子树也是大堆,那么左子树的左子树也是大堆…
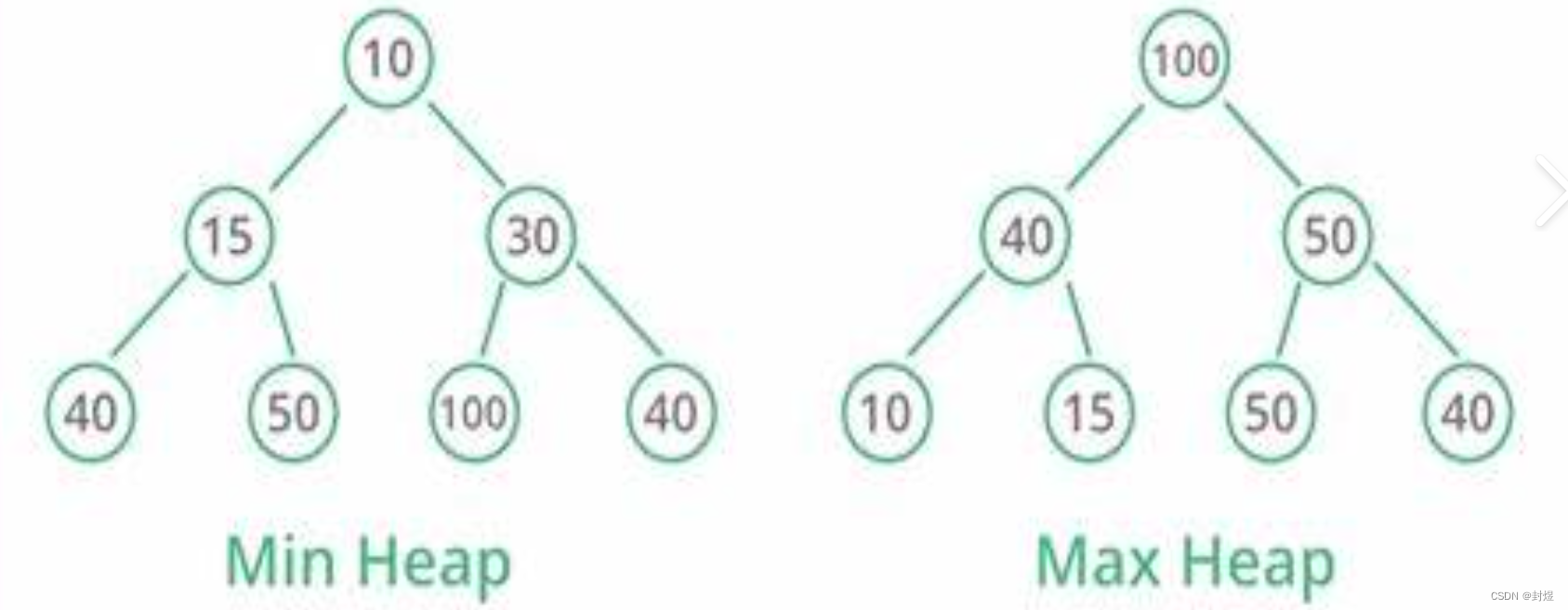
如果你要排升序的话,利用堆排大堆还是小堆呢呢?
如果排小堆,那么每次堆顶就是我们的最小元素,但是然后怎么排呢?这样剩
下的元素就不一定是小堆了。所以当我们排升序的时候我们排大堆,直接把堆顶元素与最后一个位置的元素交换,注意这时我们下面的子树并没有受影响,所以我们直接再排一次大堆就可以了。然后不断的排,数组就有序了。
下面我们都以建大堆为例:
先来说入堆:
入堆的话,我们需要用到向上调整算法。
算法演示如下:
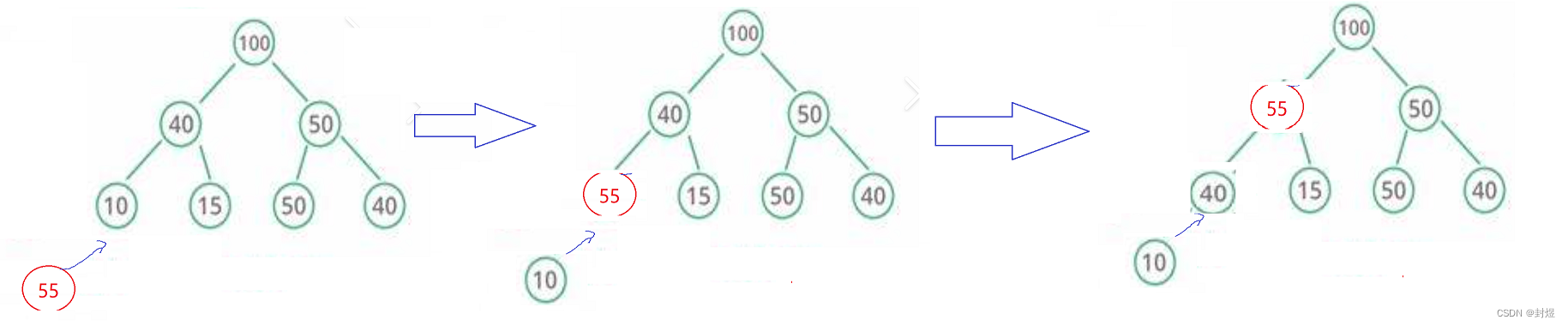
当我们插入一个新元素后,不断地去找双亲节点判断大小,如果比双亲的值大
那么就交换,否则就不交换。
代码:
void ADjustUp(HpDataType* a, int n)
{int child = n - 1;int parent = (n - 1 - 1) / 2;while (parent >= 0){if (a[child] > a[parent]) //大的往上调{swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}
void HpPush(Hp* hp, HpDataType x)
{assert(hp);check_capacity(hp); //检查容量hp->a[hp->size] = x;hp->size++;ADjustUp(hp->a,hp->size); // 开区间
}
出堆顶元素:
这里我们就要用到 向下调整算法:,由于我们必须保证树是一个大堆,所以每次把堆顶元素Pop调后,要保证树还是一个大堆。
这里我们直接把堆顶 a[0] 与 最后一个元素交换。我们本质上还是数组。
然后再用一次向下调整算法即可。
向下调整算法过程如图:

代码:
void AdjustDown(HpDataType* a, int begin, int end)
{int parent = begin;int child = 2 * parent + 1;while (child < end){if (child + 1 < end && a[child] > a[child + 1]){child += 1;}if (a[parent] > a[child]){swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;}elsebreak;}
}
//出堆
void HpPop(Hp* hp)
{assert(hp && hp->size > 0);swap(&hp->a[0],&hp->a[hp->size-1]);//此时这个位置就不能才排了hp->size--;AdjustDown(hp->a,0,hp->size); }
堆的总代码:
typedef int HpDataType;
typedef struct Heap
{HpDataType* a;int size;int capacity;
}Hp;//初始化堆
void HpInit(Hp* hp);
//销毁堆
void HpDestory(Hp* hp);
//入堆
void HpPush(Hp* hp, HpDataType x);
//出堆
void HpPop(Hp* hp);
//判空
bool HpEmpty(Hp* hp);
//堆顶元素
HpDataType HpTop(Hp* hp);
//向下
void AdjustDown(HpDataType* a, int begin, int end);void swap(HpDataType* e1, HpDataType* e2);void swap(HpDataType* e1, HpDataType* e2)
{HpDataType tmp = *e1;*e1 = *e2;*e2 = tmp;
}//初始化堆
void HpInit(Hp* hp)
{hp->size = 0;hp->capacity = 4;hp->a = (HpDataType*)malloc(sizeof(HpDataType) * (hp->capacity));if (hp->a == NULL){perror("malloc fail!\n");exit(-1);}
}
//销毁堆
void HpDestory(Hp* hp)
{hp->size = hp->capacity = 0;free(hp->a);
}
void check_capacity(Hp* hp)
{if (hp->capacity == hp->size){HpDataType* ptr = (HpDataType*)realloc(hp->a, sizeof(HpDataType) * (hp->capacity * 2));if (ptr == NULL){printf("realloc fail!\n");exit(-1);}hp->capacity *= 2;hp->a = ptr;}
}//排倒序 - 建大堆
void ADjustUp(HpDataType* a, int n)
{int child = n - 1;int parent = (n - 1 - 1) / 2;while (parent >= 0){if (a[child] > a[parent]) //大的往上调{swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}
//入堆
void HpPush(Hp* hp, HpDataType x)
{assert(hp);check_capacity(hp);hp->a[hp->size] = x;hp->size++;ADjustUp(hp->a,hp->size); // 开区间
}
//堆顶元素
HpDataType HpTop(Hp* hp)
{assert(hp && hp->size > 0);return hp->a[0];
}
//建大堆
void AdjustDown(HpDataType* a, int begin, int end)
{int parent = begin;int child = 2 * parent + 1;while (child < end){if (child + 1 < end && a[child] > a[child + 1]){child += 1;}if (a[parent] > a[child]){swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;}elsebreak;}
}
//出堆
void HpPop(Hp* hp)
{assert(hp && hp->size > 0);swap(&hp->a[0],&hp->a[hp->size-1]);//此时这个位置就不能才排了hp->size--;AdjustDown(hp->a,0,hp->size); }
//判空
bool HpEmpty(Hp* hp)
{return hp->size == 0;
}
TopK问题
现在有一个问题
- 你只有1KB的空间,如何把在4G的文件(假设都是整数)中找出前K(K > 0)大的数字
既然我们学的是堆,肯定使用堆来解决,如果没有空间限制的话,我们可以把数据都读到内存中,然后排K次大堆即可。可关键我们只有1KB(1024byte)的空间,那如何做呢?

排成小堆后,堆顶元素就是最小值,每次读入一个比堆顶大的数据,读到最后就是前K个最大的数据了。
代码实现:
#define N 100000 //这里以 10万个数据为例子。
//创建数据
void CreatData()
{FILE* fin = fopen("data.txt", "w");if (fin == NULL){perror("fopen fail!\n");exit(-1);}int i = 0;srand(time(0));for (i = 0; i < N; i++){int x = (rand() + i) % 10000;fprintf(fin,"%d\n", x);}fclose(fin);
}//要求:只给你1KB空间,排出4G个整数的前K个最大值
void TopK()
{FILE* fout = fopen("data.txt","r");if (fout == NULL){perror("fopen fail!\n");exit(-1);}int k;printf("请输入k>: ");scanf("%d", &k);int i = 0;int* KminArr = (int*)malloc(sizeof(int) * k);//读取K个数建最小堆for (i = 0; i < k; i++){fscanf(fout,"%d",&KminArr[i]);}int x = 0;while (fscanf(fout, "%d", &x) > 0){if (x > KminArr[0]){KminArr[0] = x;AdjustDown(KminArr,0,k);}}HeapSort(KminArr,k);//前k个最大值printf("前%d个最大值为:", k);for (i = 0; i < k; i++){printf("%d ", KminArr[i]);}printf("\n");
}
堆排序
当我们了解了向上和向下两种算法的时候,我们就可以来实现啊堆排序了。
如果给你这样一个数组,如何排序呢?

思路:
建大堆,不断交换堆顶和数组最后一个位置的元素,然后再对剩下的数字进行向下调整算法。直到数组有序为止。
关键就是,我们如何去建大堆呢,前面我们讲堆的时候,那数组经过向上调整算法之后,本来就是一个大堆(ps:建大堆的前提就是源数据也是大堆)。那我们拿到一个随机的数组之后如何建大堆呢?
- 以最后一个非叶子节点为开始,不断向下调整,直到达到堆顶,此时即为大堆。
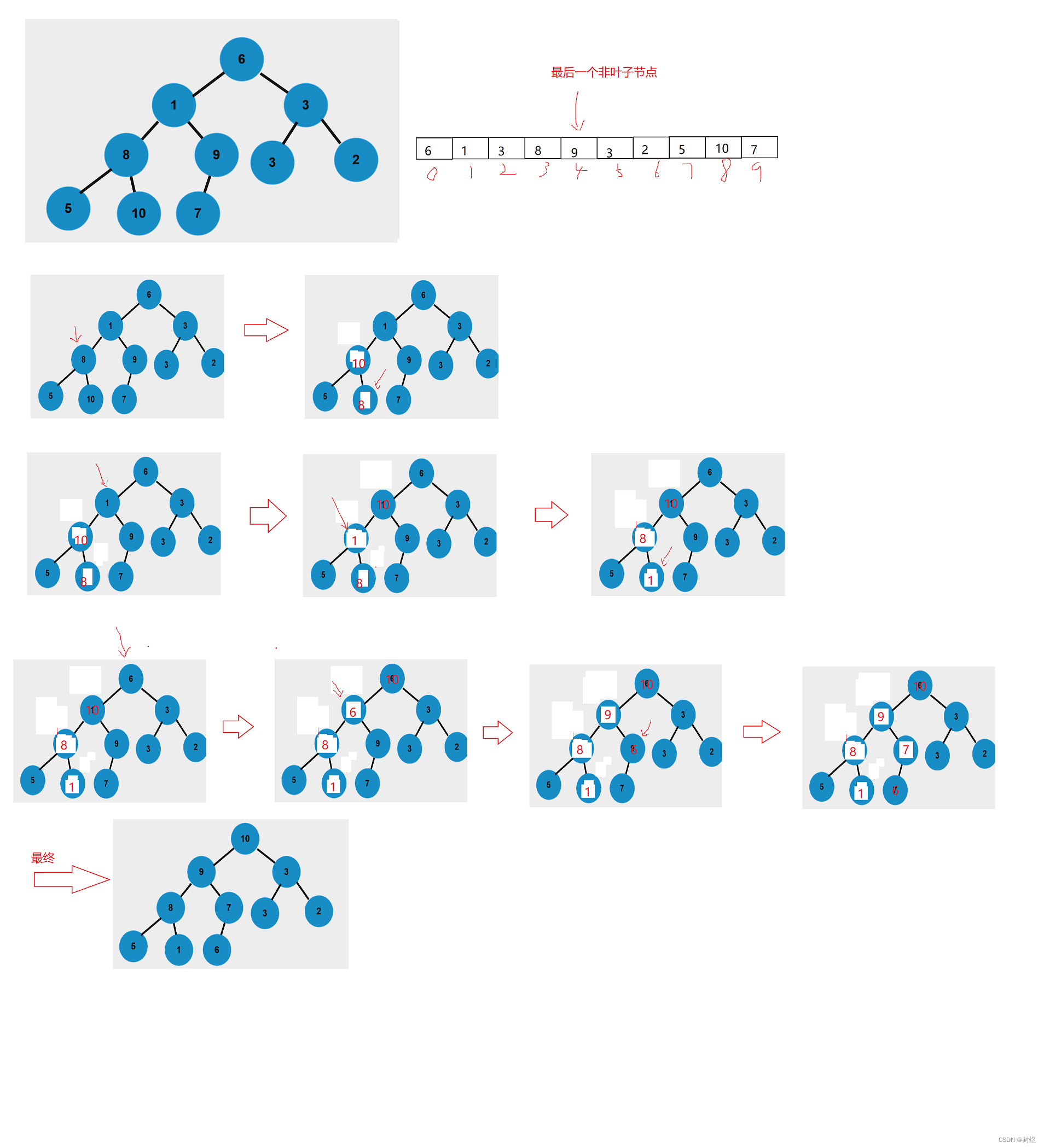
建完大堆之后,不断交换堆顶和数组最后一个位置的元素,然后再对剩下的数字进行向下调整算法。
总代码:
void HeapSort(int* a, int n)
{int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a,i,n);}int end = n - 1;while (end > 0){swap(&a[end],&a[0]);AdjustDown(a,0,end);end--;}
}void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}
void TestHeapSort()
{int a[] = { 6,1,3,8,9,3,2,5,10,7 };int sz = sizeof(a) / sizeof(a[0]);HeapSort(a,sz);PrintArray(a,sz);
}
那么堆排序的时间复杂度是多少呢?
我们先来看一下建堆的复杂度:
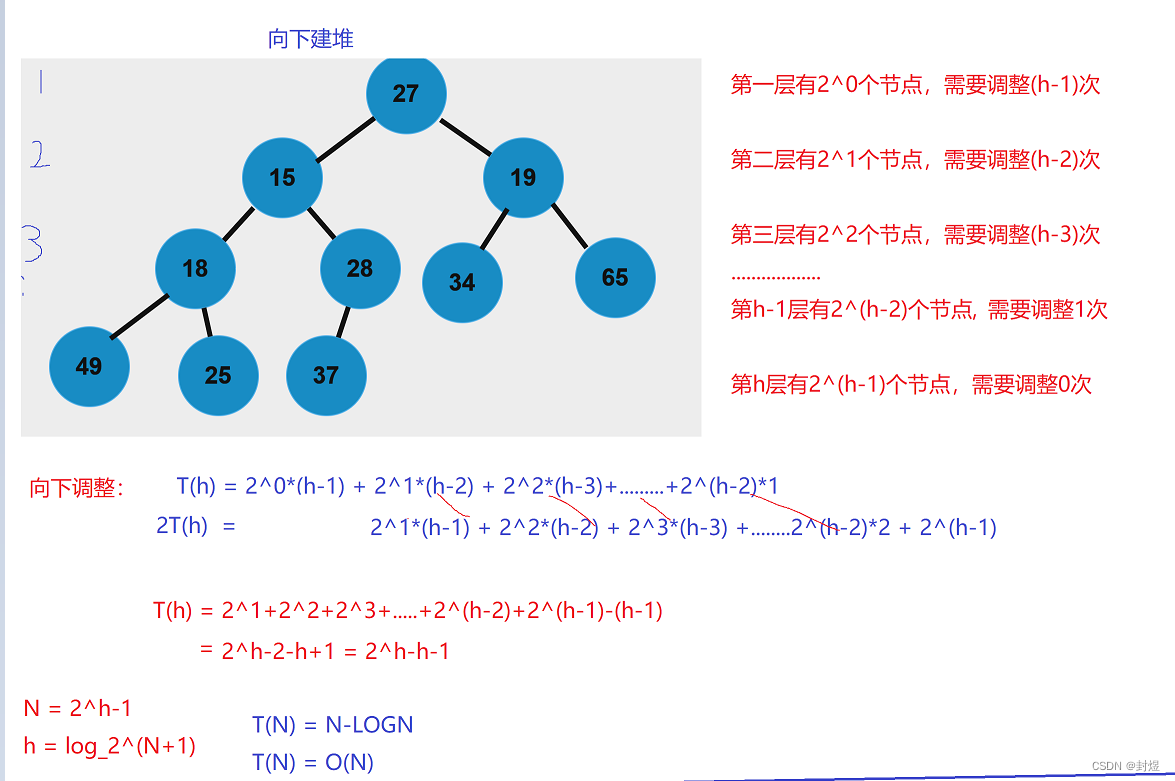
建堆是 O(N),下面交换以及排大堆是 N*LOGN,按照大O渐进表示法,我们堆排序的时间复杂度为: O ( N ∗ L O G N ) O(N*LOGN) O(N∗LOGN)。
再来看一下向上调整算法,建堆的复杂度:

这也是为什么我们不用向上调整算法的原因。
链式存储
先来看一下链式二叉树如何定义。
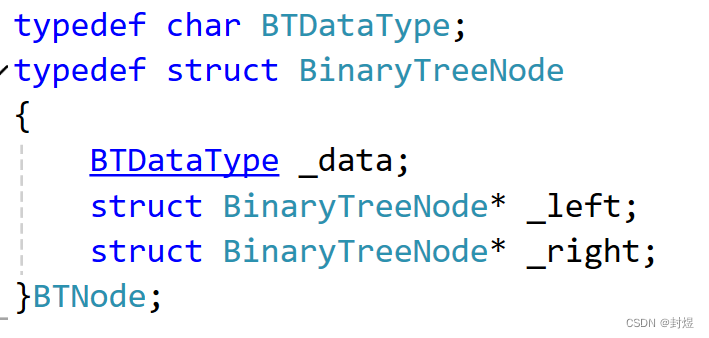
每一个节点我们都有数据和左孩子和右孩子。直接看遍历方式
链式二叉树有那么四种遍历方式,他们的访问方式为:
- 前序遍历: 根 − > 左子树 − > 右子树 根->左子树->右子树 根−>左子树−>右子树
- 中序遍历: 左子树 − > 根 − > 右子树 左子树->根->右子树 左子树−>根−>右子树
- 后序遍历: 左子树 − > 右子树 − > 根 左子树->右子树->根 左子树−>右子树−>根
很明显,这三种遍历方式很适合用递归来解决。
再来看一下层序遍历 (以上面大堆结果为例):
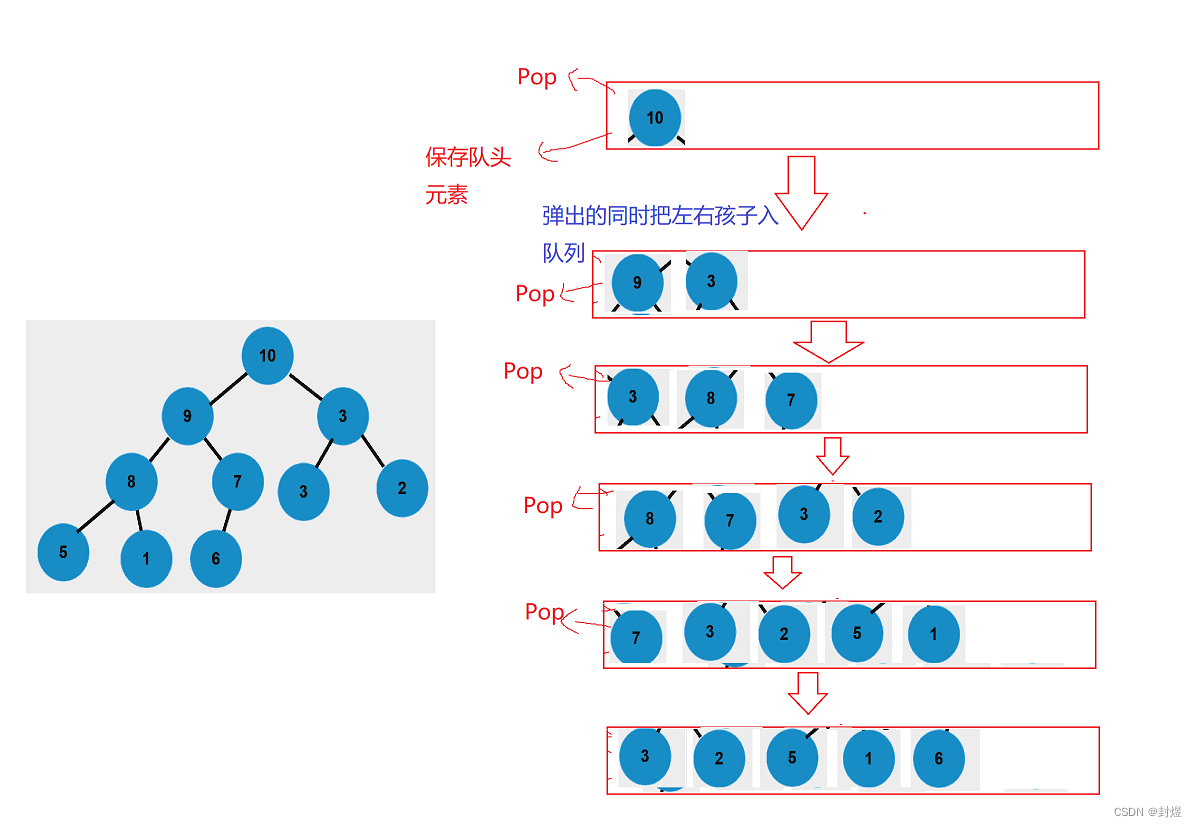
然后再挨个把队列的元素,Pop完就可以了,由于我们现在队列的元素是树的节点,所以最后队列里面全是 N U L L NULL NULL 。
- 层序遍历的结果:就是按照层次把树中的元素打印出来。这里我们打印的就为 10 − > 9 − > 3 − > 8 − > 7 − > 3 − > 2 − > 5 − > 1 − > 6 10->9->3->8->7->3->2->5->1->6 10−>9−>3−>8−>7−>3−>2−>5−>1−>6
代码实现:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL)return;printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL)return;BinaryTreePrevOrder(root->_left);printf("%c ", root->_data);BinaryTreePrevOrder(root->_right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL)return;BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);printf("%c ", root->_data);
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q,root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->_data);if (front->_left){QueuePush(&q,front->_left);}if (front->_right){QueuePush(&q, front->_right);}}QueueDestroy(&q);}
二叉树的练习
1.二叉树查找值为x的节点
思路:
- 如果此时我们这个节点的值 == 我们要找的值,直接返回即可。
- 如果不等于取左右子树去找
- 返回其中一个答案。
代码:
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* left = BinaryTreeFind(root->_left,x);BTNode* right = BinaryTreeFind(root->_right,x);return left == NULL ? right : left;
}
2.判断是否为完全二叉树
思路:
非完全二叉树我们测序遍历的时候跟完全二叉树有什么区别呢?
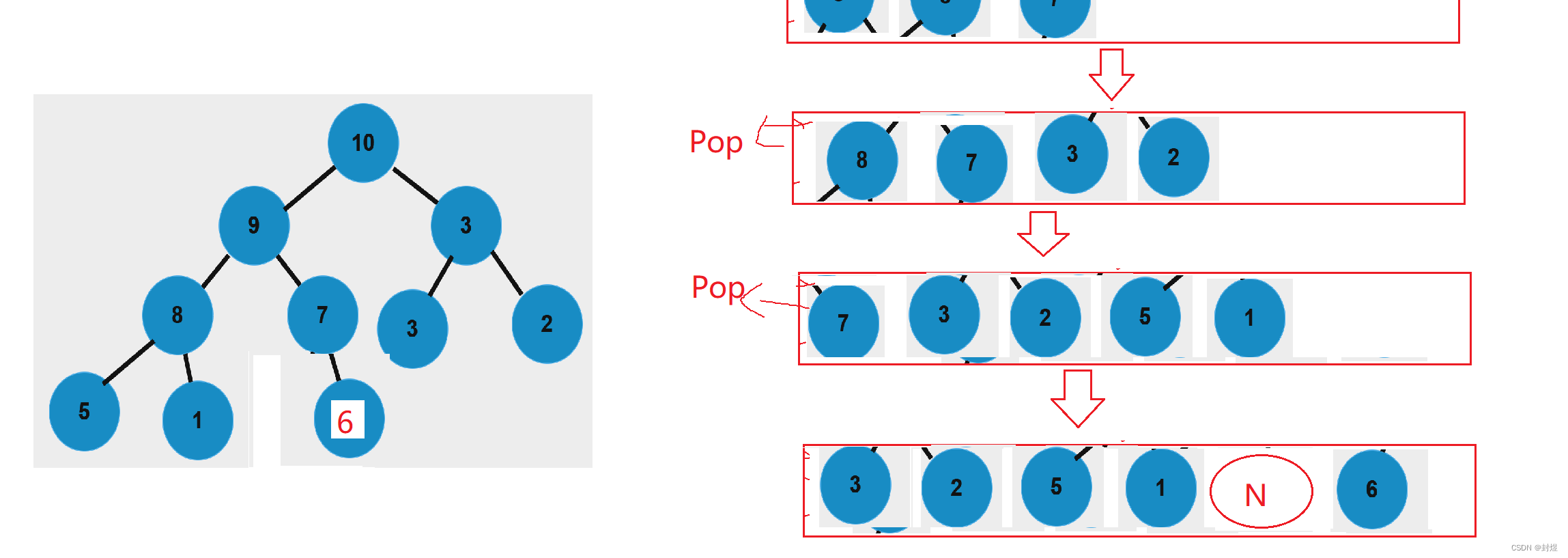
那就是我们会入空值进去,所以当我们取队头元素去到空值的时候,我们要判断如果队列中出现了非空的值,那就说明这时一个非完全二叉树。
代码:
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q,front->_left);QueuePush(&q,front->_right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);if (front != NULL)return false;QueuePop(&q);}QueueDestroy(&q);return true;
}
LC226.翻转二叉树
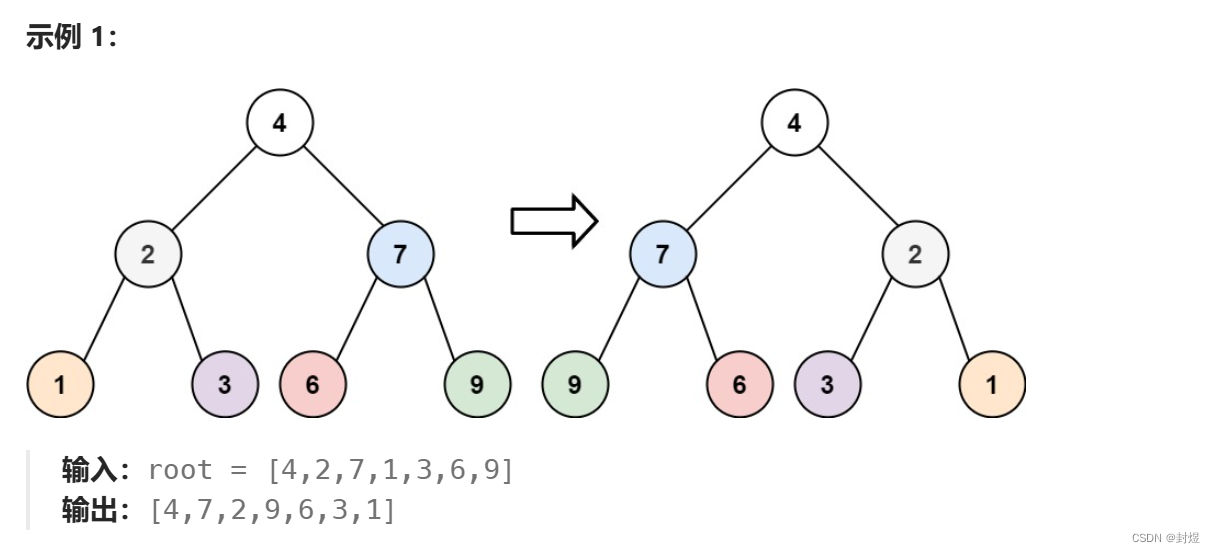
思路:
- 翻转二叉树是把左子树和右子树互换,那么我们每一个子树都要互换。所以我们要不断往子树递归把子树的左子树和右子树交换。这就跟我们的层序遍历一样。
所以我们要递归左右子树,最后再把左右子树交换,然后再返回root。
代码:
struct TreeNode* invertTree(struct TreeNode* root) {if (root == NULL)return NULL;struct TreeNode* left = invertTree(root->left);struct TreeNode* right = invertTree(root->right);root->right = left;root->left = right;return root;
}
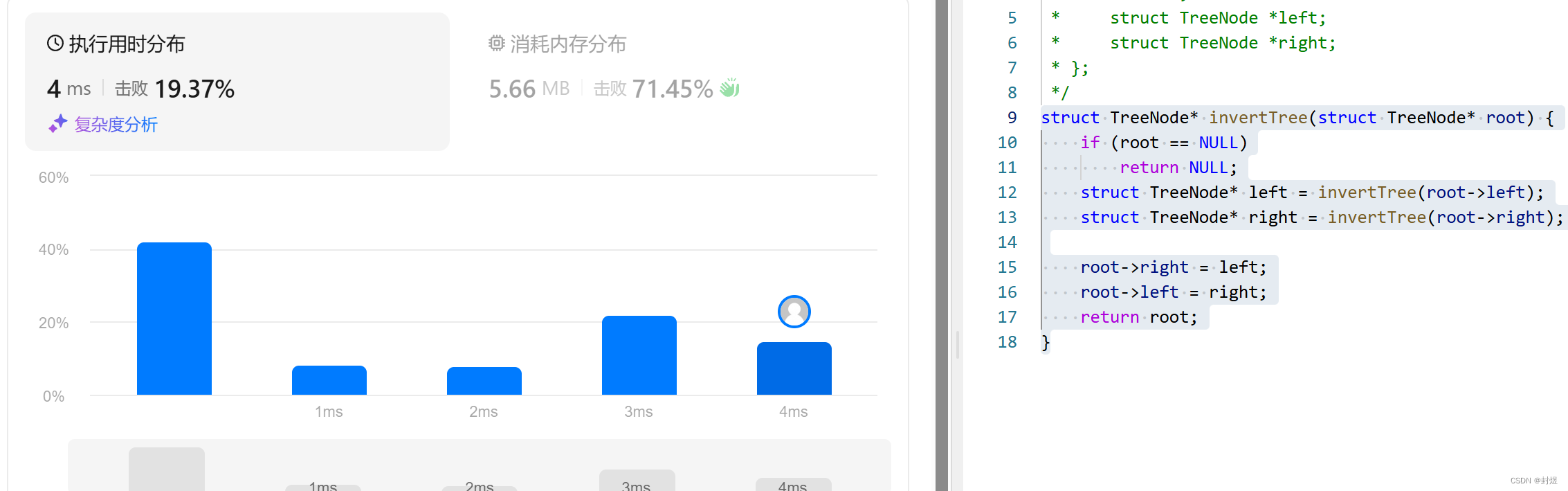
LC572. 另一棵树的子树
- 建议先做一下这道题100. 相同的树
这题其实就是去找和 subRoot 相同的子树。
注意这个例子:我们要保证我们找的 root和 subRoot 左右子树都相同。
所以这时我们要遍历的root的左子树才能判断与subRoot相同。
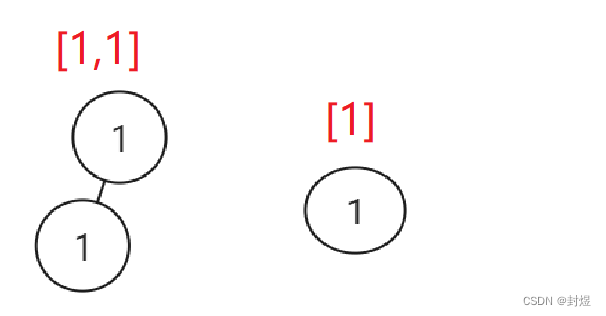
思路:
- 如果 r o o t 和 s u b R o o t 都为 N U L L ,直接返回 t r u e root和subRoot都为NULL,直接返回true root和subRoot都为NULL,直接返回true,如果只有一个为空,返回false,如果此时两个树的val相同,判断此时这个位置是否相同,如果相同直接返回true,不想同去root的左右子树,继续去找。只要找到一个就返回true。
代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL)return true; if (p == NULL || q == NULL)return false;if (p->val != q->val)return false;return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if (root == NULL && subRoot == NULL)return true;if (root == NULL || subRoot == NULL)return false;if (root->val == subRoot->val){if (isSameTree(root,subRoot))return true;}return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}
两道选择题
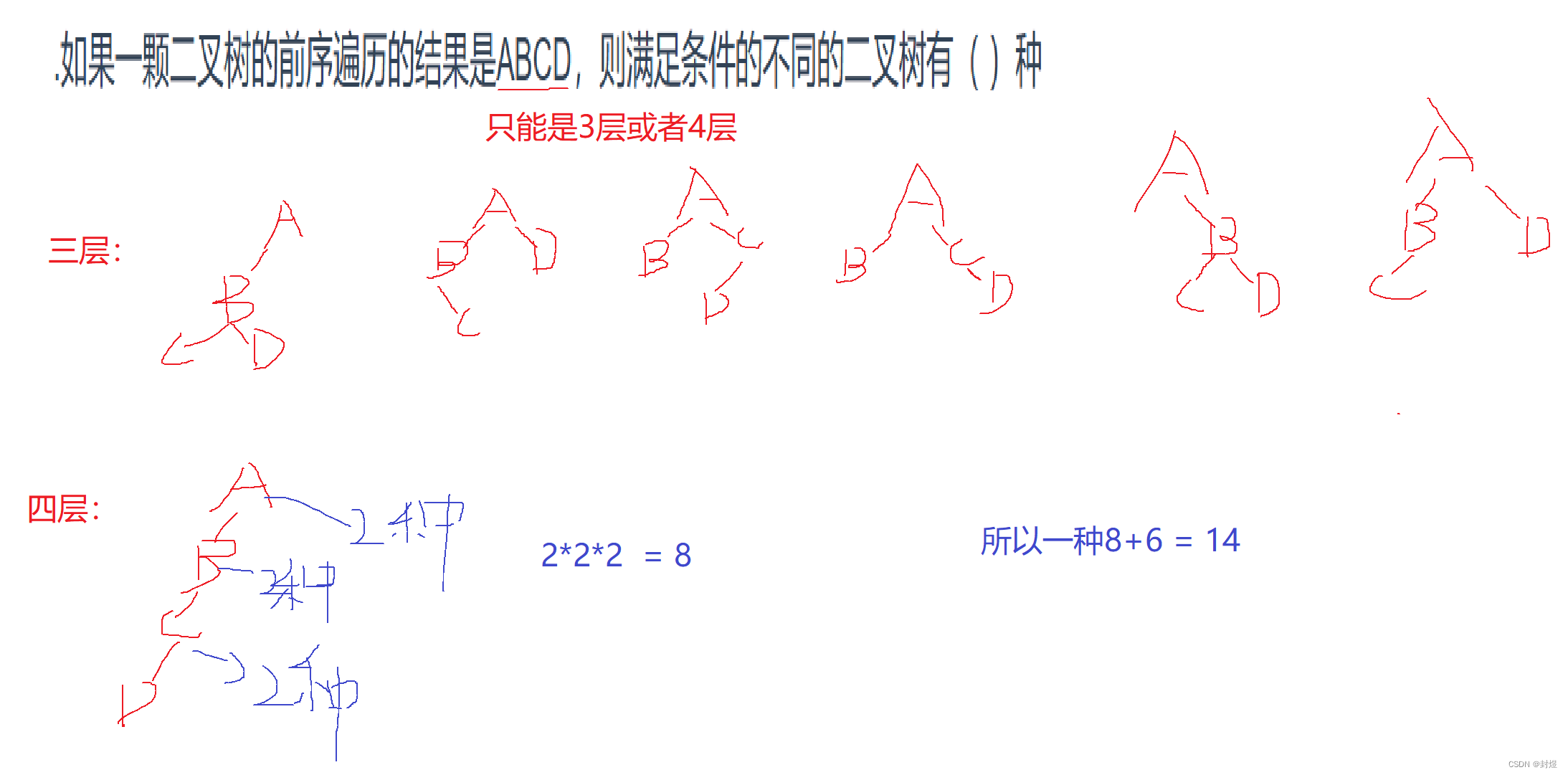

结言
到这里本篇文章就结束了。
本篇文章的基本思路如下:
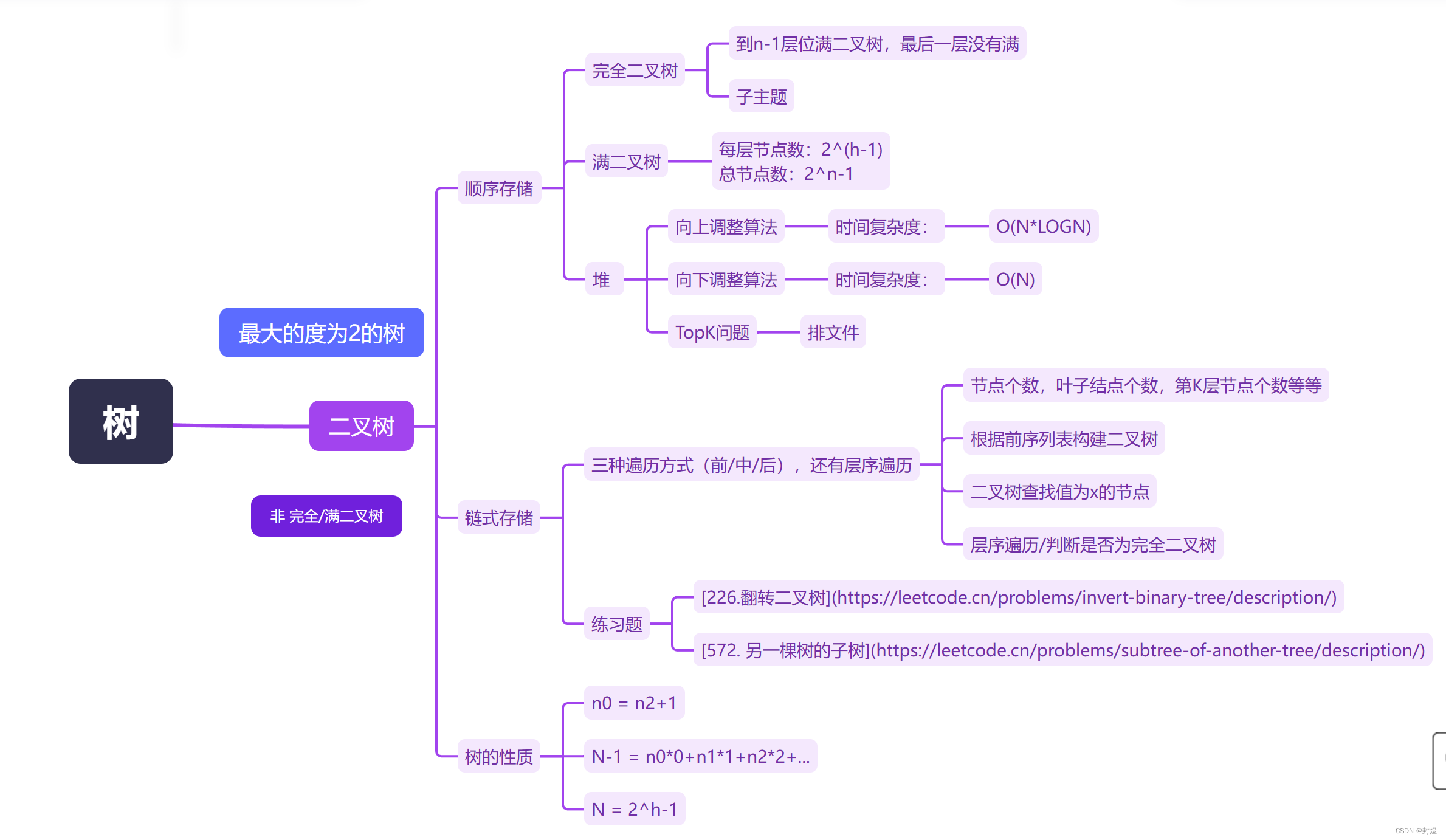
OK,二叉树部分就到这吧,学C++去了。

这篇关于C语言最终文章-二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








