C++ -- 红黑树的基本操作

2024-06-17 17:44
文章标签 c++ 基本操作 红黑树

本文主要是介绍C++ -- 红黑树的基本操作，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

摘要

基本规则

基本操作

利用Graphviz 库

总结

摘要

红黑树是一种自平衡的二叉搜索树，它在插入和删除节点时，通过颜色和旋转操作保持树的平衡，确保插入、删除和查找的时间复杂度都是 (O(log n))。红黑树的每个节点都有一个颜色属性，红色或黑色。通过一些规则，红黑树保持了相对平衡，使得最长路径长度不会超过最短路径长度的两倍。

基本规则

1. 每个节点不是红色就是黑色。
2. 根节点是黑色。
3. 每个叶子节点（NIL节点）是黑色。
4. 如果一个节点是红色的，则它的两个子节点都是黑色的（从每个叶子到根的所有路径上不能有两个连续的红色节点）。
5. 从任一节点到其每个叶子的所有简单路径都包含相同数量的黑色节点。

基本操作

插入操作

#include <iostream>enum Color { RED, BLACK };struct Node {int data;Color color;Node *left, *right, *parent;Node(int data) : data(data), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};class RedBlackTree {
public:RedBlackTree() : root(nullptr) {}void insert(int data) {Node* newNode = new Node(data);root = bstInsert(root, newNode);fixViolation(newNode);}void inorder() { inorderHelper(root); }private:Node* root;Node* bstInsert(Node* root, Node* node) {if (root == nullptr) return node;if (node->data < root->data) {root->left = bstInsert(root->left, node);root->left->parent = root;} else if (node->data > root->data) {root->right = bstInsert(root->right, node);root->right->parent = root;}return root;}void fixViolation(Node* node) {Node* parent = nullptr;Node* grandParent = nullptr;while (node != root && node->color == RED && node->parent->color == RED) {parent = node->parent;grandParent = parent->parent;if (parent == grandParent->left) {Node* uncle = grandParent->right;if (uncle != nullptr && uncle->color == RED) {grandParent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandParent;} else {if (node == parent->right) {rotateLeft(parent);node = parent;parent = node->parent;}rotateRight(grandParent);std::swap(parent->color, grandParent->color);node = parent;}} else {Node* uncle = grandParent->left;if (uncle != nullptr && uncle->color == RED) {grandParent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandParent;} else {if (node == parent->left) {rotateRight(parent);node = parent;parent = node->parent;}rotateLeft(grandParent);std::swap(parent->color, grandParent->color);node = parent;}}}root->color = BLACK;}void rotateLeft(Node* node) {Node* rightNode = node->right;node->right = rightNode->left;if (node->right != nullptr) node->right->parent = node;rightNode->parent = node->parent;if (node->parent == nullptr) root = rightNode;else if (node == node->parent->left) node->parent->left = rightNode;else node->parent->right = rightNode;rightNode->left = node;node->parent = rightNode;}void rotateRight(Node* node) {Node* leftNode = node->left;node->left = leftNode->right;if (node->left != nullptr) node->left->parent = node;leftNode->parent = node->parent;if (node->parent == nullptr) root = leftNode;else if (node == node->parent->left) node->parent->left = leftNode;else node->parent->right = leftNode;leftNode->right = node;node->parent = leftNode;}void inorderHelper(Node* root) {if (root == nullptr) return;inorderHelper(root->left);std::cout << root->data << " ";inorderHelper(root->right);}
};int main() {RedBlackTree tree;tree.insert(10);tree.insert(20);tree.insert(30);tree.insert(15);std::cout << "Inorder traversal of the constructed tree is ";tree.inorder();std::cout << std::endl;return 0;
}

// Output
Inorder traversal of the constructed tree is 10 15 20 3020(B)/    \
10(B)  30(B)\15(R)

插入和删除操作

#include <iostream>
#include <queue>enum Color { RED, BLACK };struct Node {int data;Color color;Node *left, *right, *parent;Node(int data) : data(data), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}Node* sibling() {if (parent == nullptr) return nullptr;return this == parent->left ? parent->right : parent->left;}bool hasRedChild() {return (left != nullptr && left->color == RED) || (right != nullptr && right->color == RED);}
};class RedBlackTree {
public:Node* root;RedBlackTree() : root(nullptr) {}void insert(int data) {Node* newNode = new Node(data);root = bstInsert(root, newNode);fixViolation(newNode);}void deleteNode(int data) {Node* nodeToDelete = search(root, data);if (nodeToDelete == nullptr) return;deleteBSTNode(nodeToDelete);}void inorder() { inorderHelper(root); }void levelOrder() {if (root == nullptr) return;std::queue<Node*> q;q.push(root);while (!q.empty()) {Node* temp = q.front();std::cout << temp->data << " ";q.pop();if (temp->left != nullptr)q.push(temp->left);if (temp->right != nullptr)q.push(temp->right);}}private:Node* bstInsert(Node* root, Node* node) {if (root == nullptr) return node;if (node->data < root->data) {root->left = bstInsert(root->left, node);root->left->parent = root;} else if (node->data > root->data) {root->right = bstInsert(root->right, node);root->right->parent = root;}return root;}Node* search(Node* root, int data) {if (root == nullptr || root->data == data) return root;return data < root->data ? search(root->left, data) : search(root->right, data);}void deleteBSTNode(Node* node) {Node* replacement = BSTreplace(node);bool bothBlack = ((replacement == nullptr || replacement->color == BLACK) && (node->color == BLACK));Node* parent = node->parent;if (replacement == nullptr) {if (node == root) {root = nullptr;} else {if (bothBlack) {fixDoubleBlack(node);} else {if (node->sibling() != nullptr) node->sibling()->color = RED;}if (node == node->parent->left) {node->parent->left = nullptr;} else {node->parent->right = nullptr;}}delete node;return;}if (node->left == nullptr || node->right == nullptr) {if (node == root) {node->data = replacement->data;node->left = node->right = nullptr;delete replacement;} else {if (node == node->parent->left) {parent->left = replacement;} else {parent->right = replacement;}delete node;replacement->parent = parent;if (bothBlack) {fixDoubleBlack(replacement);} else {replacement->color = BLACK;}}return;}std::swap(node->data, replacement->data);deleteBSTNode(replacement);}Node* BSTreplace(Node* node) {if (node->left != nullptr && node->right != nullptr) return successor(node->right);if (node->left == nullptr && node->right == nullptr) return nullptr;return node->left != nullptr ? node->left : node->right;}Node* successor(Node* node) {Node* temp = node;while (temp->left != nullptr) temp = temp->left;return temp;}void fixViolation(Node* node) {Node* parent = nullptr;Node* grandParent = nullptr;while (node != root && node->color == RED && node->parent->color == RED) {parent = node->parent;grandParent = parent->parent;if (parent == grandParent->left) {Node* uncle = grandParent->right;if (uncle != nullptr && uncle->color == RED) {grandParent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandParent;} else {if (node == parent->right) {rotateLeft(parent);node = parent;parent = node->parent;}rotateRight(grandParent);std::swap(parent->color, grandParent->color);node = parent;}} else {Node* uncle = grandParent->left;if (uncle != nullptr && uncle->color == RED) {grandParent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandParent;} else {if (node == parent->left) {rotateRight(parent);node = parent;parent = node->parent;}rotateLeft(grandParent);std::swap(parent->color, grandParent->color);node = parent;}}}root->color = BLACK;}void fixDoubleBlack(Node* node) {if (node == root) return;Node* sibling = node->sibling();Node* parent = node->parent;if (sibling == nullptr) {fixDoubleBlack(parent);} else {if (sibling->color == RED) {parent->color = RED;sibling->color = BLACK;if (sibling == parent->left) {rotateRight(parent);} else {rotateLeft(parent);}fixDoubleBlack(node);} else {if (sibling->hasRedChild()) {if (sibling->left != nullptr && sibling->left->color == RED) {if (sibling == parent->left) {sibling->left->color = sibling->color;sibling->color = parent->color;rotateRight(parent);} else {sibling->left->color = parent->color;rotateRight(sibling);rotateLeft(parent);}} else {if (sibling == parent->left) {sibling->right->color = parent->color;rotateLeft(sibling);rotateRight(parent);} else {sibling->right->color = sibling->color;sibling->color = parent->color;rotateLeft(parent);}}parent->color = BLACK;} else {sibling->color = RED;if (parent->color == BLACK) {fixDoubleBlack(parent);} else {parent->color = BLACK;}}}}}void rotateLeft(Node* node) {Node* rightNode = node->right;node->right = rightNode->left;if (node->right != nullptr) node->right->parent = node;rightNode->parent = node->parent;if (node->parent == nullptr) root = rightNode;else if (node == node->parent->left) node->parent->left = rightNode;else node->parent->right = rightNode;rightNode->left = node;node->parent = rightNode;}void rotateRight(Node* node) {Node* leftNode = node->left;node->left = leftNode->right;if (node->left != nullptr) node->left->parent = node;leftNode->parent = node->parent;if (node->parent == nullptr) root = leftNode;else if (node == node->parent->left) node->parent->left = leftNode;else node->parent->right = leftNode;leftNode->right = node;node->parent = leftNode;}void inorderHelper(Node* root) {if (root == nullptr) return;inorderHelper(root->left);std::cout << root->data << " ";inorderHelper(root->right);}
};int main() {RedBlackTree tree;tree.insert(10);tree.insert(20);tree.insert(30);tree.insert(15);tree.insert(25);tree.insert(5);std::cout << "Inorder traversal of the constructed tree is ";tree.inorder();std::cout << std::endl;tree.deleteNode(20);std::cout << "Inorder traversal after deleting 20 is ";tree.inorder();std::cout << std::endl;std::cout << "Level order traversal of the tree is ";tree.levelOrder();std::cout << std::endl;return 0;
}

// OutputInorder traversal of the constructed tree is 5 10 15 20 25 30 
Inorder traversal after deleting 20 is 5 10 15 25 30 
Level order traversal of the tree is 15 10 30 5 25 15(B)/    \
10(B)  30(B)/     /
5(B)  25(R)

利用Graphviz 库

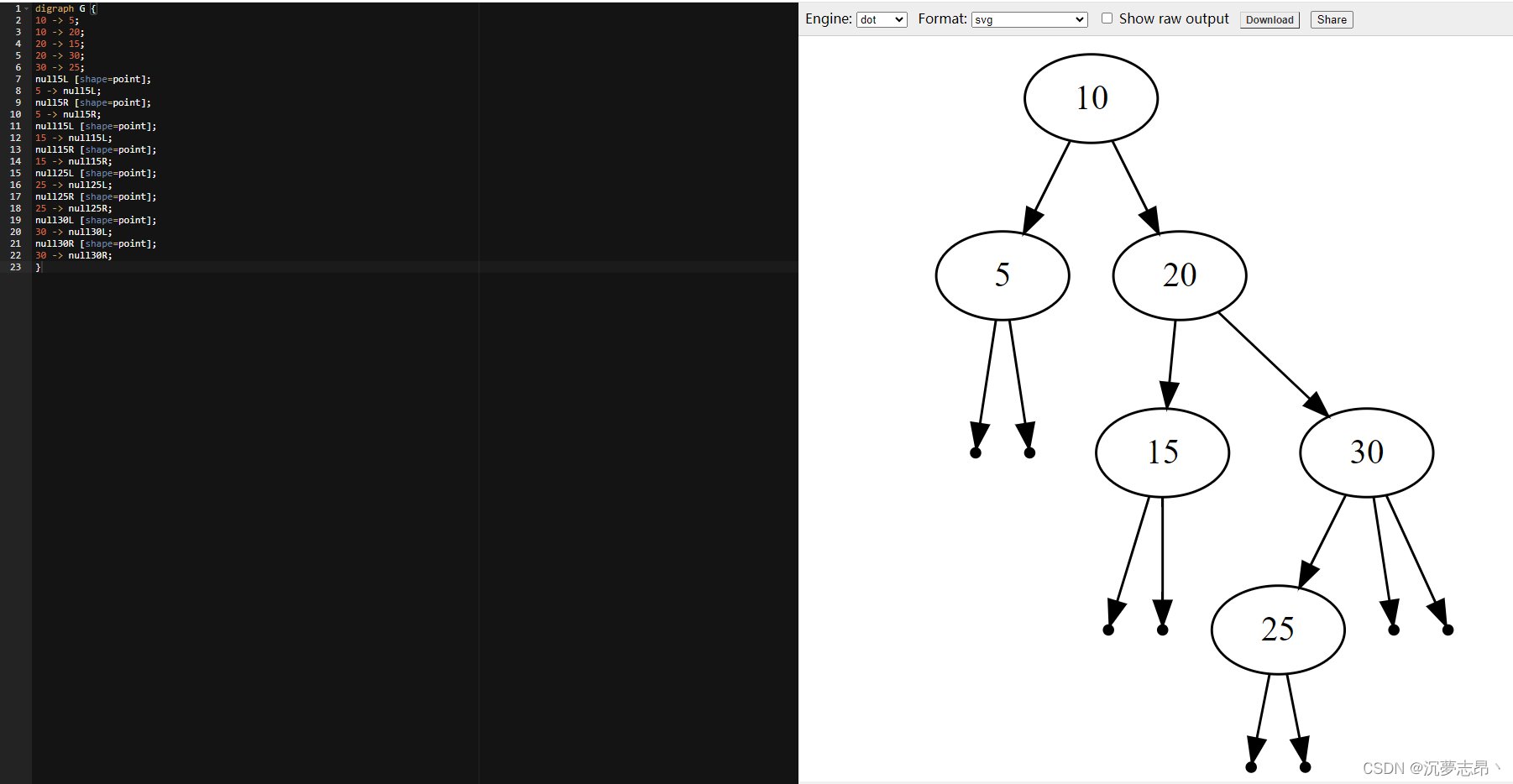
利用 Graphviz 库的图形化表示我们需要生成的红黑树。

Graphviz Online

#include <iostream>
#include <fstream>
#include <queue>enum Color { RED, BLACK };struct Node {int data;Color color;Node *left, *right, *parent;Node(int data) : data(data), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}Node* sibling() {if (parent == nullptr) return nullptr;return this == parent->left ? parent->right : parent->left;}bool hasRedChild() {return (left != nullptr && left->color == RED) || (right != nullptr && right->color == RED);}
};class RedBlackTree {
public:Node* root;RedBlackTree() : root(nullptr) {}void insert(int data) {Node* newNode = new Node(data);root = bstInsert(root, newNode);fixViolation(newNode);}void deleteNode(int data) {Node* nodeToDelete = search(root, data);if (nodeToDelete == nullptr) return;deleteBSTNode(nodeToDelete);}void inorder() { inorderHelper(root); }void levelOrder() {if (root == nullptr) return;std::queue<Node*> q;q.push(root);while (!q.empty()) {Node* temp = q.front();std::cout << temp->data << " ";q.pop();if (temp->left != nullptr)q.push(temp->left);if (temp->right != nullptr)q.push(temp->right);}}void generateGraphviz(const std::string& filename) {std::ofstream file(filename);file << "digraph G {\n";if (root == nullptr) {file << "}\n";return;}generateGraphvizHelper(file, root);file << "}\n";}private:Node* bstInsert(Node* root, Node* node) {if (root == nullptr) return node;if (node->data < root->data) {root->left = bstInsert(root->left, node);root->left->parent = root;} else if (node->data > root->data) {root->right = bstInsert(root->right, node);root->right->parent = root;}return root;}Node* search(Node* root, int data) {if (root == nullptr || root->data == data) return root;return data < root->data ? search(root->left, data) : search(root->right, data);}void deleteBSTNode(Node* node) {Node* replacement = BSTreplace(node);bool bothBlack = ((replacement == nullptr || replacement->color == BLACK) && (node->color == BLACK));Node* parent = node->parent;if (replacement == nullptr) {if (node == root) {root = nullptr;} else {if (bothBlack) {fixDoubleBlack(node);} else {if (node->sibling() != nullptr) node->sibling()->color = RED;}if (node == node->parent->left) {node->parent->left = nullptr;} else {node->parent->right = nullptr;}}delete node;return;}if (node->left == nullptr || node->right == nullptr) {if (node == root) {node->data = replacement->data;node->left = node->right = nullptr;delete replacement;} else {if (node == node->parent->left) {parent->left = replacement;} else {parent->right = replacement;}delete node;replacement->parent = parent;if (bothBlack) {fixDoubleBlack(replacement);} else {replacement->color = BLACK;}}return;}std::swap(node->data, replacement->data);deleteBSTNode(replacement);}Node* BSTreplace(Node* node) {if (node->left != nullptr && node->right != nullptr) return successor(node->right);if (node->left == nullptr && node->right == nullptr) return nullptr;return node->left != nullptr ? node->left : node->right;}Node* successor(Node* node) {Node* temp = node;while (temp->left != nullptr) temp = temp->left;return temp;}void fixViolation(Node* node) {Node* parent = nullptr;Node* grandParent = nullptr;while (node != root && node->color == RED && node->parent->color == RED) {parent = node->parent;grandParent = parent->parent;if (parent == grandParent->left) {Node* uncle = grandParent->right;if (uncle != nullptr && uncle->color == RED) {grandParent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandParent;} else {if (node == parent->right) {rotateLeft(parent);node = parent;parent = node->parent;}rotateRight(grandParent);std::swap(parent->color, grandParent->color);node = parent;}} else {Node* uncle = grandParent->left;if (uncle != nullptr && uncle->color == RED) {grandParent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandParent;} else {if (node == parent->left) {rotateRight(parent);node = parent;parent = node->parent;}rotateLeft(grandParent);std::swap(parent->color, grandParent->color);node = parent;}}}root->color = BLACK;}void fixDoubleBlack(Node* node) {if (node == root) return;Node* sibling = node->sibling();Node* parent = node->parent;if (sibling == nullptr) {fixDoubleBlack(parent);} else {if (sibling->color == RED) {parent->color = RED;sibling->color = BLACK;if (sibling == parent->left) {rotateRight(parent);} else {rotateLeft(parent);}fixDoubleBlack(node);} else {if (sibling->hasRedChild()) {if (sibling->left != nullptr && sibling->left->color == RED) {if (sibling == parent->left) {sibling->left->color = sibling->color;sibling->color = parent->color;rotateRight(parent);} else {sibling->left->color = parent->color;rotateRight(sibling);rotateLeft(parent);}} else {if (sibling == parent->left) {sibling->right->color = parent->color;rotateLeft(sibling);rotateRight(parent);} else {sibling->right->color = sibling->color;sibling->color = parent->color;rotateLeft(parent);}}parent->color = BLACK;} else {sibling->color = RED;if (parent->color == BLACK) {fixDoubleBlack(parent);} else {parent->color = BLACK;}}}}}void rotateLeft(Node* node) {Node* rightNode = node->right;node->right = rightNode->left;if (node->right != nullptr) node->right->parent = node;rightNode->parent = node->parent;if (node->parent == nullptr) root = rightNode;else if (node == node->parent->left) node->parent->left = rightNode;else node->parent->right = rightNode;rightNode->left = node;node->parent = rightNode;}void rotateRight(Node* node) {Node* leftNode = node->left;node->left = leftNode->right;if (node->left != nullptr) node->left->parent = node;leftNode->parent = node->parent;if (node->parent == nullptr) root = leftNode;else if (node == node->parent->left) node->parent->left = leftNode;else node->parent->right = leftNode;leftNode->right = node;node->parent = leftNode;}void inorderHelper(Node* root) {if (root == nullptr) return;inorderHelper(root->left);std::cout << root->data << " ";inorderHelper(root->right);}void generateGraphvizHelper(std::ofstream& file, Node* root) {if (root->left != nullptr) {file << root->data << " -> " << root->left->data << ";\n";generateGraphvizHelper(file, root->left);} else {file << "null" << root->data << "L [shape=point];\n";file << root->data << " -> null" << root->data << "L;\n";}if (root->right != nullptr) {file << root->data << " -> " << root->right->data << ";\n";generateGraphvizHelper(file, root->right);} else {file << "null" << root->data << "R [shape=point];\n";file << root->data << " -> null" << root->data << "R;\n";}}
};int main() {RedBlackTree tree;tree.insert(10);tree.insert(20);tree.insert(30);tree.insert(15);tree.insert(25);tree.insert(5);tree.generateGraphviz("rbtree.dot");std::cout << "Graphviz dot file generated as rbtree.dot" << std::endl;return 0;
}

// Output
digraph G {
10 -> 5;
10 -> 20;
20 -> 15;
20 -> 30;
30 -> 25;
null5L [shape=point];
5 -> null5L;
null5R [shape=point];
5 -> null5R;
null15L [shape=point];
15 -> null15L;
null15R [shape=point];
15 -> null15R;
null25L [shape=point];
25 -> null25L;
null25R [shape=point];
25 -> null25R;
null30L [shape=point];
30 -> null30L;
null30R [shape=point];
30 -> null30R;
}10/  \
5    20/  \15  30/25

总结

红黑树（Red-Black Tree）是一种自平衡二叉搜索树，常用于需要高效插入、删除和查找操作的数据结构中。红黑树的特点包括每个节点是红色或黑色、根节点是黑色、红色节点的子节点必须是黑色、从任一节点到其每个叶子节点的路径上的黑色节点数目相同。

这篇关于C++ -- 红黑树的基本操作的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1070122。

相关文章

C++ 中的 if-constexpr语法和作用

C++ 中的 if-constexpr语法和作用

《C++中的if-constexpr语法和作用》if-constexpr语法是C++17引入的新语法特性,也被称为常量if表达式或静态if（staticif）,：本文主要介绍C++中的if-c... 目录1 if-constexpr 语法1.1 基本语法1.2 扩展说明1.2.1 条件表达式1.2.2 fa
阅读更多...
C++中::SHCreateDirectoryEx函数使用方法

C++中::SHCreateDirectoryEx函数使用方法

《C++中::SHCreateDirectoryEx函数使用方法》::SHCreateDirectoryEx用于创建多级目录,类似于mkdir-p命令,本文主要介绍了C++中::SHCreateDir... 目录1. 函数原型与依赖项2. 基本使用示例示例 1：创建单层目录示例 2：创建多级目录3. 关键注
阅读更多...
C++从序列容器中删除元素的四种方法

C++从序列容器中删除元素的四种方法

《C++从序列容器中删除元素的四种方法》删除元素的方法在序列容器和关联容器之间是非常不同的,在序列容器中,vector和string是最常用的,但这里也会介绍deque和list以供全面了解,尽管在一... 目录一、简介二、移除给定位置的元素三、移除与某个值相等的元素3.1、序列容器vector、deque
阅读更多...
C++常见容器获取头元素的方法大全

C++常见容器获取头元素的方法大全

《C++常见容器获取头元素的方法大全》在C++编程中,容器是存储和管理数据集合的重要工具,不同的容器提供了不同的接口来访问和操作其中的元素,获取容器的头元素（即第一个元素）是常见的操作之一,本文将详细... 目录一、std::vector二、std::list三、std::deque四、std::forwa
阅读更多...
C++字符串提取和分割的多种方法

C++字符串提取和分割的多种方法

《C++字符串提取和分割的多种方法》在C++编程中,字符串处理是一个常见的任务,尤其是在需要从字符串中提取特定数据时,本文将详细探讨如何使用C++标准库中的工具来提取和分割字符串,并分析不同方法的适用... 目录1. 字符串提取的基本方法1.1 使用 std::istringstream 和 >> 操作符示
阅读更多...
C++原地删除有序数组重复项的N种方法

C++原地删除有序数组重复项的N种方法

《C++原地删除有序数组重复项的N种方法》给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度,不要使用额外的数组空间,你必须在原地修改输入数组并在使用O(... 目录一、问题二、问题分析三、算法实现四、问题变体：最多保留两次五、分析和代码实现5.1、问题分析5.
阅读更多...
C++ 各种map特点对比分析

C++ 各种map特点对比分析

《C++各种map特点对比分析》文章比较了C++中不同类型的map（如std::map,std::unordered_map,std::multimap,std::unordered_multima... 目录特点比较C++ 示例代码 ​​​​​​代码解释特点比较1. std::map底层实现：基于红黑
阅读更多...
C++中函数模板与类模板的简单使用及区别介绍

C++中函数模板与类模板的简单使用及区别介绍

《C++中函数模板与类模板的简单使用及区别介绍》这篇文章介绍了C++中的模板机制,包括函数模板和类模板的概念、语法和实际应用,函数模板通过类型参数实现泛型操作,而类模板允许创建可处理多种数据类型的类,... 目录一、函数模板定义语法真实示例二、类模板三、关键区别四、注意事项 ‌在C++中，模板是实现泛型编程
阅读更多...
利用Python和C++解析gltf文件的示例详解

利用Python和C++解析gltf文件的示例详解

《利用Python和C++解析gltf文件的示例详解》gltf,全称是GLTransmissionFormat,是一种开放的3D文件格式,Python和C++是两个非常强大的工具,下面我们就来看看如何... 目录什么是gltf文件选择语言的原因安装必要的库解析gltf文件的步骤1. 读取gltf文件2. 提
阅读更多...
C++快速排序超详细讲解

C++快速排序超详细讲解

《C++快速排序超详细讲解》快速排序是一种高效的排序算法,通过分治法将数组划分为两部分,递归排序,直到整个数组有序,通过代码解析和示例,详细解释了快速排序的工作原理和实现过程,需要的朋友可以参考下... 目录一、快速排序原理二、快速排序标准代码三、代码解析四、使用while循环的快速排序1.代码代码1.由快
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2