本文主要是介绍计算机组成原理第二章数据的表示和运算(数制与编码),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
数据的表示和运算
考纲内容
复习提示
2.1数制与编码
2.1.1进位计数制及其相互转换
1.进位计数法
2.不同进制数之间的相互转换
2.1.2定点数的编码表示
1.真值和机器数
2.机器数的定点表示
3.原码、补码、反码、移码
2.1.3整数的表示
1.无符号整数的表示
2.有符号整数的表示
2.1.4C语言中的整数类型及类型转换
1.C语言中的整型数据类型
2.有符号数和无符号数的转换
3.不同字长整数之间的转换
数据的表示和运算
考纲内容
(一)数制与编码
进位计数制及其相互转换;定点数的编码表示
(二)运算方法和运算电路
基本运算部件:加法器;算术逻辑单元(ALU)
加/减运算:补码加/减运算器;标志位的生成
乘/除运算:乘/除法运算的基本原理;乘法电路和除法电路的基本结构
(三)整数的表示和运算
无符号整数的表示和运算;有符号整数的表示和运算
(四)浮点数的表示和运算
浮点数的表示:IEEE 754标准;浮点数的加/减运算
复习提示
本章内容较为繁杂,由于计算机中数的表示和运算方法与人们日常生活中的表示和运算方法不同,因此理解也较为困难。纵观历年统考真题,不难发现unsigned、short、int、long、float、double等在C语言中的表示、运算、溢出判断、隐式类型转换、强制类型转换、IEEE 754 浮点数的表示,以及浮点数的运算,都是考研考查的重点,需要牢固掌握。
在学习本章时,请读者思考以下问题:
1) 在计算机中,为什么要采用二进制来表示数据?
2) 计算机在字长足够的情况下能够精确地表示每个数吗? 若不能,请举例说明。
3) 字长相同的情况下,浮点数和定点数的表示范围与精度有什么区别?
4) 用移码表示浮点数的阶码有什么好处?
请读者在本章的学习过程中寻找答案,本章末尾会给出参考案。
2.1数制与编码
2.1.1进位计数制及其相互转换
【命题追踪——采用二进制编码的原因(2018)】
在计算机系统内部,所有信息都是用二进制进行编码的,这样做的原因有以下几点。
1) 二进制只有两种状态,使用有两个稳定状态的物理器件就可以表示二进制数的每一位,制造成本比较低,例如用高低电平或电荷的正负极性都可以很方便地表示0和1。
2) 二进制位1和0正好与逻辑值“真”和“假”相对应,为计算机实现逻辑运算和程序中的逻辑判断提供了便利条件。
3) 二进制的编码和运算规则都很简单,通过逻辑门电路能方便地实现算术运算。
1.进位计数法
常用的进位计数法有十进制、二进制、八进制、十六进制等。十进制数是日常生活中最常使用的,而计算机中通常使用二进制数、八进制数和十六进制数。
在进位计数法中,每个数位所用到的不同数码的个数称为基数。十进制的基数为 10(0~9),每个数位计满 10 就向高位进位,即“逢十进一”。十进制数 101,其个位的1显然与百位的1所表示的数值是不同的。
每个数码所表示的数值等于该数码本身乘以一个与它所在数位有关的常数,这个常数称为位权。一个进位数的数值大小就是它的各位数码按权相加。
一个 r 进制数(KₙK ₙ₋₁….K₀K₋₁...K₋ₘ")的数值可表示为
式中,r 是基数;rⁱ 是第 i 位的位权;Kᵢ 的取值可以是 0,1,…,r-1共r个数码中的任意一个。
1) 二进制。计算机中用得最多的是基数为 2 的计数制,即二进制。二进制只有0和1两种数码,计数“逢二进一”。它的任意数位的权为2ⁱ ,i为所在位数。
2) 八进制。基数为 8,有0~7共8个不同的数码。计数逢八进一。因为r=8=2³,所以把二进制中的3位数码编为一组就是1位八进制数码,两者之间的转换极为方便。
3) 十六进制。基数为 16,有 0~9、A~F 共 16 个不同的数码,其中 A~F 分别表示 10~15。计数逢十六进一。因为r=16=2⁴,所以4 位二进制数码与1位十六进制数码相对应。
可以用后缀字母标识一个数的进位计数制,用B表示二进制,用O表示八进制,用D表示十进制(通常直接省略),用H表示十六进制,有时也用前缀 0x 表示十六进制数。
2.不同进制数之间的相互转换
这部分我会放在一个章节单独讲解,详细可以查看下面的链接
不同进制数的前后缀表示以及他们之间的相互转换(全面解析版)![]() http://t.csdnimg.cn/kPyrj
http://t.csdnimg.cn/kPyrj
2.1.2定点数的编码表示
1.真值和机器数
在日常生活中,通常用正号、负号来分别表示正数(正号可省略)和负数,如+15、-8等。这种带“+”或“-”符号的数称为真值。真值是机器数所代表的实际值。
在计算机中,通常将数的符号和数值部分一起编码,将数据的符号数字化,通常用“0”表示“正”,用“1”表示“负”。这种把符号“数字化”的数称为机器数。常用的有原码、补码和反码表示法。如0,101(这里的逗号“,”仅为区分符号位与数值位)表示+5。
2.机器数的定点表示
根据小数点的位置是否固定,在计算机中有两种数据格式:定点表示和浮点表示。在现代计算机中,通常用补码整数表示整数,用原码小数表示浮点数的尾数部分,用移码表示浮点数的阶码部分,历年统考真题的命题信息也主要落在这个范畴之内。
定点表示法用来表示定点小数和定点整数。
1) 定点小数。定点小数是纯小数,约定小数点位置在符号位之后、有效数值部分最高位之前。若数据X的形式为X=x₀x₁x₂...xₙ (其中x₀为符号位,x₁~xₙ是数值的有效部分,也称尾数,x₁为最高有效位),则在计算机中的表示形式如图 2.1所示。
2) 定点整数。定点整数是纯整数,约定小数点位置在有效数值部分最低位之后。若数据X的形式为X=x₀x₁x₂...xₙ (其中x₀为符号位,x₁~xₙ是尾数,xₙ为最低有效位)则在计算机中的表示形式如图 2.2 所示。

事实上,在机器内部并没有小数点,只是人为约定了小数点的位置。因此,在定点数的编码和运算中不用考虑对应的定点数是小数还是整数,而只需关心它们的符号位和数值位即可。
定点数的编码表示法主要有以下4种:原码、补码、反码和移码。
3.原码、补码、反码、移码
(1)原码表示法
用机器数的最高位表示数的符号,其余各位表示数的绝对值。原码的定义如下。
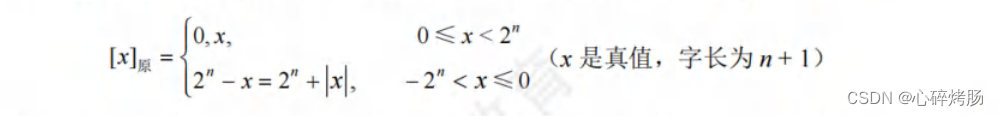
例如,若x₁= +1110,x₂= -1110,字长为8位,则其原码表示为[x₁]原 = 0,0001110,[x₂]原 = 2⁷+1110=1,0001110,其中最高位是符号位。
若字长为 n+ 1,则原码整数的表示范围为 -(2ⁿ - 1) ≤ x ≤ 2ⁿ-1(关于原点对称)。
注意:零的原码表示有正零和负零两种形式,即[+0]原 = 00000000 和 [-0]原 = 10000000。
原码表示的优点:①与真值的对应关系简单、直观,与真值的转换简单;②用原码实现乘除运算比较简便。
缺点:① 0的表示不唯一,有±0 两个编码;② 原码加减运算比较复杂。在原码加减运算中,对于两个不同符号数的加法(或同符号数的减法),先要比较两个数的绝对值大小,然后用绝对值大的数减去绝对值小的数,最后还要为结果选择合适的符号。
(2)补码表示法
补码表示法中的加减运算统一采用加法操作实现。正数的补码和原码相同,负数的补码等于模(n+1位补码的模为2ⁿ⁺¹)与该负数绝对值之差。补码的定义如下:
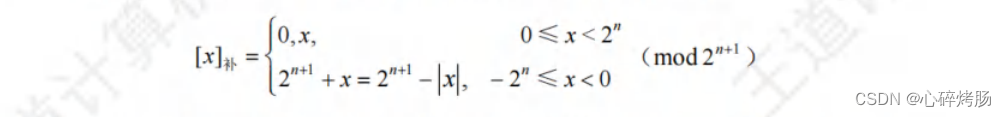
综合上述定义可知,无论是正数还是负数,[x]补=2ⁿ⁺¹+x (-2ⁿ ≤x< 2ⁿ,mod 2ⁿ⁺¹)。
例如,若x₁= +1010,x₂= -1101,字长为8位,则其补码表示为[x₁]补=0,0001010,[x₂]补=2⁸ - 0,0001101=1,1110011。
【命题追踪——补码的表示范围(2010、2013、2014、2022)】
若字长为 n+1,则补码整数的表示范围为-2ⁿ≤x≤2ⁿ-1(比原码多表示“-2ⁿ”)。
● 几个特殊数据的补码表示:
- 1) [+0]补 = [-0]补 = 0,00...0 (含符号位共 n+1 个0),说明 0 的补码表示是唯一的。
- 2) [-1]补 = 2ⁿ⁺¹-1 = 1,11...1(含符号位共n+1个1)。
- 3) [2ⁿ-1]补 = 0,11..1(n个1),即n+1位补码能表示的最大整数。
- 4) [-2ⁿ]补 = 1,00...0(n个0),即n+1位补码能表示的最小整数。
● 模运算:
在模运算中,一个数与它除以“模”后得到的余数是等价的,如 A、B、M 满足A=B+K×M(K为整数),则记为A≡B(mod M),即 A、B各除以 M后的余数相同。在补码运算中,[A]补-[B]补=[A]补 + M-[B]补,而 M-[B]补 = [-B]补,因此补码可以借助加法运算来实现减法运算。
● 补码与真值之间的转换:
【命题追踪——补码和真值的相互转换(2020、2023)】
真值转换为补码:对于正数,与原码的方式一样。对于负数,符号位取1,其余各位由真值 “各位取反,末位加1” 得到。
补码转换为真值:若符号位为0,与原码的方式一样。
若符号位为1,真值的符号为负,数值部分各位由补码 “各位取反,末位加1” 得到。
● 变形补码
变形补码是一种采用双符号位的补码表示,也称 模4补码。假定变形补码的位数为n+1(其中符号位占2位,数值位占n-1位),则整数变形补码的表示为
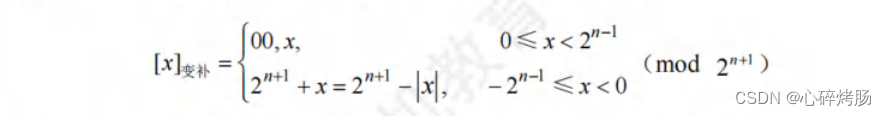
模4补码双符号位 00 表示正,11表示负,用在执行算术运算的 ALU 中。
(3)反码表示法(了解)
负数的补码可采用“各位取反,末位加1”的方法得到,若仅各位求反而末尾不加 1,则是负数的反码表示,因此负数反码的定义就是在相应的补码表示中再末位减 1。
正数反码的定义和相应的补码(或原码)表示相同。
反码表示存在以下几个方面的不足:
① 0 的表示不唯一(即存在±0);
② 表示范围比补码少一个最小负数。反码在计算机中很少使用,通常用作数码变换的中间表示形式。
(4)移码表示法
移码常用来表示浮点数的阶码,它只能表示整数。
移码就是在真值X上加上一个常数(偏置值),通常这个常数取 2ⁿ,相当于X在数轴上向正方向偏移了若干单位,这就是“移码”一词的由来。移码的定义如下。
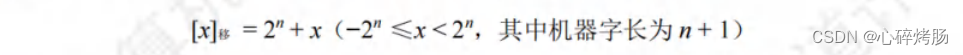
例如,若正数x₁= +10101,x₂= -10101,字长为8位,则其移码表示为[x₁]移=2⁷+10101=1,0010101;[x₂]补= 2⁷+(-10101)=0,1101011。
移码具有以下特点:
① 移码中零的表示唯一,[+0]移=2ⁿ + 0 = [-0]移 = 2ⁿ - 0=100...0(n个“0”)。
② 一个真值的移码和补码仅差一个符号位,[x]补的符号位取反即得[x]移(“1”表示正,“0”表示负,这与其他机器数的符号位取值正好相反),反之亦然。
③ 移码全 0 时,对应真值的最小值-2ⁿ;移码全1时,对应真值的最大值 2ⁿ-1。
④ 移码保持了数据原有的大小顺序,移码大真值就大,移码小真值就小。
原码、补码、反码和移码这 4种编码表示的总结如下:
【命题追踪——补码大小的判断(2015)】
- ① 原码、补码、反码的符号位相同,正数的机器码相同。
- ② 原码、反码的表示在数轴上对称,二者都存在 +0 和 -0 两个 0。
- ③ 补码、移码的表示在数轴上不对称,零的表示唯一,它们比原码、反码多表示一个数。
- ④ 整数的补码、移码的符号位相反,数值位相同。
- ⑤ 负数的补码、反码末位相差1。
- ⑥ 原码很容易判断大小。而负数的补码、反码很难直接判断大小,可采用如下规则快速判断:对于负数,数值位部分越小,其绝对值越大,即负得越多。
2.1.3整数的表示
1.无符号整数的表示
【命题追踪——机器码与补码、无符号数之间的转换(2021)】
当一个编码的全部二进制位均为数值位而没有符号位时,该编码表示就是无符号整数,简称无符号数。此时,默认数的符号为正。
因为无符号整数省略了一位符号位,所以在字长相同的情况下,它能表示的最大数比有符号整数能表示的大。
一般在全部是正数运算且不出现负值结果的场合下,使用无符号整数表示。例如,可用无符号整数进行地址运算,或用它来表示指针。
例如,对于8位无符号整数,最小数为0000 0000(值为0),最大数为1111 1111(值为2⁸-1=255),即表示范围为0~255;
而对于8位有符号整数,最小数为1000 0000(值为-2⁷= -128),最大数为 0111 1111(值为2⁷-1=127),即表示范围为-128~127。
2.有符号整数的表示
将符号数值化,并将符号位放在有效数字的前面,就组成了有符号整数。虽然前面介绍的原码、补码、反码和移码都可以用来表示有符号整数,但补码表示有其明显的优势:
① 与原码和反码相比,0的补码表示唯一。
②与原码和移码相比,补码运算规则比较简单,且符号位可以和数值位一起参加运算。
③ 与原码和反码相比,补码比原码和反码多表示一个最小负数。
计算机中的有符号整数都用补码表示,故n位有符号整数的表示范围是 -2ⁿ⁻¹~2ⁿ⁻¹- 1。
2.1.4C语言中的整数类型及类型转换
1.C语言中的整型数据类型
【命题追踪——int 型数据的表示范围(2017、2019)】
C语言中的整型数据就是定点整数,根据位数的不同,可分为字符型(char,8位)、短整型(short 或 shont int, 16 位)、整型(int,32 位)、
长整型(long 或 long int,在 32 位机器中为 32位,在 64 位机器中为 64 位)。
char 是整型数据中比较特殊的一种,其他如 short/int/long 等不指定signed/unsigned 时都默认是有符号整数,但 char 默认是无符号整数。
无符号整数(unsigned short/intlong)的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
signed/unsigned 整型数据都是按补码形式存储的,只是 signed 型的最高位代表符号位,而在unsigned 型中表示数值位,因此这两者所表示的数据范围也有所不同。
2.有符号数和无符号数的转换
【命题追踪——有符号数与无符号数的相互转换(2011、2016、2019)】
C语言允许在不同的数据类型之间做类型转换。
强制类型转换格式为“TYPE b=(TYPE) a”,强制类型转换后,返回一个具有 TYPE 类型的数值,这种操作并不会改变操作数本身。
先看由 short 型转换到 unsigned short 型的情况。考虑如下代码片段:
int main(){
short x= -4321;
unsigned short y=(unsigned short) x;
printf("x=%d,y=%u\n",x,y);
}有符号数 x 是一个负数,而无符号数 y 的表示范围显然不包括 x 的值。
在采用补码的机器上,上述程序会输出如下结果:
x = -4321,y = 61215输出的结果中,得到的 y 值似乎与原来的 x 没有一点关系。不过将这两个数转换为二进制表示时,我们就会发现其中的规律,如表 2.1所示。
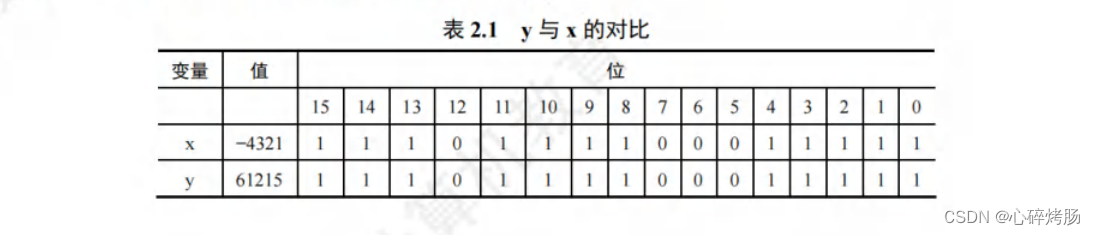
观察可知,将 short 型强制转换为 unsigned short 型只改变数值,而两个变量对应的每位都是一样的。
通过本例可知,强制类型转换的结果是保持位值不变,仅改变了解释这些位的方式。
再看由 unsigned short 型转换到 short 型的情况。考虑如下代码片段:
int main(){
unsigned short x=65535;
short y= (short)x;
printf("x=%u,y=%d\n",x,y);
}同样在采用补码的机器上,上述程序会输出如下结果:
x = 65535,y = -1把这两个数转换为二进制表示,同样可以证实之前的结论。
因此,有符号数转换为等长的无符号数时,符号位解释为数值的一部分,负数转换为无符号数时数值将发生变化。
同理,无符号数转换为有符号数时最高位解释为符号位,也可能发生数值的变化。
注意:若同时有无符号数和有符号数参与运算,则C语言标准规定按无符号数进行运算
3.不同字长整数之间的转换
【命题追踪——无符号数的零扩展(2012)】
另一种常见的运算是在不同字长的整数之间进行类型转换。
先看大字长变量向小字长变量转换的情况。考虑如下代码片段:
int main(){
int x=165537,u=-34991; //int型占用4B
short y=(short)x,v=(short)u; //short型占用2B
printf("x=%d,y=%d\n", x, y);
printf("u=%d,v=%d\n", u, v);
}
运行结果如下:
x = 165537, y = -31071u = -34991, v = 30545其中 x,y,u,v的十六进制表示分别为 0x000286a1,0x86a1,0xffff07751,0x7751,观察上述数字很容易得出结论,当大字长变量向小字长变量强制类型转换时,系统把多余的高位部分直接截断,低位部分直接赋值,因此也是一种保持位值的处理方法。
再看小字长变量向大字长变量转换的情况。考虑如下代码片段:
int main(){
short x=-4321;
int y=x;
unsigned short u=(unsigned short)x;
unsigned int v=u;
printf("x=%d,y=%d\n", x, y);
printf("u=%u,v=%u\n", u, v);
}运行结果如下:
x = -4321, y = -4321
u = 61215, v = 61215【命题追踪——无符号数的零扩展(2012),补码的符号扩展(2021)】
x,y,u,v的十六进制表示分别为 0xef1f,0xffffef1f,0xef1f,0x0000ef1f。
由本例可知,小字长到大字长的转换时,不仅要使相应的位值相等,还要对高位部分进行扩展。
若原数字是无符号整数,则进行零扩展,扩展后的高位部分用0填充。否则进行符号扩展,扩展后的高位部分用原数字符号位填充。
其实两种方式扩展的高位部分都可理解为原数字的符号位。
这与之前的三个例子都不一样,从位值与数值的角度看,前三个例子的转换规则都是保证相应的位值相等,而小字长向大字长的转换,在位值相等的条件下还要补充高位的符号位,可以理解为数值的相等。
注意,char 型为 8 位无符号整数,其在转换为 int 型时高位补0即可。
这篇关于计算机组成原理第二章数据的表示和运算(数制与编码)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






