本文主要是介绍《全网首发》平衡三进制图灵机的构建,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
PS:以下内容均为本人原创,未经授权及许可,严禁引图、转载或加工,违者必究。
————2024年6月13号
1、图灵机的概述
图灵机(Turing machine)是一种理论计算模型,由英国数学家阿兰·图灵(Alan Turing)于1936年提出。它被用来研究计算过程的基本性质和计算理论的极限。图灵机被认为是现代计算机的理论基础。
1.1图灵机的组成部分:
- 无限长的纸带: 纸带被划分成一系列的方格,每个方格可以包含一个符号(例如0或1),纸带既可以向左也可以向右移动。
- 读写头: 读写头可以在纸带上移动,读取或写入符号。
- 状态寄存器: 状态寄存器存储着图灵机当前的状态。状态是有限的,可以是预定义的某一个状态集合中的一个。
- 状态转移函数: 这是一组规则,决定了图灵机在给定状态和读取到的符号时如何行动。规则包括:
- 写入符号
- 移动读写头(向左或向右)
- 进入下一个状态
1.2图灵机的运行过程:
- 读写头读取纸带上的当前符号。
- 根据当前符号和当前状态,查找状态转移函数,决定接下来要执行的操作。
- 执行操作,更新纸带上的符号,移动读写头,更新状态寄存器中的状态。
- 重复上述步骤,直到达到某个停止状态(如果有的话)。
图灵机的主要意义在于它能够模拟任何计算过程,因此被称为通用图灵机(Universal Turing Machine)。任何可以被计算的问题,理论上都可以由图灵机来解决。这使得图灵机成为计算理论中的一个重要工具,用来定义和研究可计算性、算法的复杂性以及计算的极限。
2、平衡三进制图灵机的感想来源
平时就喜欢逛blbl看看科普视频,是《苏联的三进制电脑》差评君写的,好像是几年前的视频了,那时就想那么厉害的东西没了真可惜,后面又看到很多人去辩论,呈现两边极化的现象,可见都没见过这东西,真不好评价。后面又详细的查了一下前苏联的资料,发现这东西是真的有趣,还发现很多人都想重新将这三进制计算捞回来。
但是,三进制是它的优点也是它的缺点,自然界中太多都是两态的,如何做到三种稳定的状态是个问题,原生的三进制比二进制每1位多一状态,也就说信息密度更大,同时算的也多,理论上讲会快1.6倍左右,能实现所使用的零件也会更少,但前提是能实现,反正现在没人实现。
2.1平衡三进制的模拟
因为硬件发展不起来,所以就不会有相应的系统与软件,就形成不了生态,简单来说,平衡三进制计算没戏,处非有研制硬件出来,而我又太想知道前苏联的三进制是怎样的,所以走了模拟一条路,虽然性能肯定不如原生的三进制计算机,但能先将它重现出来,后面如何优化,那就是后面的事了。
道家说“道生一,一生二,二生三,三生万物”,儒家有“三人为众”及“三人行必有我师”,可见“三” 在我国传统文化中有着崇高的地位,现在就是二生三,用二进制来模拟三进制,如果能跑起来就会有优化的空间,从而不断的叠代,就像一个观点,人工智能不管你用的是什么进制,它的关键是你用的是什么样的算法。
2.2平衡三进制的二进制转述
先看这有关三进制计算实现的一些猜想!,现在就是这样子弄;对于理论满分但从未实操过人来说,想在二进制的硬件上尽可能的高效的模拟平衡三进制,这就目前的最优法;虽然说弄出来的机器可能比原来的二进制效率还低,但是它能跑呀,如果硬件发展起来,那就可以替换,直接完成一波反超。
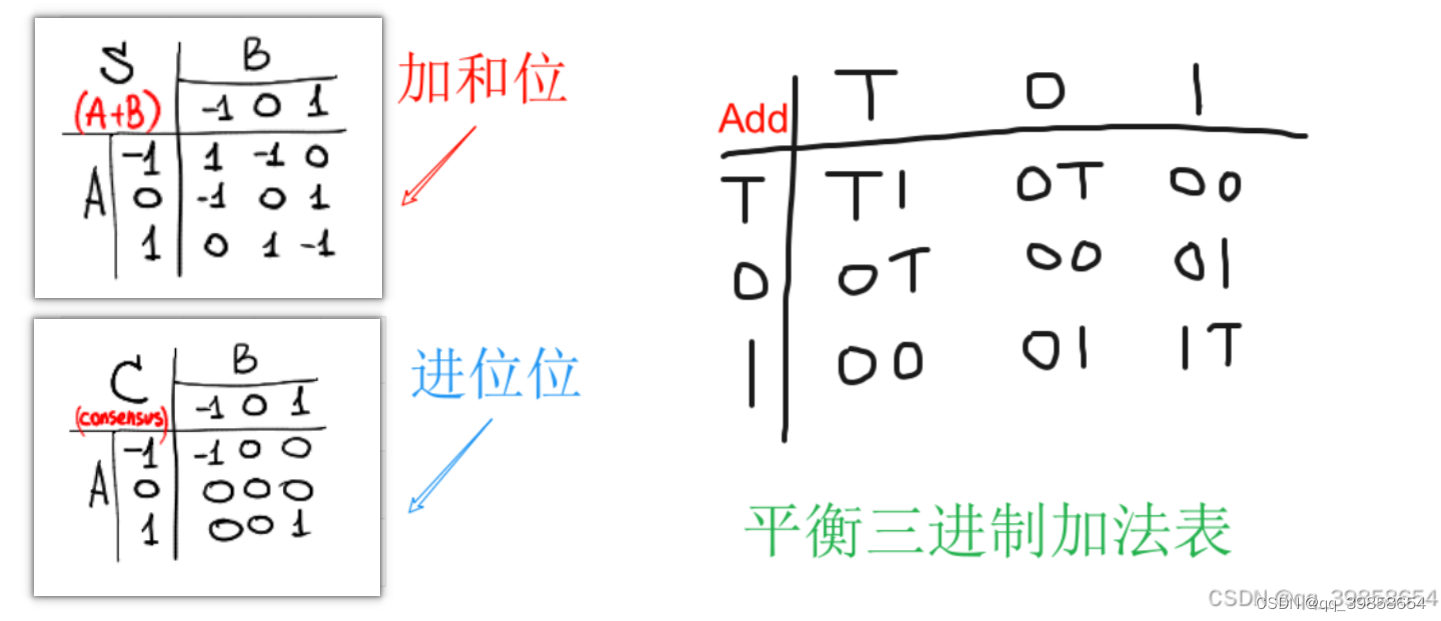
二进制的1位,称为bit,可以表示0或1,然后8个bit表示1个字节(byte);相应的平衡三进制也这样的设定,1位三进制位,称为trit,可以表示T(-1)、0、1,然后6个trit表示1个三进制字节tryte;要用二进制的数,模拟平衡三进制的1位三进制位,至少要用2bit,所以在本文中:2bit=1trit;这种方法是可以跑来的,我已经用这种方式在图灵游戏中成功构建出平衡三进制全加法器,就是下图这样子的:

2.3平衡三进制的二进制编码
使用的二进制编码为:T(00)、0(01或10)、11(11),这种方式的编码是我试了很多方案得到的最优解,这样的编码方式能极大的简化硬件的设计,对于0它为什么会有两个编码,最开始是不知道用那个好,图省事就放一起了,后面发现这两个放一起确实很好用,所以就固定一起了,平衡三进制最重要的一点就是对称,这就很平衡三进制了。
也可以用非位置化系统来解释,00得为0、01或10得为1、11得为2,刚好是0、1、2是标准三进制的表示,转成平衡三进制就是T、0、1,再看看这文章:有趣的平衡三进制!!!,看平衡三进制的逻辑门部分,用什么样的编码方式能最简化表示,很多次尝试下来,就是上面的编码方式,先看下图:

举个逻辑与为例子:
- 当T(00)与T(00)时,两个二进制的AND门,得到结果为T(00)
- 当T(00)与0(01)时,两个二进制的AND门,得到结果为T(00)
- 当T(00)与1(11)时,两个二进制的AND门,得到结果为T(00)
- 当0(01)与T(00)时,两个二进制的AND门,得到结果为T(00)
- 当0(01)与0(01)时,两个二进制的AND门,得到结果为0(01)
- 当0(01)与1(11)时,两个二进制的AND门,得到结果为0(01)
- 当1(11)与T(00)时,两个二进制的AND门,得到结果为T(00)
- 当1(11)与0(01)时,两个二进制的AND门,得到结果为0(01)
- 当1(11)与1(11)时,两个二进制的AND门,得到结果为1(11)
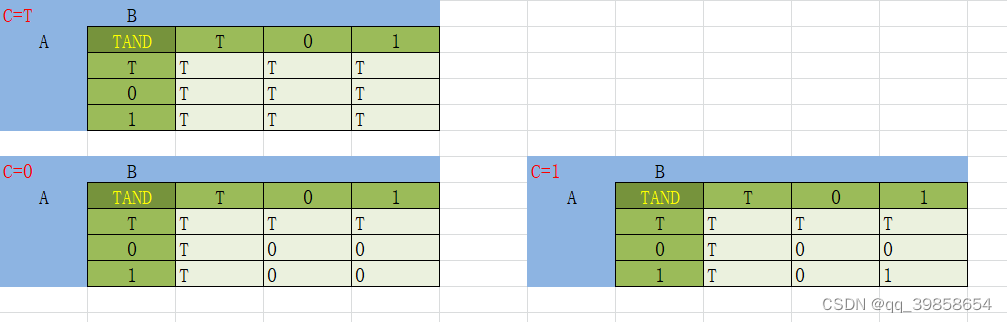
基本上没有问题了,但注意了0有两个编码,第五条,当0同时为01或10时,得到结果正确,但一个是01另一个是10,得到结果就是T(00)了,所以这种情况要单独处理,只要处理了0与0的情况,只一个或输出01或10即可,这样就得到了一个平衡三进制的与门了。
同样的用两个或门、两个或非门、两个与非门,同样可以得到剩下的三个表,非门也很简单就是每一位取反,T(00)取反得1(11)、1(11)取反得T(00)、0(01)取反得0(10),看0它有两个编码的好处就体现出来了,量子计算机有叠加态,那三进制计算的0有两个编码(状态)也是正常的,就像它的布尔值:FALSE(T)、UNKNOWN(0)、TRUE(1),T表示假,0表示“二者”,1表示真。
3、平衡三进制基础门的构建

先看上图,这个定律在二进制是管用的,也就是可以取反输入或输出就转换门的类型,然后我用上述二进制构建出来的平衡三进制门,也是管用的这没有想到吧,这是用二进制模拟的三进制,低层仍是二进制,但逻辑是平衡三进制,所以说原生的平衡三进制也是管用的,这个定律在平衡三进制上得到了扩展。
3.1平衡三进制逻辑与门

如上图所示,用上面的编码方式,只用了两个二进制的与门就完成电路的大部分逻辑的构建,其中的两个XOR与AND,是为了检测双0的输入情况,如果是双0输入则默认输出01,其它输出两个二进制的与门的结果。
3.1平衡三进制逻辑或门
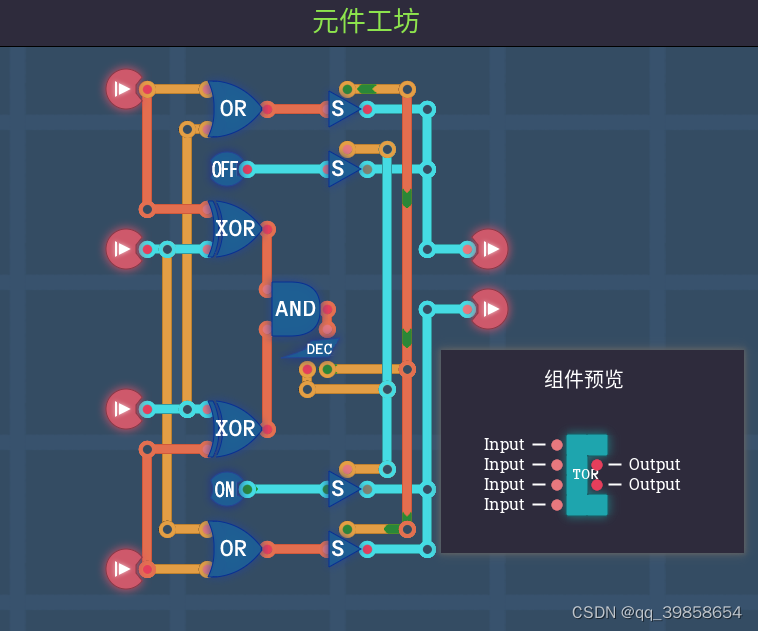
如上图所示,电路并没有大的改变,只是将两个二进制的与门,换成了两个二进制的或门,就是那么简单,得到了平衡三进制的的或门(TOR),剩下的TNOR(或非)、TNAND(与非)、TXOR(异或)、TXNOR(同或)同理可得。
3.3平衡三进制与非门、或非门
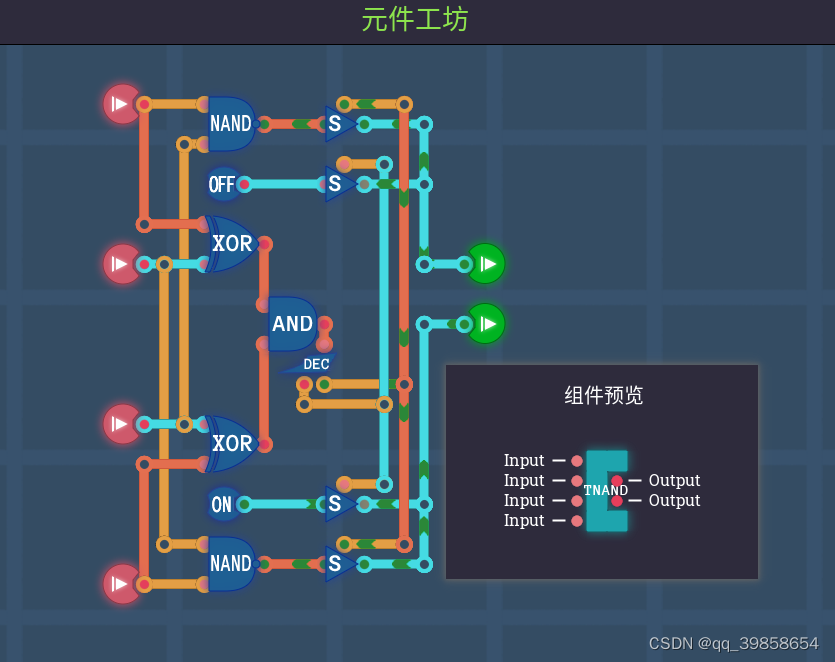
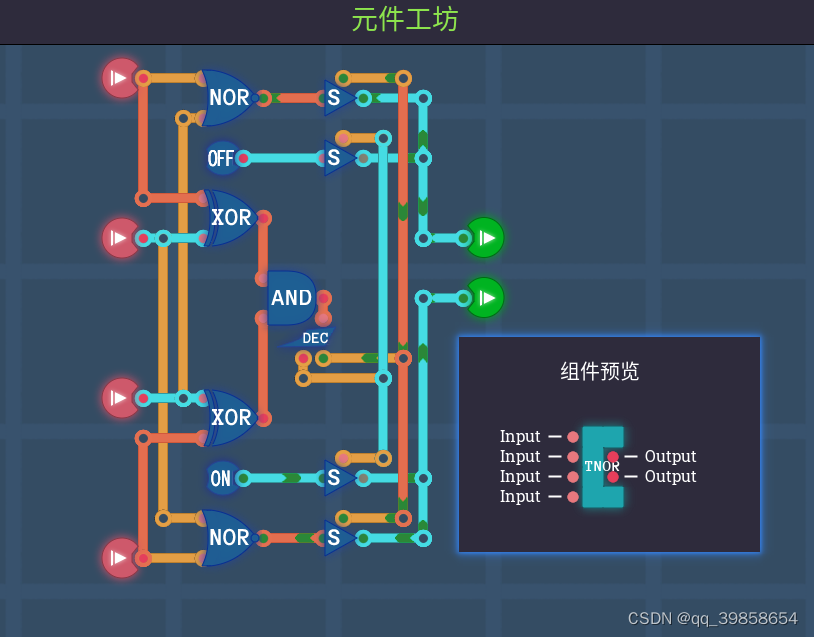
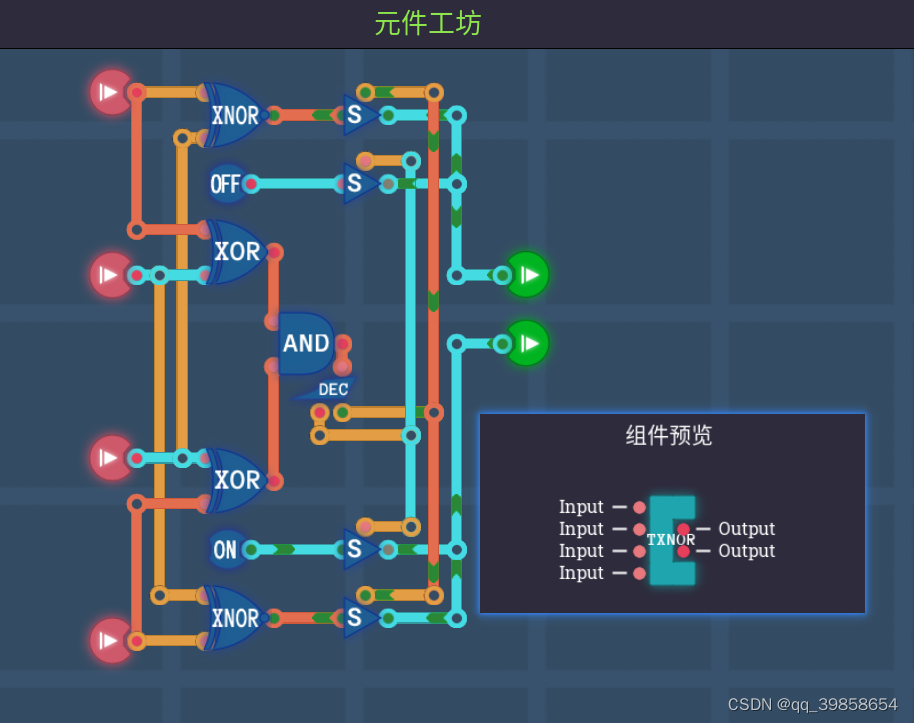
3.4平衡三进制异或门、同或门

3.5平衡三进制摩根定律的应用
元件工坊构建出的平衡三进制础门,它们的真值表是对称的,这四个基础逻辑门分别是:TOR、TNOR、TNAND、TAND,你可以通过如下图所示的对输入取反(垂直箭头)或对输出取反(水平箭头)来转换它们。
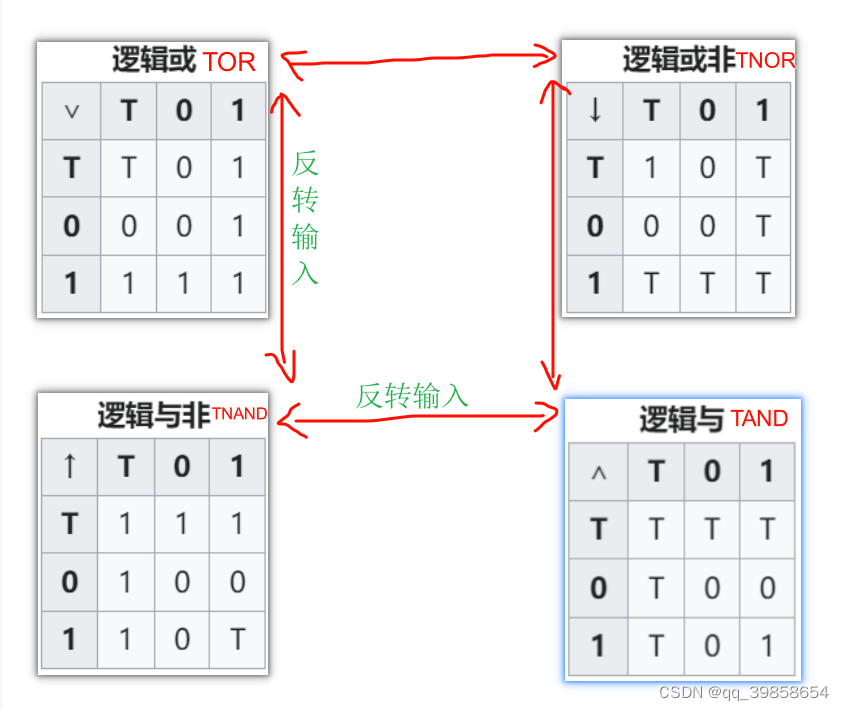
先看它的取反,也就是T变1、1变T、0不变,用上述的编码方案,只要分别对每一位取反,即可得平衡三进制的非门,如下图所示:

也就是说,当它为TOR组件时,想变为TNAND组件,分别对它的两个输入,用TNOT组件取反,就得到了TNAND级件,如果对输出结果再取反,就变成了TAND组件,从或门变成了非门;同样的TXOR,对输出结果取反,就得到了TXNOR组件。
4、平衡三进制基础门构建2
4.1平衡三进制三与门
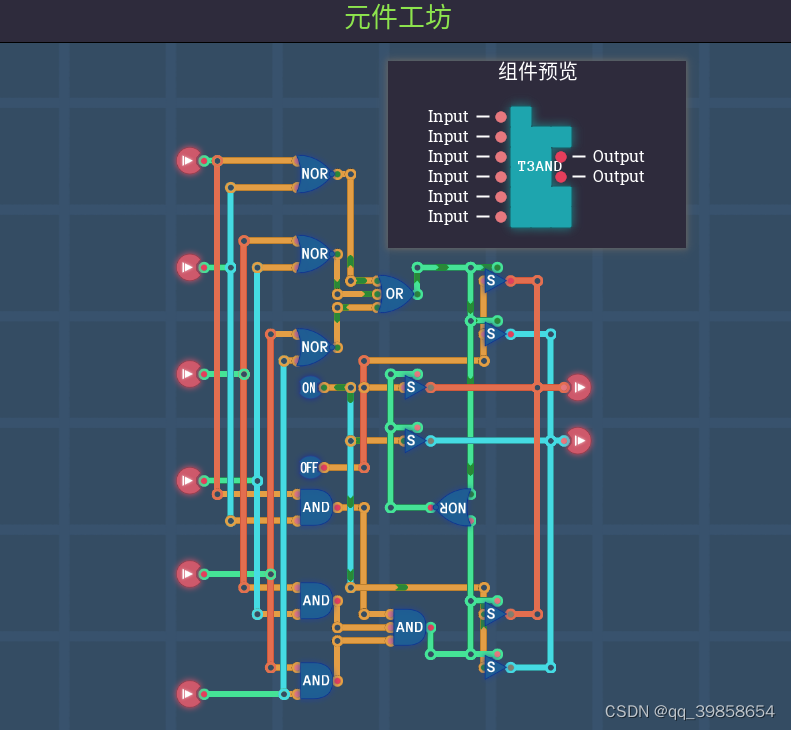
如上图所示,这个部件是将三个trit进行与操作;二进制的与门(两个才是真,一假则全假),平衡三进制的与门可以看上面的真值表,它也是类似,TAND它是如果一个输入为T则出T,两个输入为1则出1,其余都出0;然后先用两个平衡三进制与门得到结果,再用这个结果与第三个与门就可以得出结果;所以上述的部件分别判断了是否输入中有T、是否输入全为1、及其余情况的0,这样就可以得到平衡三进制的三与门了。
4.2平衡三进制三或门

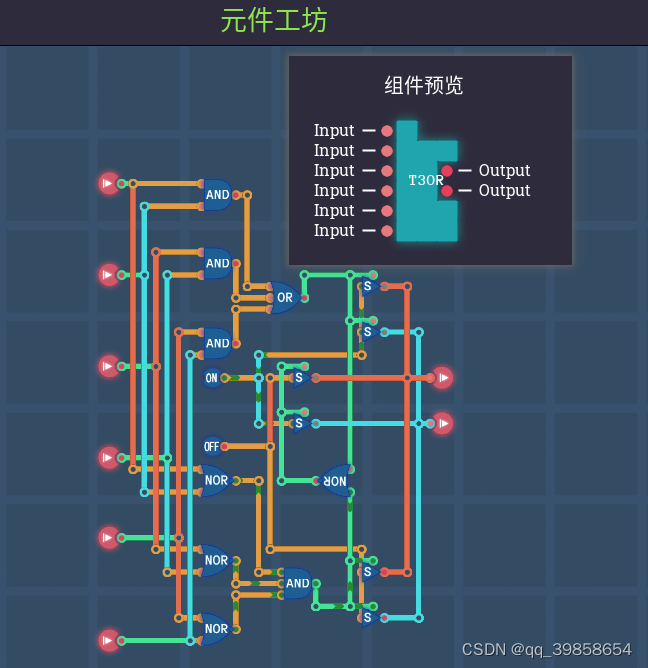
如上图所示,这个部件是将三个trit进行或操作;与上面的方法类似,结合真值表,其中任意一个输入为1则出1,若三个输入都为T则出T,其它出0,这样就可以得到平衡三进制的三或门了。
4.3平衡三进制三态复用器
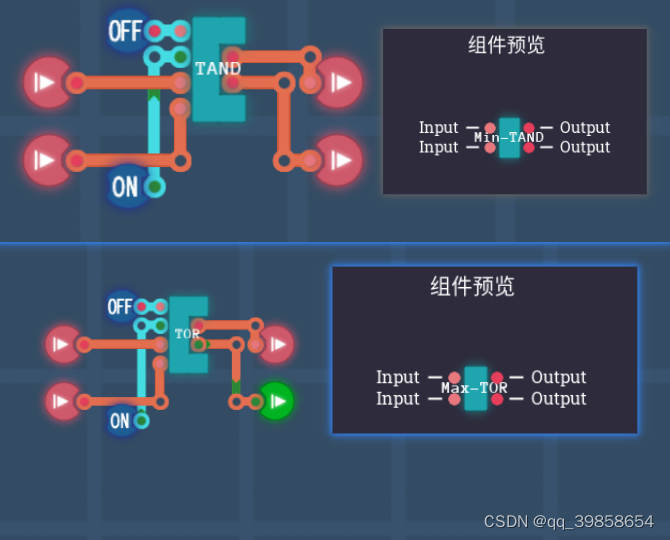
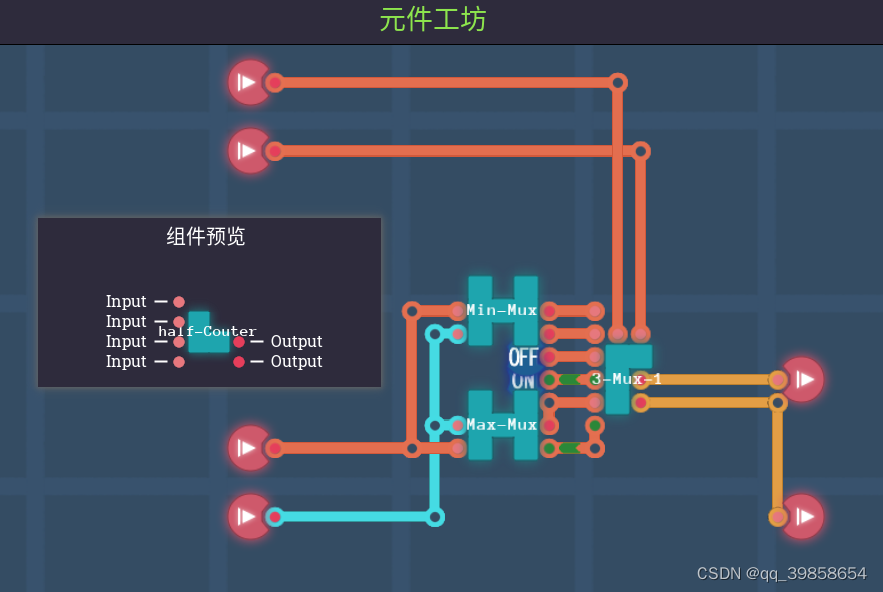
全称三态多路复用器,当我们要用解码或加法器时,就要用到它,也就是三选一,这里有T(00)、0(01或10)、1(11),在平衡三进制全加器中有详细讲到,按照这思路就可以三选1的电路,那一亮就是那一路的数据,如下图所示:
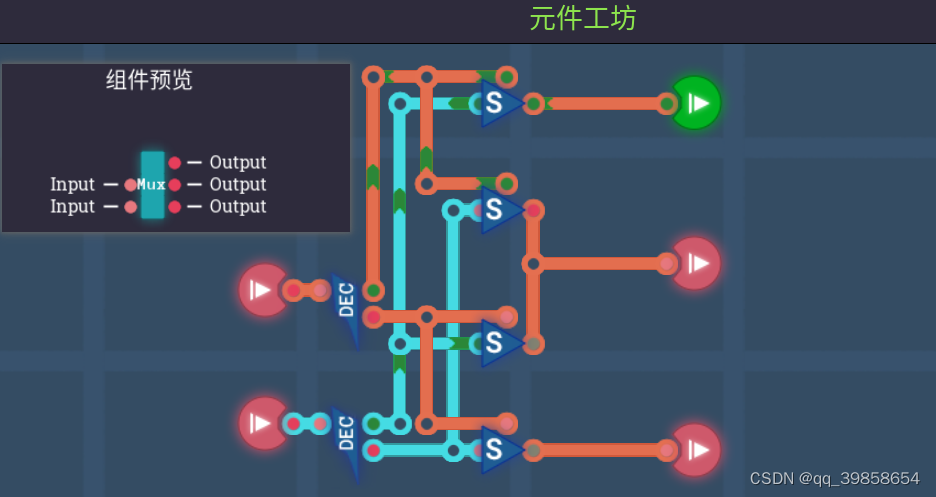

可以看上面的两个图,都是三选1基础件,这个基础件的作用就是:输入00第一路亮绿灯,其它路红灯;输入01或10第二路亮绿灯,其它路红灯;输入11第三路亮绿灯,其它路红灯;这样再加上六个通路切换嚣,就可以构建出一个三态多路复用器,可以作为加法器的基础了,如下图所示:
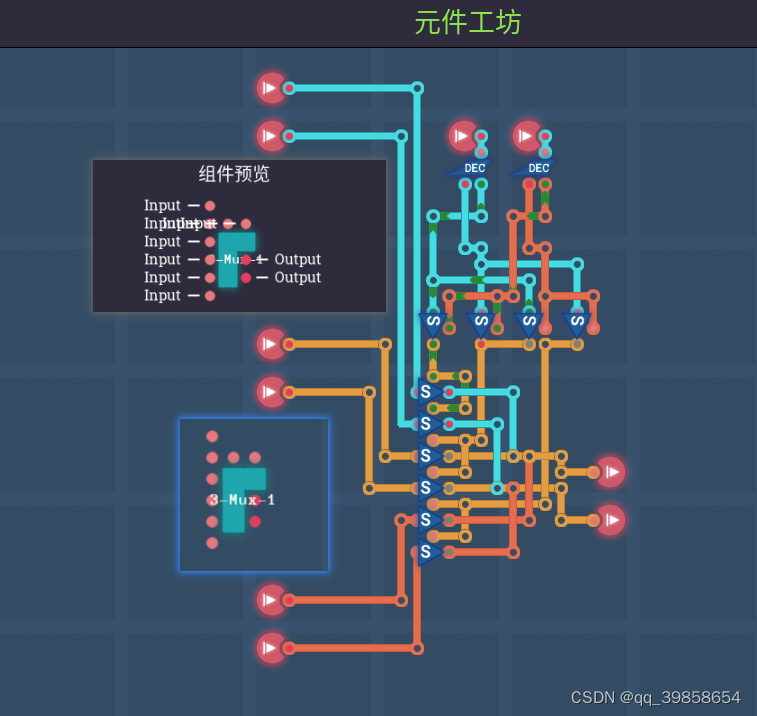
这样就有三选1数据选择器了,看过平衡三进制加法器文章的,这个就是三态多路复用器;当输入T/0/1时,数据从第1/2/3路输出,因为2位bit代表1trit,所以它有10个引脚;有了这组件,平衡三进制的全加器也可以弄出来了,二进制的加法器方案放这里不管用,所以要上述的的平衡三进制加法器文章中的加法器。
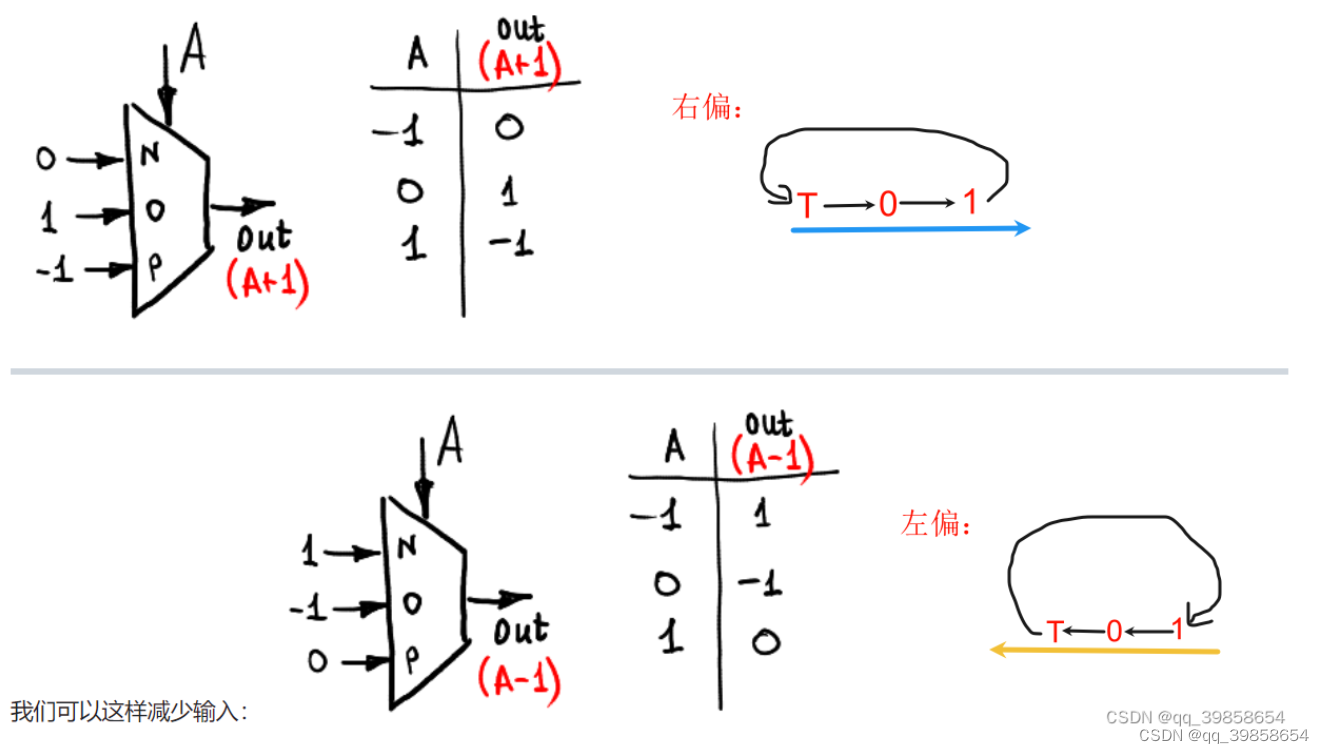
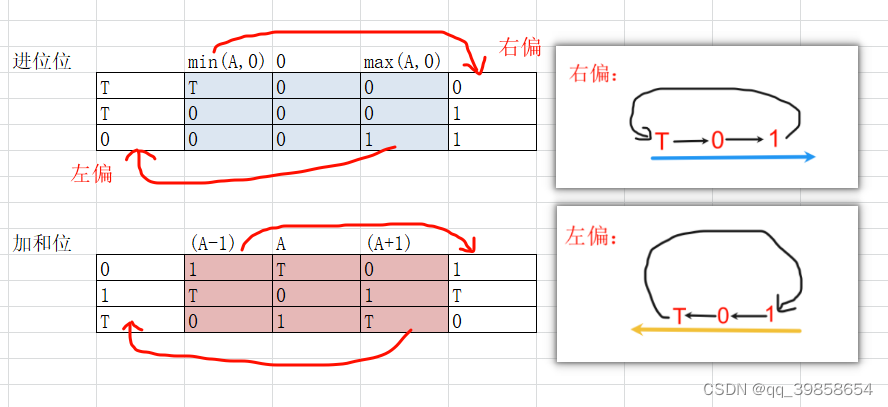
4.4平衡三进制左偏门、右偏门
这里的左偏与右偏门在全加器有用到,所以现在弄成一个基础件,它可以转换输入,从而简化输入,例如右偏:当输入T时,输出0;当输入0时,输出1;当输入1时,输出T;下面就是它的输入与输出真值表。
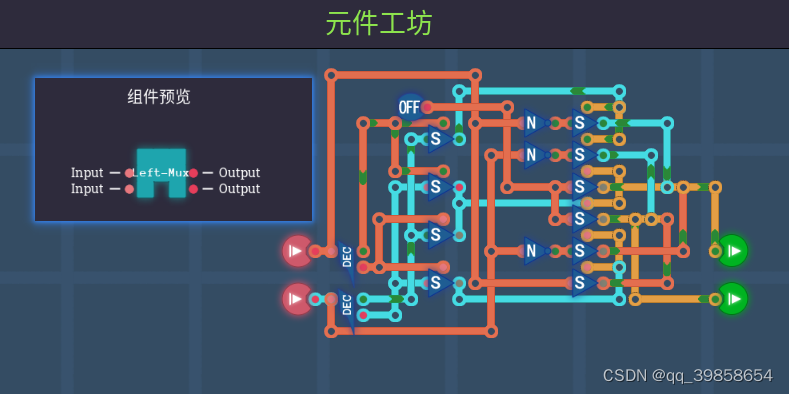
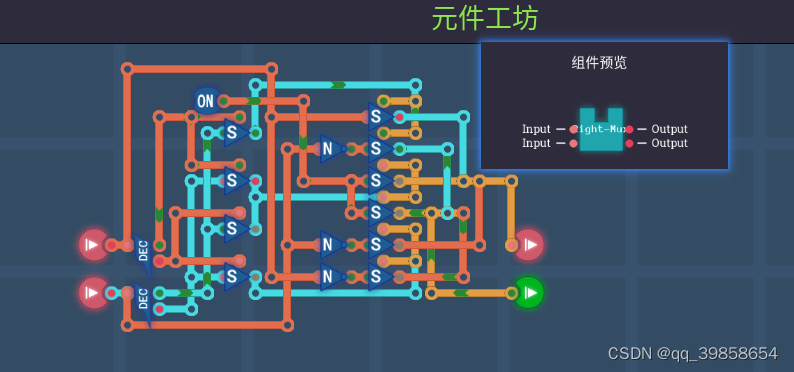
如上图所示,平衡三进制左右偏门都用到了前面的三选1基础件1,当然也可以用三选1基础件2,效果一样,这样确实是零件多了,但是确实也是简化了输入。
4.5平衡三进制最小门、最大门
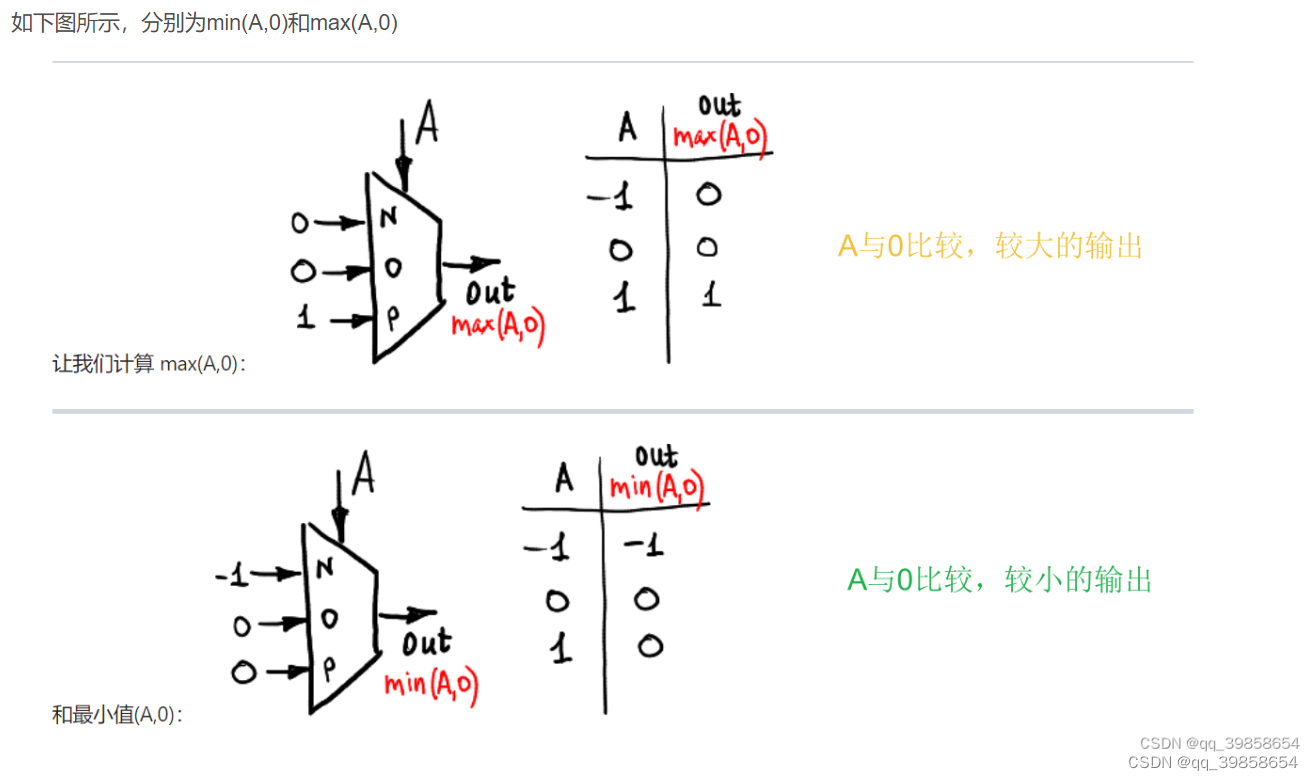
如上图所示,在平衡三进制全加器中,还用到了最大门与最小门,它的构建可以用类似于左偏门和右偏门的方法,这样也就形成了Max(A,0)与Min(A,0),如下图所示:

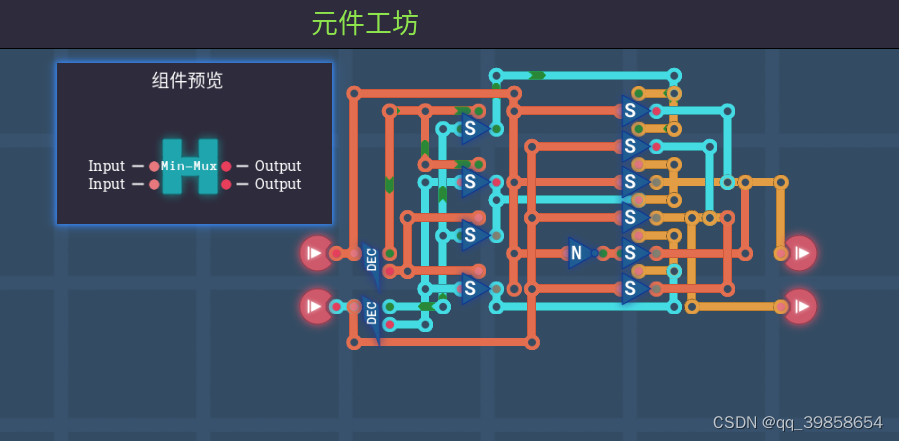
说完了Max(A,0)与Min(A,0),其实平衡三进制与门和或或门,最可以当做逻辑最大门及逻辑最小门,它其实是从不同角度来解释的,思路与下面的截图来自于文章三生万物,请看下图:
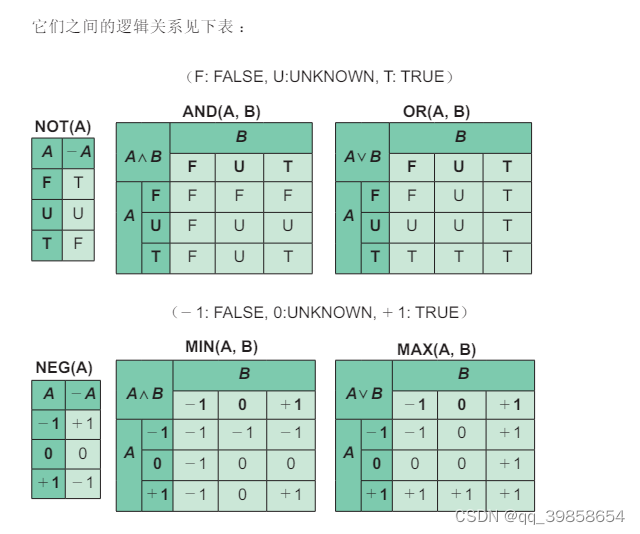
在这我们要明确一点,逻辑是逻辑,数值是数值,明白这一点很重要; 当从逻辑上去想,那么T表示假,0表示两都,1表示真,那么得到的就是平衡进制的与门及或或门; 当从数值上去想,那么T表示-1,0表示0,1表示1,那么得到的就是平衡进制的最小门及或或门,也就是与门成为了Min(A,B)及或门成为了Max(A,B),也就是说这两个门可以比较大小,输出最大或最小值,同样也可以用来构建Max(A,0)与Min(A,0),如下图所示:
这样最后得到的设计,就非常简便了,而且用这个Min(A,B)门及Max(A,B)门,也就是与门及或门,可以制作一个对比数字大小的电路,对比两个数的大小有:0与0、正数与负数、0与负数、0与正数、正数与正数、负数与负数,总共6种情况,从最高位左起第一位若非 0 值,就可判断它的正负性,是 T 即为负数,是 1 即为正数。
这样就可以解决:0与0、正数与负数、0与负数、0与正数,这些情况的判断了,剩下的双正与双负的判断,可以先在前面补0让两个数对齐,然后从最高位开始,依次对比每一位大小,相同时跳过进行下一位,只要路径中有一位大于另一位则出结果,不然全部对比完都相同,则两都数都是相同的。
5、平衡三进制加法器
在前面平衡三进制全加器,我们已经给出它的真值表及设计图,现在就可以实现它了,它需要左偏门(A-1)、右偏门(A+1)、最大门Min(A,0)、最小门Max(A,0)门、三态复用器3Mux1,按照下面的思路就可以弄出来了。
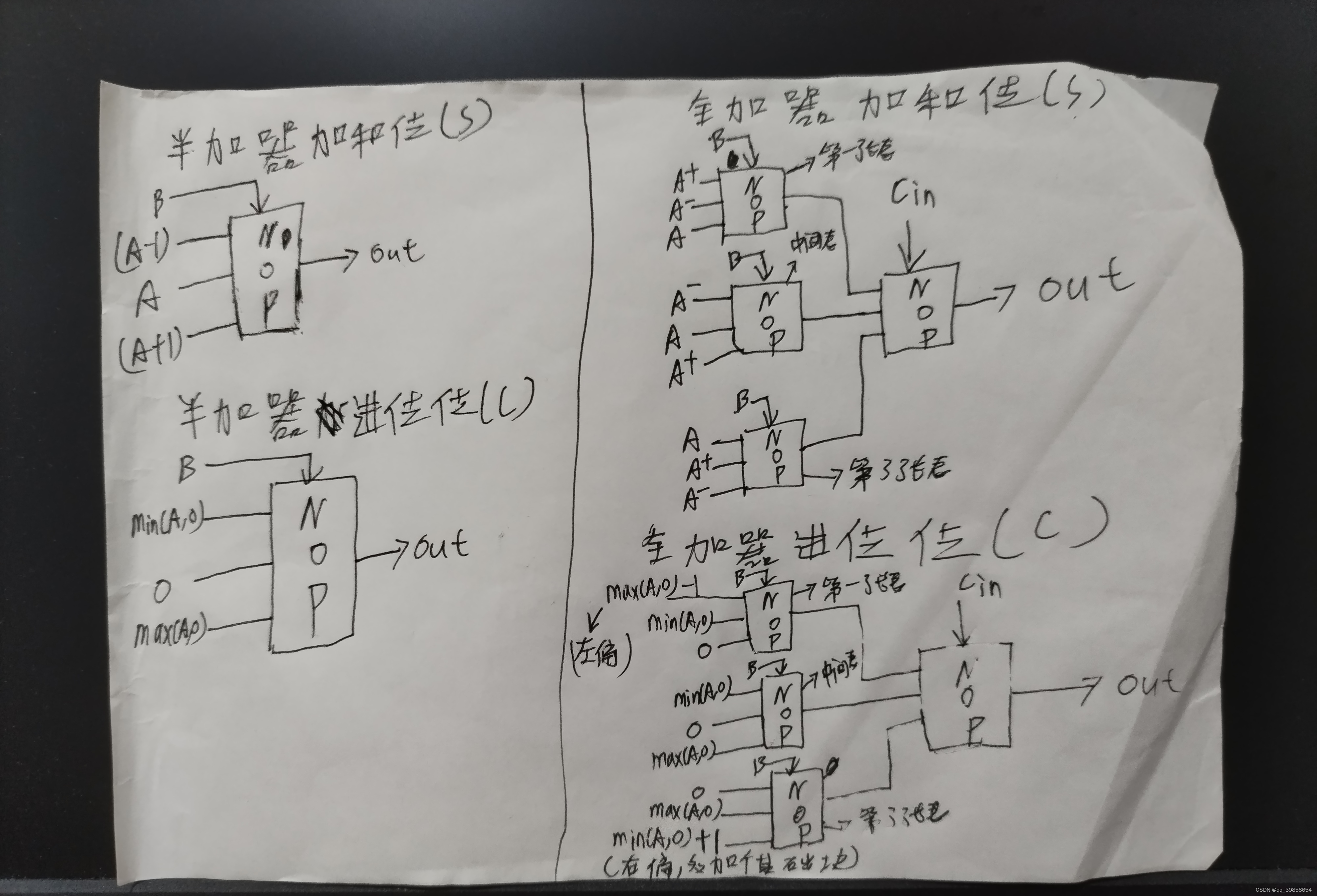
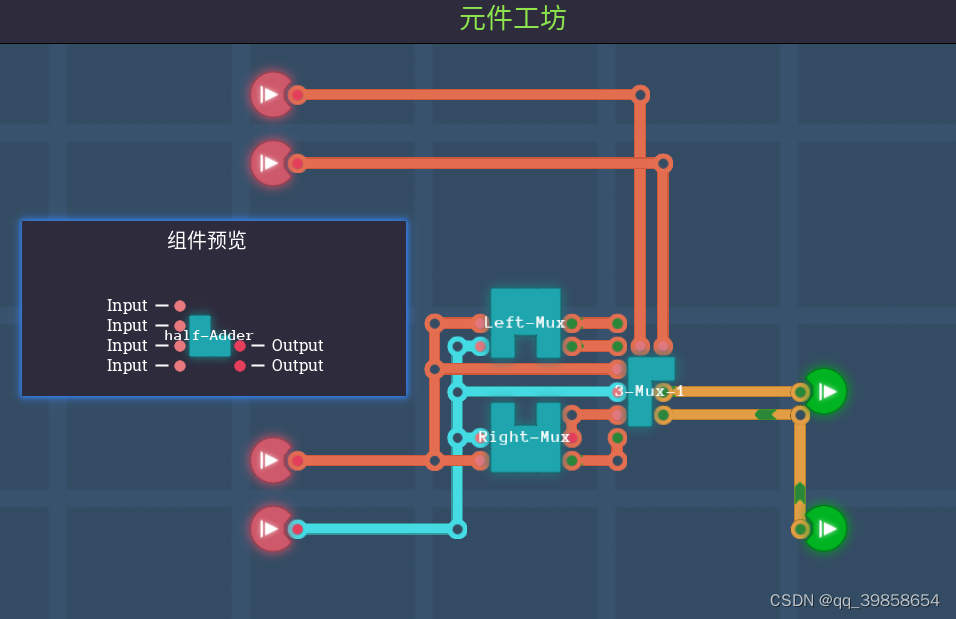
5.1平衡三进制半加器
如上图所示,半加器的真值表,它的电路分为加和位与进位位,其实它的输入用了左偏与右偏及Max(A,0)与Min(A,0),这样是简化了设计思路,但加了零件成本,后期可以单独增加两条线路,专门用于不同的输入,可以得到下面两张图:
5.2平衡三进制全加器
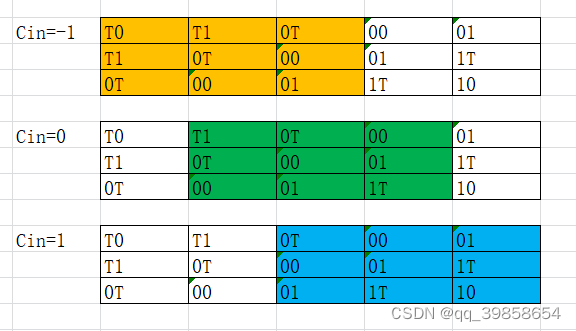
只要其中一张就可以表示所有的输出结果了,这样将它的加法位与进位位分开,就得了它的输入逻辑了,如下图所示:
这样就可以完成设计了,也就是下图所示:

如上图所示,有6个输入,最上面的2个输入代表进位位,后面的4个输入代表,可以输入两个平衡三进制数;有4个输出,上面是加和位,下面是进位位,跟二进制的加法器很想,但只是每一位trit都要2bit来表示,经过测试这个电路完全符合预期的标准,对加位的电路做了优化,也就是将输出的结果进行了左偏与右偏,再用第三位做选择,就可以少用一些电路,但对于进位位,它不能这样做,因为它偏置操作也得不到想要的数据,所以用偏置后错误的数据,再用第三位选择也得不到正确的结果。
5.3平衡三进制多位加法器
为什么是4位加法器,在二进制中1byte=8bit,在这里用2bit代表1trit,所以只能1byte=4trit,和前苏联的三进制计算机相比,还少了2trit,标准的是6个trit=1个三进制字节tryte;如果想达到标准的6个trit,那需要12bit才行,图灵完备只有8bit,所以只能弄4trit的平衡三进制加法器了;二进制的8位全加器串联可计算255以内的加法,也就是2个byte输入及1个进位输入,输出是1个byte输出及1个进位输出,所以设计也要类似就行,如下图所示:
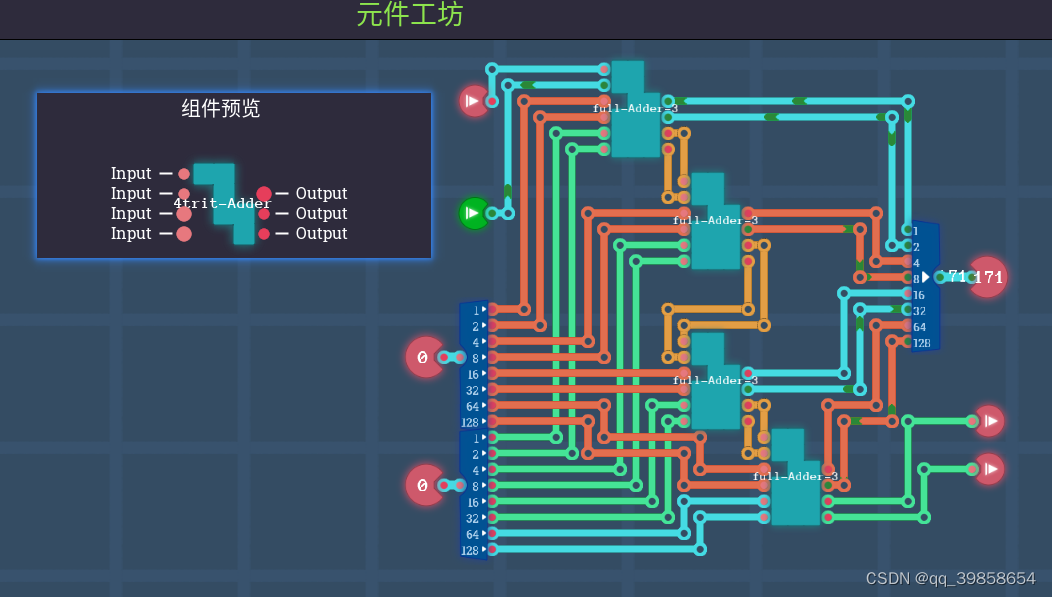
这就是类似于二进制的平衡三进制加法器了,它可以计算(-81到81)以内的加减法,是的,加减法,这个就是它的优点,加法器与减法器都是它,现在就可以试试它的计算功能了,如下图所示:


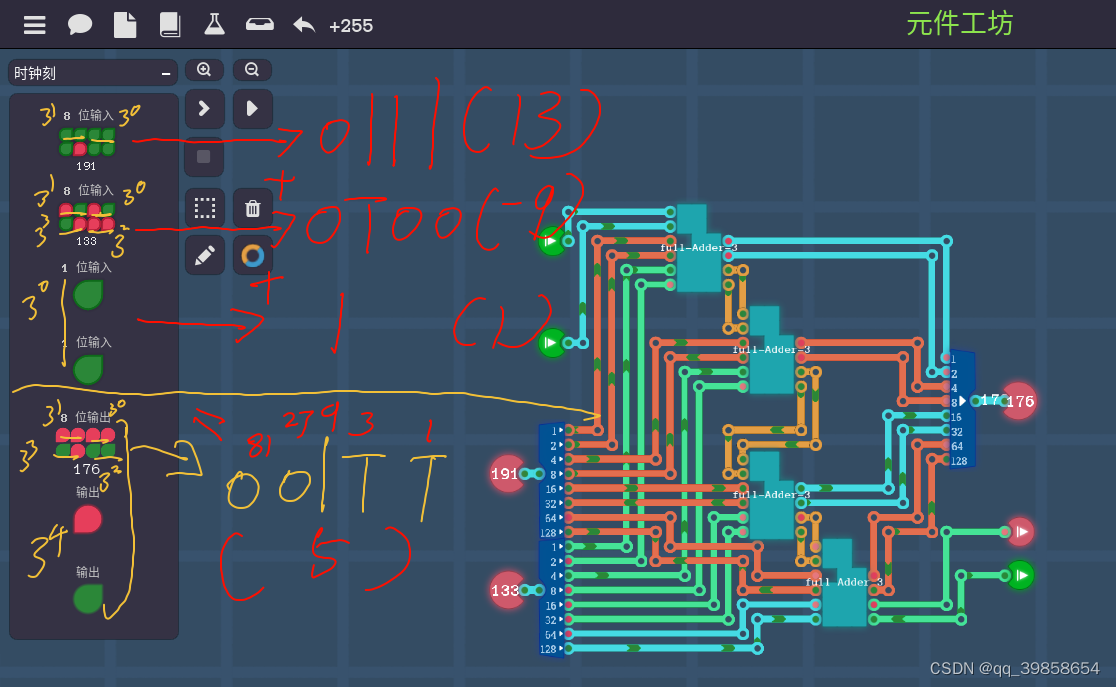
看完了上面,是否感觉,算的太少了,那就再串联一次,这样就得到了8trit的平衡三进制加法器了,下面的8trit加法可以算(-6561~6561)内的加减法,如果还不够可以继续串联,如下图所示的方法:

累了,更不动了,后面有空再更吧。。。
这篇关于《全网首发》平衡三进制图灵机的构建的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



