贪心的经典算法讲课笔记

本文主要是介绍贪心的经典算法讲课笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

贪心的经典算法

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所作出的是在某种意义上的局部最优解。

贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须是具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前的状态有关。

贪心算法具有最优子问题的结构，它的特点是“短视”，每次选择当前局面最有利的决策，来一步步获得最优解。 ——贪心算法概述

上面画出来的粗体字都是很关键的东西。

你们肯定都学过最短路径的贪心算法，我们来看一个Dijkstra算法例子：

很显然，如果从A出发到C，在选择的过程中，我们不能只看当前的状态。如果只看当前状态，选择的最短路就会是A->b->c，显然，这是错的。

所以一般对于一个问题来说，我们只讲这样一个贪心算法是错误的，而不说这个问题不能采用贪心算法——因为可能从别的角度设计出的贪心算法是正确。

基本的算法中贪心著名的贪心算法包括:

Dijskstr单源图最短路径算法
Prim和Kruskal最小生成树算法
Huffman编码简单压缩算法等。

可见贪心算法是比较“短视”的。而动态规划算法是从所有能达到当前状态的状态和决策中选取，所以从某种角度上讲，动态规划是枚举——比较优美的暴力

贪心和动态规划算法的比较：

-	贪心	动态规划
决策	最优的一个决策	枚举状态、决策
最优子问题	有	有
子问题重叠	一般没有	一般有
复杂度	一般低	一般高
正确性	需要数学证明	因为枚举，所以显然

接下来我们来学一学贪心算法。

Prim算法

最小生成树的Prim算法是贪心算法的一大经典应用。Prim算法的特点是时刻维护一棵树，算法不断加边，加的过程始终是一棵树。
一条边一条边的加，维护一棵树。
初始 ${ } E=\{\}$ 空集合， $V=\{任意节点\}$
循环 $(n - 1)$ 次，每次选择一条边 $(v 1, v 2)$ ,满足： $v 1$ 属于 $V$ ， $v 2$ 不属于 $V$ 。且 $(v 1, v 2)$ 权值最小。
$E = E + (v 1, v 2)$
$V = V + v 2$
最终E中的边是一棵最小

现在以下面的例子来讲解以下Prime算法

Prim算法的过程从A开始 V = {A}, E = {}

在这里插入图片描述
选中边AF , V = {A, F}, E = {(A,F)}

在这里插入图片描述
选中边FB, V = {A, F, B}, E = {(A,F), (F,B)}

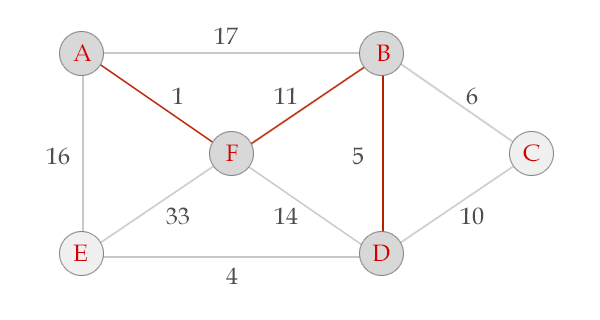
在这里插入图片描述
选中边BD, V = {A, B, F, D}, E = {(A,F), (F,B), (B,D)}

在这里插入图片描述
选中边DE, V = {A, B, F, D, E}, E = {(A,F), (F,B), (B,D), (D,E)}

在这里插入图片描述
选中边BC, V = {A, B, F, D, E, c}, E = {(A,F), (F,B), (B,D), (D,E), (B,C)}, 算法结束。
现在我来提供输入输出数据，然后写一个程序，来实现一下上面的过程

输入

第1行：2个数N,M中间用空格分隔，N为点的数量，M为边的数量。（2 <= N <= 1000, 1 <= M <= 50000)
第2 - M + 1行：每行3个数S E W，分别表示M条边的2个顶点及权值。(1 <= S, E <= N，1 <= W <= 10000)

输出

输出最小生成树的所有边的权值之和。

样例输入

6 10
1 2 17
1 6 1
1 5 16
6 2 11
6 5 33
6 4 14
5 4 4
2 3 6
4 3 10
2 4 5

样例输出

27

如果这个图要用邻接矩阵来存的话，内容是这个样子的

-	1	2	3	4	5	6
1		17			16	1
2	17		6	5		11
3		6		10
4		5	10		4	14
5	16			4		33
6	1	11		14	33

有兴趣的话，可以把上面的例子用自己的方法写一下，如果写不出来，我用下面的这个例题，来讲解一下最短路

题目：Jungle Roads
题目描述

这是一个修建道路的问题，题目会给你两个点，以及两个点之间的修路所花的钱。目标是使所有的点连通，且花费的钱最少，输出最少的钱。

输入描述

3 ：代表有3个点
A 2 B 10 C 40 ：A这个点与2个点相连，分别是B和C之间的花费对应10，40
B 1 C 20

Prime代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int INF = 0x3f3f3f3f;
int G[30][30];
int dis[30];
bool vis[30];
void init()
{memset(G,INF,sizeof(G));memset(dis,INF,sizeof(dis));memset(vis,0,sizeof(vis));
}
int main()
{int n,m,w;char u,v;while(cin>>n && n){init();//初始化for(int i = 0; i < n-1; i++)//存图的过程{cin>>u>>m;while(m--){cin>>v>>w;G[u-'A'][v-'A'] = w;G[v-'A'][u-'A'] = w;}}//Prime算法dis[0] = 0;//把第一个点初始化为0int ans = 0;for(int i = 0; i < n; i++){int pos = -1;for(int j = 0; j < n; j++)//找当前最小值{if(!vis[j] && (pos == -1 || dis[pos] > dis[j])){pos = j;}}ans += dis[pos];vis[pos] = true;for(int j = 0; j < n; j++)//更新dis数组{if(!vis[j] && dis[j] > G[pos][j]){dis[j] = G[pos][j];}}}cout << ans << endl;}return 0;
}

Kruskal

kruskal和并查集的代码一样，先学一下并查集，这个直接就会了

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 30;
struct edge
{int u,v,w;
}edges[maxn * maxn];
int f[maxn];
int cnt = 0;
void addedge(int u, int v, int w)
{edges[cnt].u = u;edges[cnt].v = v;edges[cnt].w = w;cnt++;
}
int Find(int x)
{if(x == f[x]) return x;f[x] = Find(f[x]);return f[x];
}
int Kruskal()
{int ans = 0;for(int i = 0; i < cnt; i++){int r1 = Find(edges[i].u);int r2 = Find(edges[i].v);if(r1 != r2){f[r1] = r2;ans += edges[i].w;}}return ans;
}
bool cmp(struct edge a, struct edge b)
{return a.w < b.w;
}
void init()
{cnt = 0;for(int i = 0; i < maxn; i++){f[i] = i;}
}
int main()
{int n,m,w;char u,v;while(cin>>n && n){init();for(int i = 0; i < n - 1; i++){cin>>u>>m;while(m--){cin>>v>>w;addedge(u-'A',v-'A',w);addedge(v-'A',u-'A',w);}}sort(edges,edges+cnt,cmp);cout << Kruskal() << endl;}
}