二叉树操作 递归与非递归实现

本文主要是介绍二叉树操作 递归与非递归实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

 

采用递归的方式创建如下二叉树；

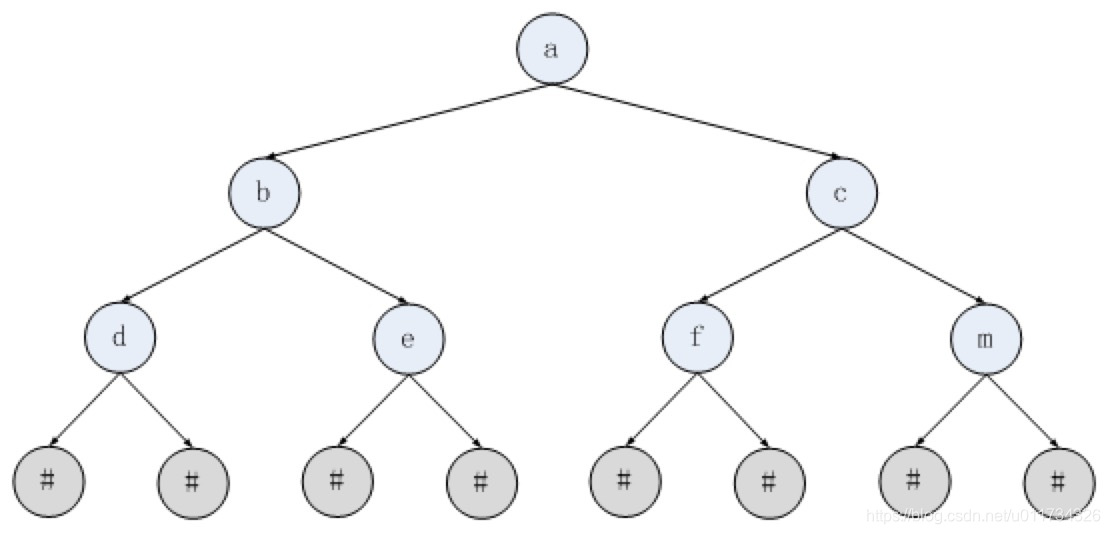
    输入'#'代表当前子树结束。

 

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef struct btn
{struct btn * lchild, *rchild;char data;
}btree, *BT;//递归创建二叉树
void createTree(BT * b)
{char ch;scanf("%c",&ch);getchar();//printf("--:%c\n",ch);if(ch == '#'){*b = NULL;return;}else{*b = malloc(sizeof(btree));(*b)->data = ch;createTree(&((*b)->lchild));createTree(&((*b)->rchild));}return;
}//前序 递归遍历(根左右)
void preOrderTraverse( btree * root)
{if( root == NULL)return;printf("%c ", root->data);preOrderTraverse( root->lchild);preOrderTraverse( root->rchild);
}//中序 递归遍历(左根右)
void inOrderTraverse( btree * root)
{if( root == NULL)return;inOrderTraverse(root->lchild);printf("%c ", root->data);inOrderTraverse(root->rchild);
}// 后序 递归遍历(左右根)
void postOrderTraverse(btree * root)
{if( root == NULL)return;postOrderTraverse(root->lchild);postOrderTraverse(root->rchild);printf("%c ",root->data);
}//前序 非递归遍历
void preOrder_without_recursion(btree * root)
{BT stack[100];BT p;int top = 0;p = root;while( p!= NULL || top != 0){while(p!=NULL){printf("%c ", p->data);//先打印当前子树的根节点stack[top++] = p;//将根节点入栈p = p->lchild;// 操作左子树， 重复以上两步}p = stack[--top];//出栈p = p->rchild;// 操作右子树}
}//中序 非递归遍历
void inOrder_without_recursion(btree * root)
{BT stack[100];BT p;int top = 0;p = root;while( p!= NULL || top != 0){while(p!=NULL){stack[top++] = p;p = p->lchild;}p = stack[--top];printf("%c ", p->data);p = p->rchild;}
}//后序 非递归遍历 （左右根）
void postOrder_without_recursion(btree * root)
{BT stack[100];BT p;int top = 0;p = root;while( p!= NULL || top != 0){while(p!=NULL){stack[top++] = p;p = p->lchild;}//打印节点需要满足以下两个条件中的任一个：//    1. 如果当前操作节点p是其父节点的右孩子//    2. 如果当前操作节点p是其父节点的左孩子，且父节点右孩子为NULLwhile( p == stack[top-1]->rchild || (p == stack[top-1]->lchild && stack[top-1]->rchild == NULL)){p = stack[--top];printf("%c ", p->data);if(top == 0)return;}p = stack[top-1]->rchild;}
}int main()
{	btree * head  = NULL;printf("create btree:\n");createTree(&head);printf("\n\n");printf("preorder: ");preOrderTraverse(head);printf("\npreorder without recursion:");preOrder_without_recursion(head);printf("\ninorder:  ");inOrderTraverse(head);printf("\ninorder without recursion:");inOrder_without_recursion(head);printf("\npostorder:");postOrderTraverse(head);printf("\npostorder without recursion:");postOrder_without_recursion(head);	printf("\n");
}

运行结果：

randolph@ubuntu:~/test$ ./a.out 
create btree:
a
b
d
#
#
e
#
#
c
f
#
#
m
#
#

preorder: a b d e c f m 
preorder without recursion:a b d e c f m 
inorder:  d b e a f c m 
inorder without recursion:d b e a f c m 
postorder:d e b f m c a 
postorder without recursion:d e b f m c a 
 

注意：

     整个过程中最难理解的是二叉树的后续非递归遍历， 二叉树的后序遍历顺序为，root->lchild, root->rchild, root，非递归遍历的难点是怎么从root->rchild转换到root， 所以我们打印节点的条件是先将左子树遍历完毕，然后满足下面的条件
        1. 如果当前操作节点p是其父节点的右孩子
        2. 如果当前操作节点p是其父节点的左孩子，且父节点右孩子为NULL

 

 

这篇关于二叉树操作 递归与非递归实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---