本文主要是介绍深入浅出談 隐马尔可夫的概念(1/ 2),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、说明
- 二、Markov Chain
- 三、Introduction
- 四、State Sequence
- 五、Comment
- 六、介绍隐藏式马可夫法则。
- 七、隐藏马尔可夫Introduction
- 八、结论
一、说明
在许多机器学习的章节中,常常遇见 HMM ,往往看到它的数学式子后,就当没看到似的跳过去了,其实它的基础理论并不难,尤其是 Markov Chain 在高中数学课本就已经出现过了,但…那么久远的事,相信大家都忘得差不多了,现在一起来回顾一下吧!!
二、Markov Chain
在状态空间中,了解当前的状态与下一个状态发生的随机过程。
(疴…有讲等于没讲,来看一下 Key point 吧! )
Key point:
如左下图,现有三间大型卖场在AIA附近,分别是Costco、爱买、大润发,已知顾客今日在各个卖场间流动的固定几率(invariant),亦即图上的数字,值得注意的是,从每间卖场画出去箭头上的数字相加起来为1 (ex: Costco 0.7+0.2+1 = 1)。 接着来看一下范例吧…
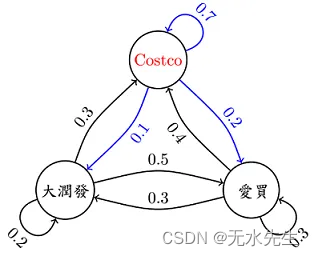
今天刚来AIA报到的学员圆仔,看到卖场广告后,会到三间卖场的机率分别为0.5、0.1、0.4,那么上课第三天圆仔会到Costco逛的机率是多少? (解法如下)


三、Introduction
透过上述例子可以知道,当前的状态跟上一个状态有关,是不是有些感觉了咧? 接下来,就跟着一起走进数学的世界吧!!!
符号介绍:
•假设有 N 个状态,分别标示为 s₁, s₂, …, s_N
•假设从当前状态 si 变成 sj 的机率为 aij,可表示成转移矩阵(Transition Matrix) A,如下…

•我们纪录第 t 秒的状态在第 i 个状态为 qt = i
•起始时间选定某个状态 si 的机率为 πi ,又可标为 P(q₀ = j)
四、State Sequence
一开始我们会选定一个起状态,然后每过一个单位时间,就会选择走过某一条与当下状态相关的边,到达下一个状态,经过 T 秒后,我们就会得到一条有 T 条边、 T+1 个状态的有序路径(亦称之,state sequence)。
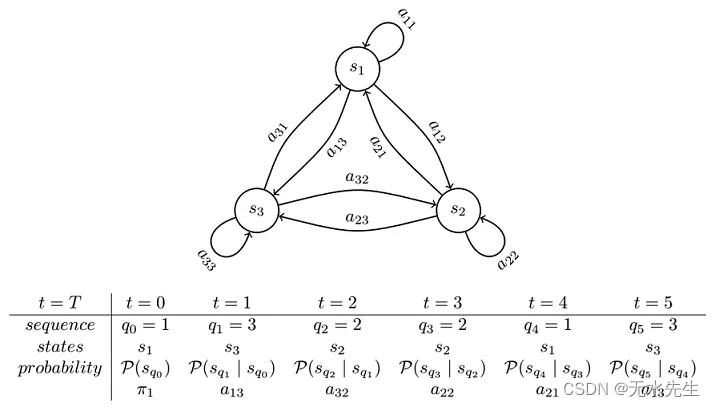
如果上述说的实在抽象,我们用3个状态、5个时间单位说明吧! 如左图和表格,我们经过5个时间点,会得到6个状态的一条路径,因此我们可以算得形成这条路径的机率是多少?
机率 = π₁ a₁₃ a₃₂ a₂₂ a₂₁ a₁₃
上述的例子,应该可以让大家比较有深刻的感触吧! 不免俗的,还是用数学式子写一下…在有 T 个时间单位下…我们会得到 state sequence Q
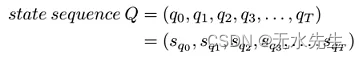
最后,可以得到 Q 的机率为

五、Comment
在固定状态转换 (invariant)的机率下,一切如上述,似乎单纯,如果我们再加入一些变动因素,举两个常见的例子来看看啦!
(1)学员圆仔每日到卖场的机率,会加入他当日出差路线而有异动,即是与时间相关的非固定状态 (time variant)啦! 其实也没那么复杂,底下的图,让你秒懂这一切。
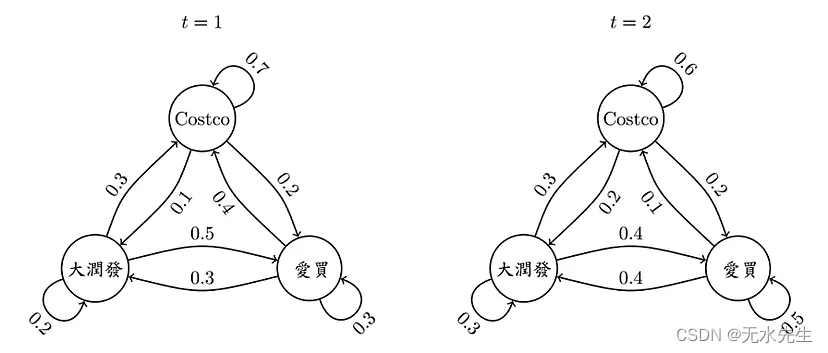
(2)学员圆仔每日到某卖场的机率,会受到前一日或是前两日去过哪间卖场的影响,前者称为 first-order,后者称为 second-order,听起来很难,其实也没什么,图画出来就知道简单了。
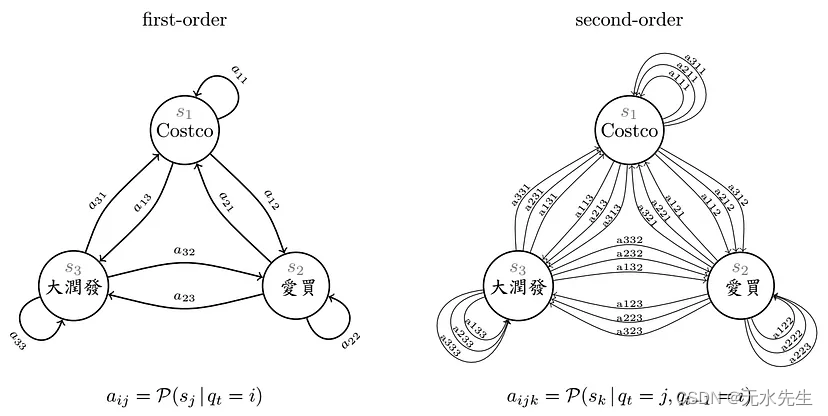
这些东西到底哪时候才会用到呢? 只要有时间关系的,例如,RNN、NLP、RL,都可以用 Markov chain 的变化形态来解释喔!
下一章 Hidden Markov Model_part2 会带大家认识闻风丧胆的「Hidden Markov Model」,敬请期待吧!!
六、介绍隐藏式马可夫法则。
Key point:
我们用 part 1 的例子做延伸,如下图,每天都有一定的机率到某间卖场里购物,同时也会有某个机率在该间卖场买瓶饮料。
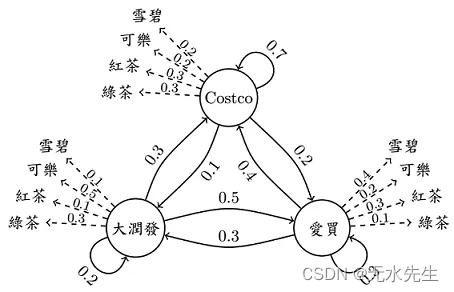
在起始机率分别为0.5、0.1、0.4下,圆仔三天来逛卖场的顺序为Q(爱买,Costco, 大润发),每到一间卖场他都会买一瓶饮料,三天来分别买了O(雪碧,可乐,绿茶),请问发生Q和O的共同机率为多少呢?

现在换个问题来想想,如果已知连续三天到卖场买的饮料依序为O(红茶,雪碧,绿茶),请问有几种可能路线呢? 每条路线分别发生的机率又有多少呢?
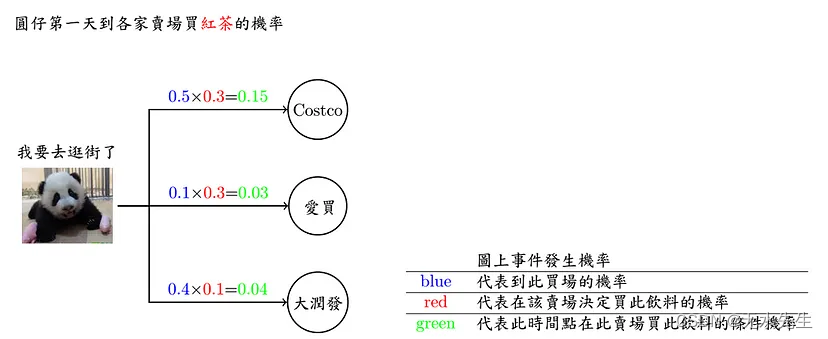
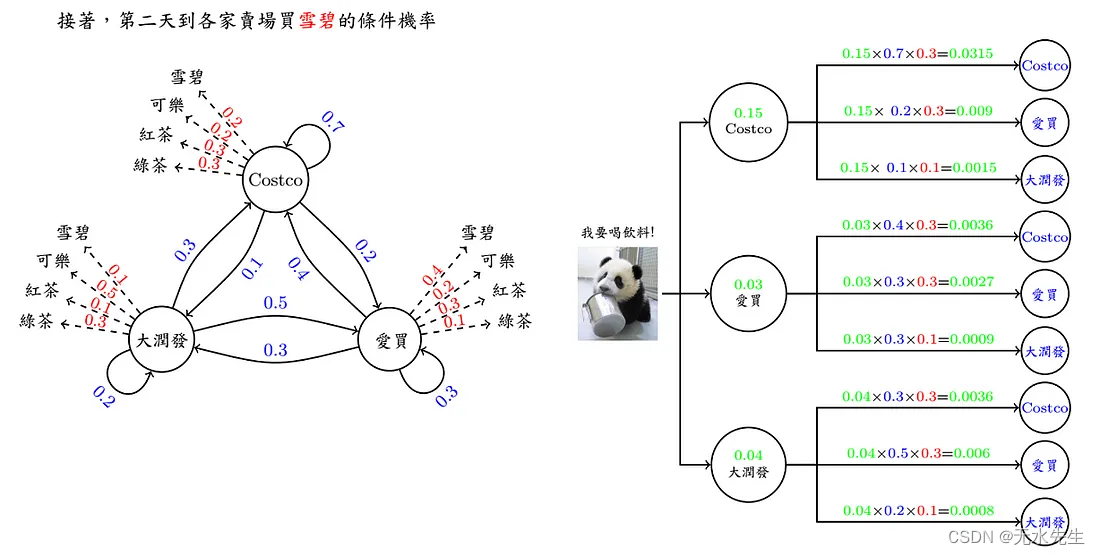
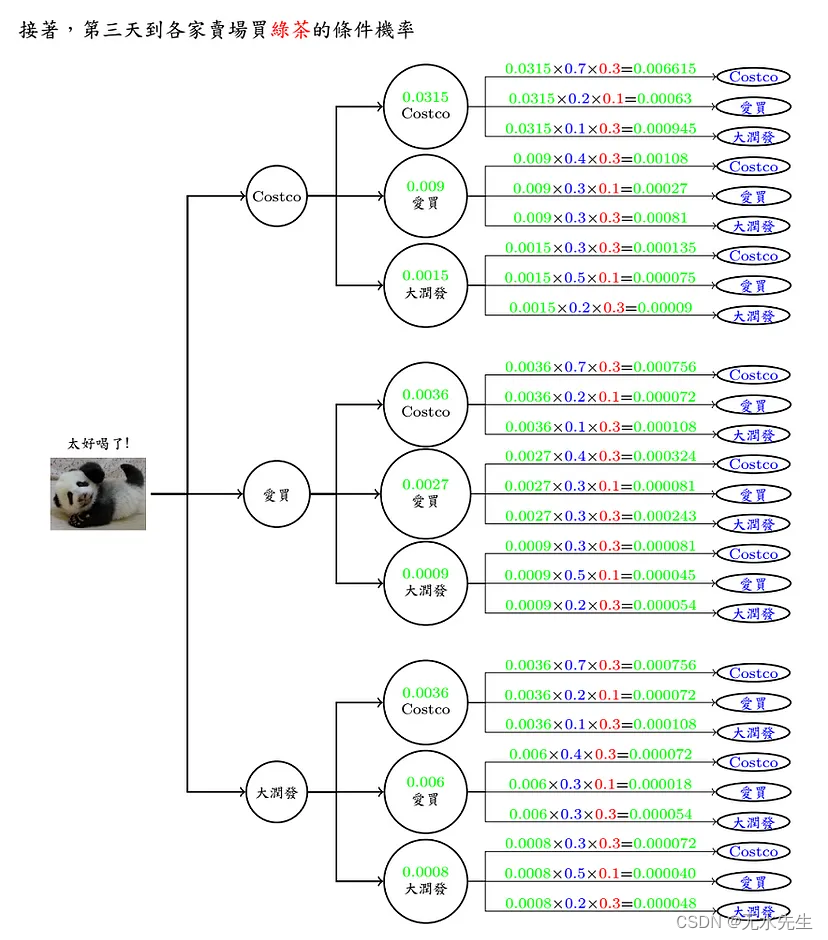

七、隐藏马尔可夫Introduction
第二个例子说明了,当只知观察值,而状态被隐藏的时候,如何找出「最佳的路径」。 但是,既然是 model 一定是需要训练的,到底什么东西是需要被训练的呢?
在实际遇到的问题中,我们并不会知道「机率转移矩阵」实际的机率是多少,换句话说,我们不知道上述所指的 「转移矩阵 A」和「转移矩阵 B」,只会有一堆数据。
在此,我们用已知的转移矩阵条件下,举一个实际的分类问题,熊猫团团、圆圆、圆仔,半年来,每周买饮料(观察值)的依序清单,至于可能的路线,及多少机率会买到对应的饮料,皆是未知,根据个别的买卖习惯分析,训练对应的模型,找出对应的「转移矩阵」,最后我们要预测,当随便给一周的饮料的清单,最有可能是哪只熊猫的喜好。

(上图为 HMM,其中一种方法,目的试算出在指定事件的发生状态下,算出此事件发生的最大机率之路径 )
八、结论
HMM模型特点:
- HMM 是针对有关时间序列的数据所建立的模型。
- 是所有时间模型的鼻祖 (ex: RNN、NLP、RL 等)
讲到这边,大家对于 HMM 能处理的问题,应该有所认识了,part 3 将会带大家了解要如何训练 model ,找出可能的状态栏,不过这部分有很多的数学式在里面,千万别看到就头晕了,所以慎入呀
这篇关于深入浅出談 隐马尔可夫的概念(1/ 2)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







