本文主要是介绍拓扑排序、关键路径(AOV、AOE网),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
拓扑排序(AOV网)
相关知识
在现代化管理中,人们常用有向图来描述和分析一项工程的计划和实施过程,一个工程常被分为多个小的子工程,这些子工程被称为活动(Activity)。 在有向图中若以顶点表示活动,有向边表示活动之间的先后关系,这样的图简称为AOV网。 图中的拓扑排序算法(Topological Sort)可以给出一个活动的合法序列。
拓扑序列 设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列v1, v2, …, vn称为一个拓扑序列,当且仅当满足下列条件:若从顶点vi到vj有一条路径,则在顶点序列中顶点vi必在顶点vj之前。
拓扑排序 对一个有向图构造拓扑序列的过程称为拓扑排序 。
图的存储结构
采用邻接表存储 ,在顶点表中增加一个入度域 in。
栈S:存储所有无前驱的顶点。
拓扑排序算法——伪代码
- 栈S初始化;累加器count初始化;
- 扫描顶点表,将没有前驱的顶点压栈;
- 当栈S非空时循环 3.1 vj=退出栈顶元素;输出vj;累加器加1; 3.2 将顶点vj的各个邻接点的入度减1; 3.3 将新的入度为0的顶点入栈;
- if (count<vertexNum) 输出有回路信息;
输入输出
第一行输入顶点个数和边的个数 后续行输入边依附的两个顶点的数字编号(测试用例的编号都从0开始) 输出拓扑排序的结果。如果存在环,输出拓扑排序的部分结果,再输出“图中存在环,无法拓扑排序”。
测试数据1
输入
7 10
0 2
0 3
1 3
1 5
2 4
3 4
3 5
3 6
4 6
5 6
输出
1 0 2 3 4 5 6
测试数据2
输入
6 8
0 2
0 3
1 3
1 5
2 4
3 4
4 5
5 3
输出
1 0 2 图中存在环,无法拓扑排序
代码
#include<iostream>
#include<stack>
#include<cstring>
#define MAX 100
using namespace std;
typedef struct ArcNode //边结点
{int adjvex; //顶点下标ArcNode *next;
} ArcNode;
typedef struct
{int in; //in是入度int vertex; //顶点信息ArcNode *firstEdge;
} vertexNode,VertexNode[MAX];class ALGraph
{
private:int vertexNum,arcNum; //顶点数,边数VertexNode adjList; //顶点数组stack<vertexNode> s; //栈int count=0; //计数
public:ALGraph(int v[],int n,int e);void TopologicalSort(); //拓扑排序
};
void ALGraph::TopologicalSort()
{for(int i=0; i<vertexNum; i++) //in为0则压栈{if(adjList[i].in==0){s.push(adjList[i]);}}while(!s.empty()) //循环终止条件:栈为空{vertexNode v=s.top(); //弹栈输出s.pop();cout<<v.vertex<<" ";count++; //计数加一ArcNode *a=v.firstEdge;while(a) //对弹出的结点遍历,所有遍历过的结点的in-1{adjList[a->adjvex].in--;int tmp=adjList[a->adjvex].in;if(tmp==0) //如果某结点的in变为0,则将其压栈{s.push(adjList[a->adjvex]) ;}a=a->next;}}if(count<vertexNum)cout<<"图中存在环,无法拓扑排序";//如果计数小于顶点数则说明有环
}
ALGraph::ALGraph(int v[],int n,int e) //构造函数
{vertexNum=n;arcNum=e;for(int i=0; i<vertexNum; i++) //顶点初始化{adjList[i].in=0;adjList[i].vertex=v[i];adjList[i].firstEdge=NULL;}ArcNode *s;int vi,vj;for(int i=0; i<arcNum; i++){s=new ArcNode;cin>>vi>>vj;s->adjvex=vj;s->next=adjList[vi].firstEdge; //头插法adjList[vi].firstEdge=s;adjList[vj].in++; //入度加一}
}
int main()
{int n,e;cin>>n>>e;int v[MAX];for(int i=0; i<n; i++){v[i]=i;}ALGraph algraph(v,n,e);algraph.TopologicalSort();return 0;
}
关键路径(AOE网)
AOE网
在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,边上的权值表示活动的持续时间,称这样的有向图叫做边表示活动的网,简称AOE网。AOE网中没有入边的顶点称为始点(或源点),没有出边的顶点称为终点(或汇点)。
AOE网的性质
⑴ 只有在某顶点所代表的事件发生后,从该顶点出发的各活动才能开始; ⑵ 只有在进入某顶点的各活动都结束,该顶点所代表的事件才能发生。
关键路径
在AOE网中,从始点到终点具有最大路径长度(该路径上的各个活动所持续的时间之和)的路径称为关键路径。
关键活动
关键路径上的活动称为关键活动。
关键路径可能不只一条,重要的是找到关键活动
关键活动的计算方法
首先计算以下与关键活动有关的量:
⑴ 事件的最早发生时间ve[k]
⑵ 事件的最迟发生时间vl[k]
⑶ 活动的最早开始时间ee[i]
⑷ 活动的最晚开始时间el[i]
最后计算各个活动的时间余量 el[k] - ee[k],时间余量为0者即为关键活动。
关键路径算法
⑴ 事件的最早发生时间ve[k] ve[前驱结点]+边 最大的一组,顺着求
⑵ 事件的最迟发生时间vl[k] vl[后继结点]-边 最小的一组, 逆着求
⑶ 活动的最早开始时间ee[i] 边的起点的ve
⑷ 活动的最晚开始时间el[i] 边的终点的vl-边长
关键路径算法伪码
step1、求ve
调用拓扑排序函数,创建数组resultStack存储拓扑排序结果序列(存储下标)。 一边拓扑排序,一边计算ve。
遍历所有的出边,如果ve[前驱/起点]+边的权值>ve[后继/终点],更新ve的值
step2、求vl
把resultTop数组看成栈,汇点先出栈 初始化vl数组为即汇点的ve值,这个ve值是最大的
依次弹出resultTop数组的元素,按拓扑逆序求个顶点的vl值
当栈不为空时
resultStack出栈。inVex为起点,访问inVex为起点的所有终点。
取一个终点,计算起点的vl值。
如果vl[后继结点]-边<vl[前驱结点]
vl[inVex] = vl[后继结点]-边;
step3、从上往下扫描顶点表,处理每个顶点的边表,计算ee和el的值
活动最早开始时间ee,与当前边起点的ve值相等
活动最晚开始时间el,为当前边终点的vl值-边的权值
如果ee==el,输出关键路径
题目要求
通过求关键路径,计算完成整个工程至少需要多少时间
输入输出
第一行输入有向图的顶点个数和边的个数
下面多行输入边的起点和终点的编号和边的权值
输出第一行为所有关键路径的边。如果不能求关键路径,则输出“存在环,无关键路径。”
测试数据1
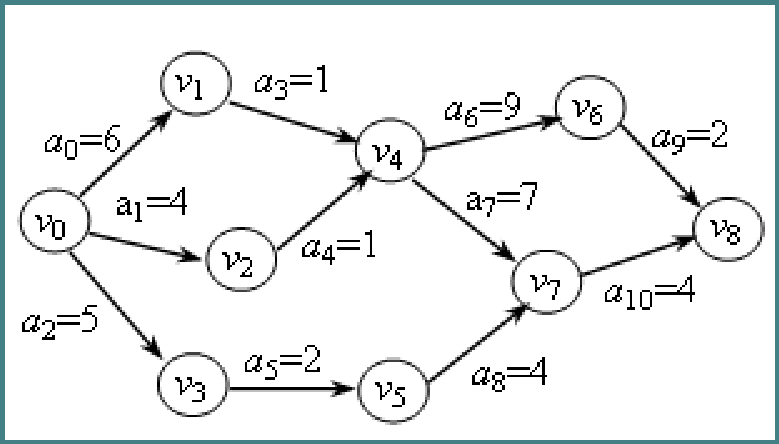
输入 9 11
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4
输出
<0,1>6 <1,4>1 <4,7>7 <4,6>9 <6,8>2 <7,8>4
测试数据2
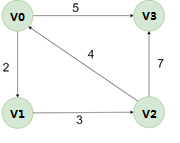
输入: 4 5
0 1 2
1 2 3
2 0 4
0 3 5
2 3 7
输出:
存在环,无关键路径。
代码
#include <iostream>
#include <stdio.h>
using namespace std;
const int MAX = 30;
struct ArcNode
{int weight;int adjvex;ArcNode* next;
};
struct VertexNode
{int in; //入度char vertex; //图的顶点ArcNode* firstEdge; //指向第一个边表
};
class ALGraph
{
private:VertexNode* adjList; //邻接表int vertexNum, arcNum;int* ve, * vl; //分别为事件最早发生时间的数组,事件最迟发生时间的数组
public:ALGraph(char v[], int n, int e);~ALGraph();void inputEdges();bool setEdge(int vi, int vj, int weight); //设置边void display();bool Topological(int result[], int& count); //拓扑排序bool GriticalPath(); //求关键路径
};
ALGraph::ALGraph(char v[], int n, int e)
{vertexNum = n;arcNum = e;adjList = new VertexNode[vertexNum]; //创建for (int i = 0; i < vertexNum; i++){adjList[i].in = 0;adjList[i].vertex = v[i];adjList[i].firstEdge = NULL;}ve = new int[vertexNum];vl = new int[vertexNum];
}void ALGraph::inputEdges()
{//cout << "输入" << endl;for (int i = 0; i < arcNum; i++){int vi, vj, weight;cin >> vi >> vj >> weight;if (!setEdge(vi, vj, weight)){cout << "超过范围,重新输入" << endl;i--;}}
}
bool ALGraph::setEdge(int vi, int vj, int weight)
{ArcNode* s;if (vi >= 0 && vi < vertexNum && vj >= 0 && vj < vertexNum && vi != vj){//创建一个边结点vjs = new ArcNode;s->adjvex = vj;s->weight = weight;// 把边结点vj插入顶点表的vi项的邻接表中,成为第一个节点s->next = adjList[vi].firstEdge;adjList[vi].firstEdge = s;// 入度+1adjList[vj].in++;return true;}else{return false;}
}
ALGraph::~ALGraph()
{ArcNode* p, * pre;// 顶点表指向所有边的结点删除for (int i = 0; i < vertexNum; i++){p = adjList[i].firstEdge;adjList[i].firstEdge = NULL;while (p){pre = p;p = p->next;delete pre;}}delete[] adjList;delete[] ve;delete[] vl;
}
bool ALGraph::Topological(int result[], int& count)
{int stack[MAX];int top = -1;int inVex;int outVex;ArcNode* p;for (int i = 0; i < vertexNum; i++){ve[i] = 0;}for (int i = 0; i < vertexNum; i++){if (adjList[i].in == 0){stack[++top] = i;}}count = 0; //统计有多少个顶点被处理过了while (top != -1){inVex = stack[top--]; //出栈result[count] = inVex; //存入数组count++; //下一次存储//找出当前处理的顶点的所有边p = adjList[inVex].firstEdge;while (p) //扫描边表 “删掉”边{outVex = p->adjvex; //获取当前边表的终点值adjList[outVex].in--; //入度减1if (adjList[outVex].in == 0) //把入度为0的压入堆栈stack[++top] = outVex;if (ve[inVex] + p->weight > ve[outVex]) //找到最大的时间ve[outVex] = ve[inVex] + p->weight;p = p->next;}}// 判断排序是否正确if (count == vertexNum) //该拓扑排序是无环图{return true;}elsereturn false;}
bool ALGraph::GriticalPath()
{int resultStack[MAX]; //存储拓扑排序的序列的栈int resultTop; //栈顶指针ArcNode* p;int i, count;int inVex, outVex;if (!Topological(resultStack, count)){return false;}resultTop = count - 1; //指向栈顶inVex = resultStack[resultTop--]; //栈顶元素出栈//求Vl数组,倒序求最小值//初始化for (i = 0; i < vertexNum; i++){vl[i] = ve[inVex];}while (resultTop != -1){inVex = resultStack[resultTop--];p = adjList[inVex].firstEdge;while (p){outVex = p->adjvex;if (vl[inVex] > vl[outVex] - p->weight){vl[inVex] = vl[outVex] - p->weight;}p = p->next;}}for (inVex = 0; inVex < vertexNum; inVex++)//从上往下扫描边表{p = adjList[inVex].firstEdge;while (p){outVex = p->adjvex;int weight = p->weight;int ee = ve[inVex]; //活动的最早开始时间int el = vl[outVex] - weight; //活动的最晚开始时间if (ee == el){cout << "<" << inVex << "," << outVex << ">" << weight << " ";}p = p->next;}}return true;
}
int main()
{char vertex[MAX];int num, edge;cin >> num >> edge;for (int i = 0; i < num; i++){vertex[i] = i + '0';}ALGraph graph(vertex, num, edge);graph.inputEdges();//graph.display();if (!graph.GriticalPath()){cout << "存在环,无关键路径。";}// 自动调用析构函数释放程序return 0;
}这篇关于拓扑排序、关键路径(AOV、AOE网)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!