本文主要是介绍2779. 数组的最大美丽值,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
简单翻译一下题目意思:
- 对于每个
nums[i]都可以被替换成[nums[i]-k, nums[i]+k]区间中的任何数,区间左右是闭的。 - 在每个数字可以替换的前提下,返回数组中最多的重复数字的数量。
第一想法是用一个哈希表,Key 是可以被替换的数,Value 是这个数出现的次数,那最后遍历这个哈希表,找到 Value 最大的就可以。
class Solution {public int maximumBeauty(int[] nums, int k) {int n = nums.length;// 使用哈希表记录每个可能的值出现的次数Map<Integer, Integer> hashMap = new HashMap<>();for (int i = 0; i < n; i++) {// 计算当前元素左右 k 范围内的值int left = nums[i] - k;int right = nums[i] + k;// 在范围内的每个值都增加计数for (int j = left; j <= right; j++) {hashMap.merge(j, 1, Integer::sum);}}int res = 0;// 遍历哈希表,找到出现次数最多的值for (Map.Entry<Integer, Integer> entry : hashMap.entrySet()) {res = Math.max(res, entry.getValue());}return res;}
}
思路是没有问题的,问题是时间复杂度太高,超时。

这时候可以引入扫描线算法,样例 nums = [4,6,1,2], k = 2 对应的替换范围为:
- [2, 6]
- [-1, 3]
- [4, 8]
- [0, 4]
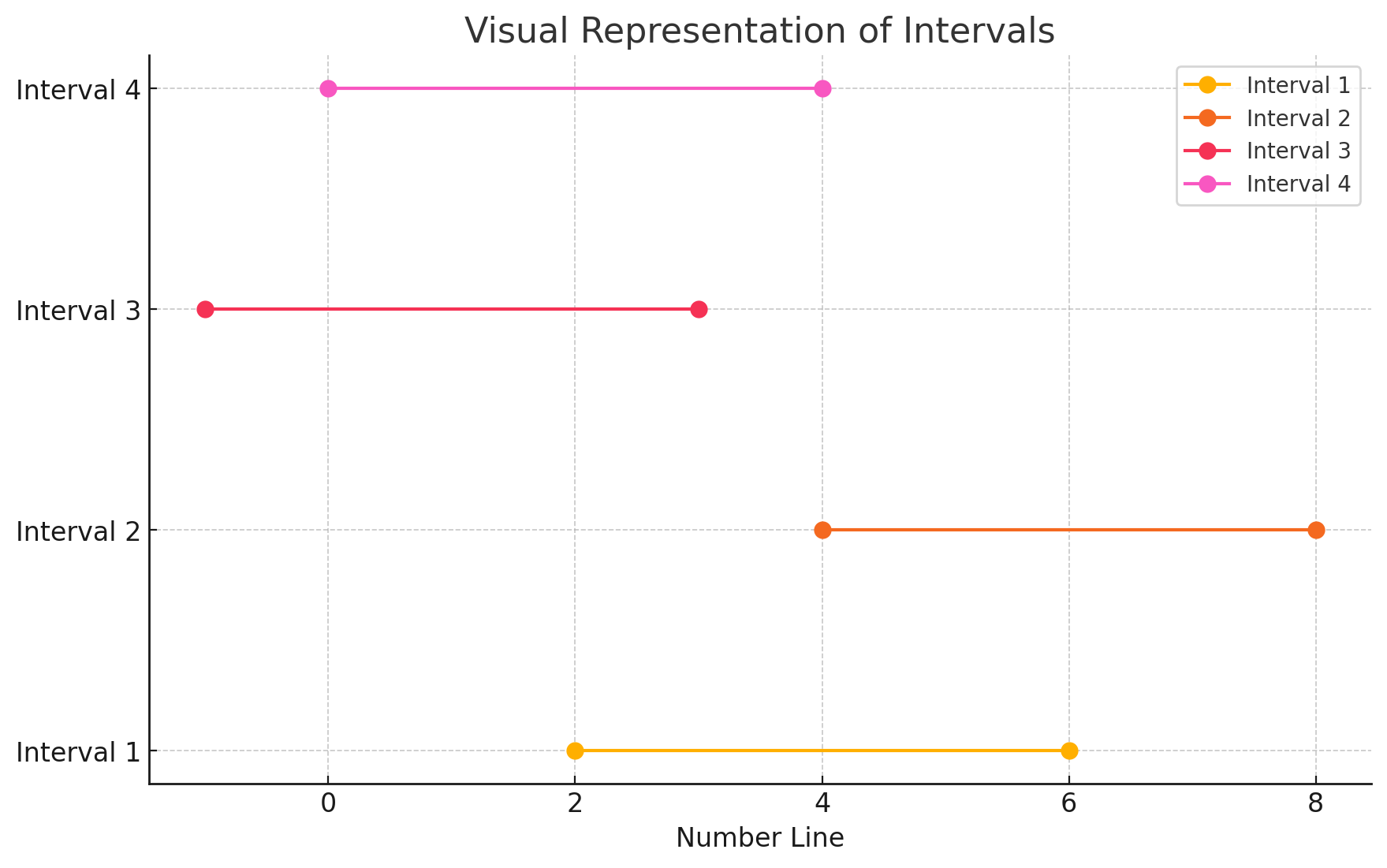
我们引入一根扫描线,从最小的区间起点开始扫描,计算这根线穿过的最多的区间数量,这个数即我们需要的最多重复数的数量,即「最大美丽值」。
class Solution {public int maximumBeauty(int[] nums, int k) {int n = nums.length;List<List<Integer>> intervals = new ArrayList<>();Arrays.sort(nums);// 为每个数字生成左右区间端点,并存入 intervals 列表for (int i = 0; i < n; i++) {int left = nums[i] - k;int right = nums[i] + k;// 左端点,+1 表示区间开始intervals.add(Arrays.asList(left, 1)); // 右端点,-1 表示区间结束intervals.add(Arrays.asList(right, -1)); }// 排序 intervals,按照左端点升序,左端点相同则按照右端点 +1 在前,-1 在后intervals.sort((a, b) -> {if (a.get(0).equals(b.get(0))) {return b.get(1) - a.get(1);}return a.get(0) - b.get(0);});// 记录最大重叠数int res = 0;// 扫描线变量,记录当前重叠区间数int scan = 0; for (List<Integer> interval : intervals) {// 更新当前重叠区间数scan += interval.get(1); // 更新最大重叠数res = Math.max(res, scan); }// 返回最大重叠数return res; }
}
几个细节:
List<Integer>自定义排序时,记得用equals不要用==。- 先按时间排,时间一样再按开始和结束区间排,开始区间在结束区间前处理。
- 扫描线遇到开始区间,就增加一个重复数,遇到一个结束区间,就减少一个重复数。
这篇关于2779. 数组的最大美丽值的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


