本文主要是介绍微服务SpringCloud ES分布式全文搜索引擎简介 下载安装及简单操作入门,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Elasticsearch
ES简介

分布式全文搜索引擎
我们天天在用ES
搜索的时候
要与多个信息进行匹配查找
然后返回给用户

首先
ES会将数据库中的信息
先进行一个拆分
这个叫做分词
是按照词语关键词拆的
然后就能进行搜索的时候匹配对应的id
每一个关键字对应若干id
每一个id对应数据
然后搜索的时候展示简化版数据
点击简化版数据反映全部信息属于的是全文搜索

在数据库中有索引
在ES中也有索引
但是根据关键字查ID 再由ID查数据
这个在全文搜索里叫倒排索引
倒排索引是怎么出现的呢
是根据创建文档 出现一个一个的库
然后我们进行查找的时候就是在使用这个库,使用文档

ES的下载和安装
下载地址
Download Elasticsearch | Elastic
下载好了

内置
有个jdk17
250MB左右
总大小600MB
双击初始化
文件: elasticsearch.bat

查找端口

访问本地地址
http://localhost:9200/
http://localhost:9200/即可访问到
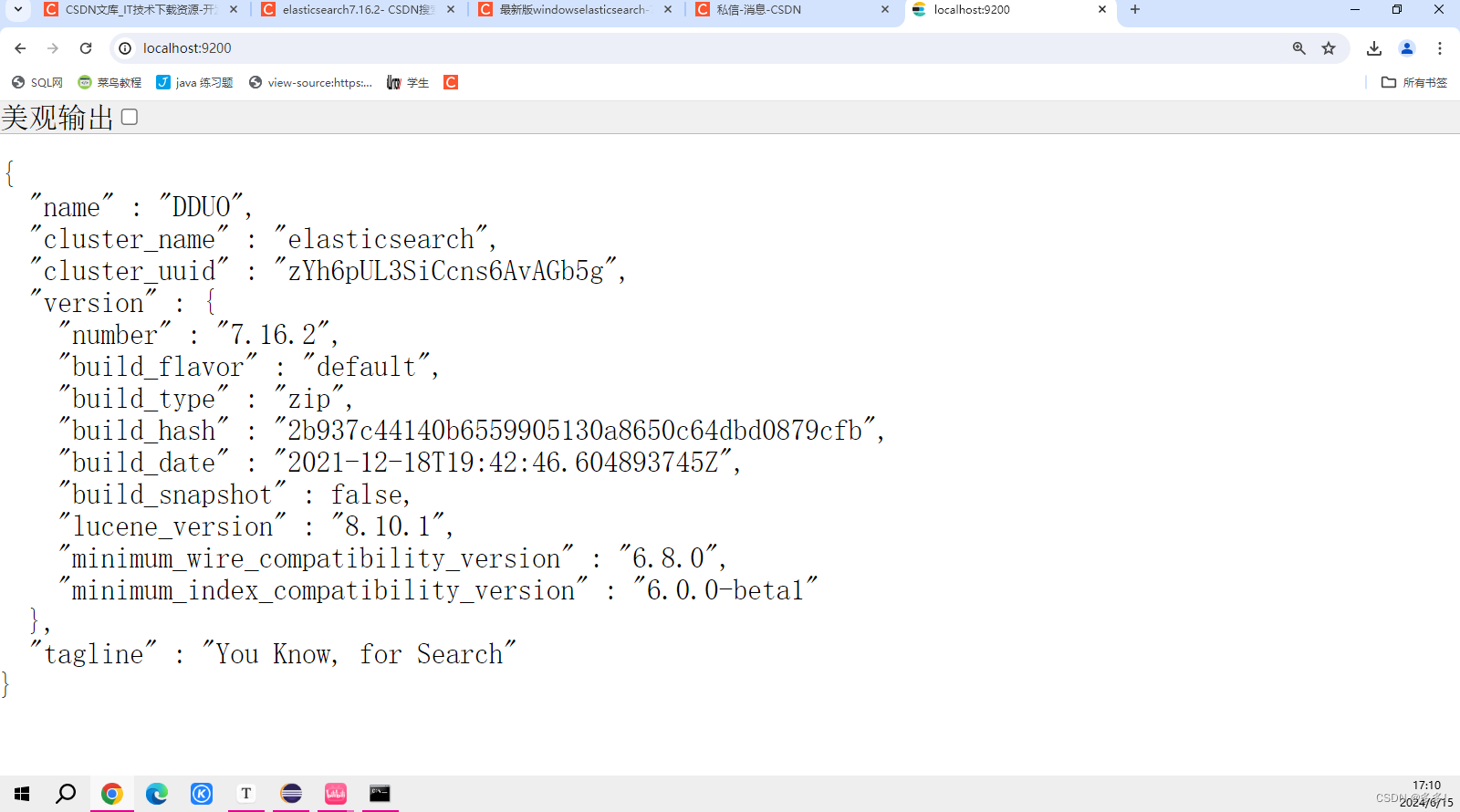
成功监测访问成功 部署成功
ES索引操作
ES没有数据库的概念
只有索引
我们可以把ES里的索引理解成数据库
用postman进行测试操作

创建一个名字叫books的索引
数据库

表示本次操作成功

索引不允许重复创建
如果再次创建就会报错
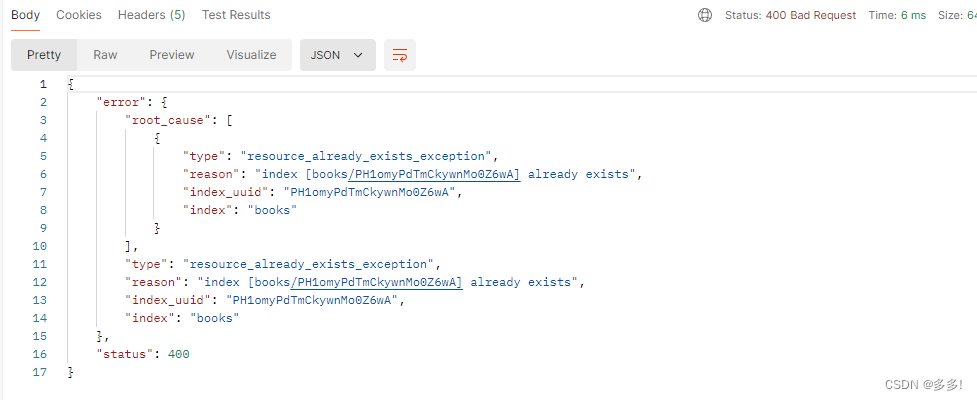
我们可以进行查询
用get进行查询

返回结果
代表查询成功
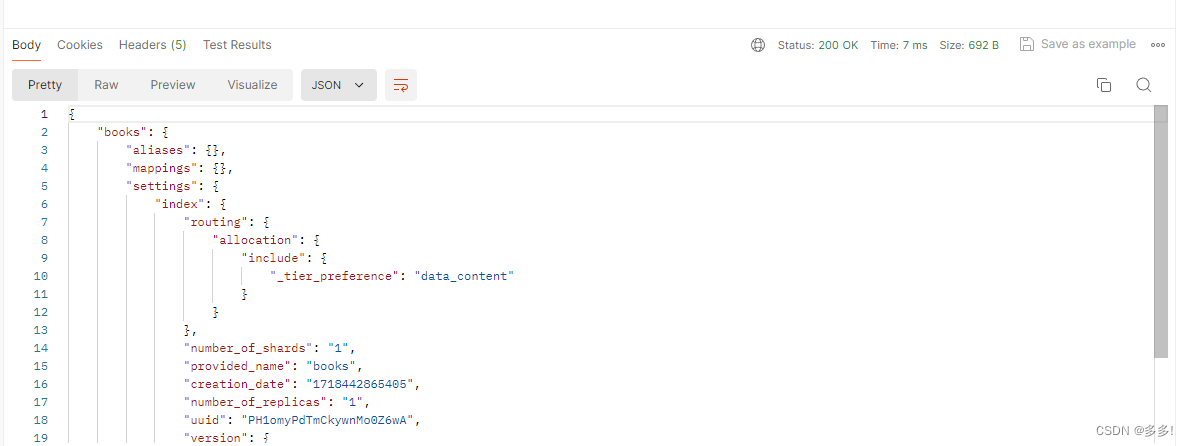
同样的我们通过不同的请求操作
能完成对索引的不同操作
需要的是路径和请求一一对应
幂等性是指一个操作或函数被多次应用后所产生的效果与一次应用时的效果相同的性质。换句话说,如果对同一个对象或系统进行一次或多次操作,最终的状态或结果都是一致的,那么这个操作就是幂等的。
在Web开发中,HTTP方法如GET、PUT、DELETE等应该是幂等的。例如,无论你调用一次还是多次相同的HTTP PUT请求,资源的状态应该是相同的。
这个地方就是放索引的分词信息的

我们下载一个分词器
 看看
看看
我们把他放到es的plugins目录下
相当于是装了一个插件

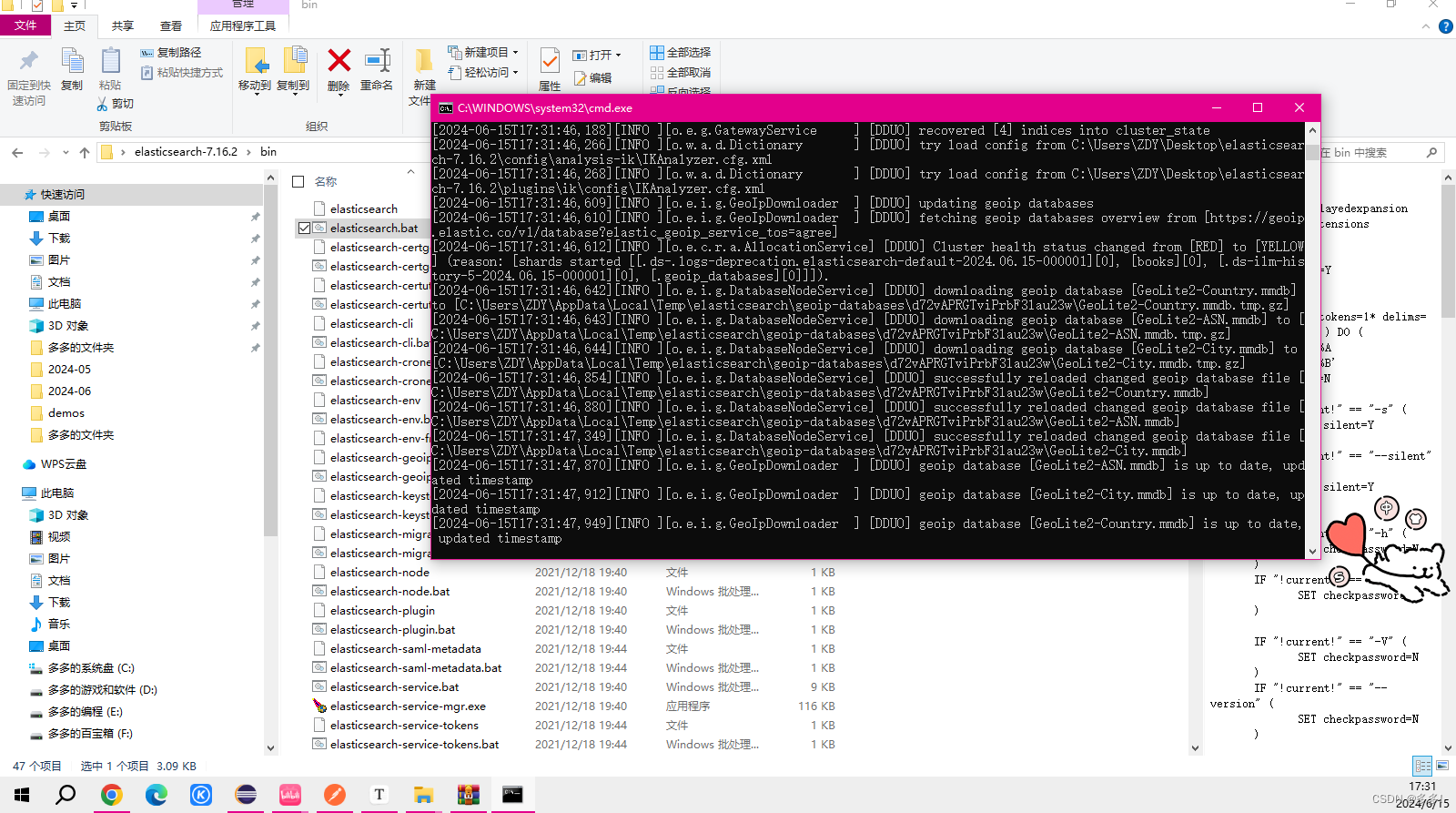
这时候我们要重新启动我们的ES
如果版本一致并且plugins文件夹下只有ik文件夹 即可启动成功
接下来我们就要去使用了
我们在postman里指定路径 在后面跟上一请求体的信息
在postman里写请求体

{"mappings":{"properties":{"id":{"type":"keyword","analyzer":"ik_max_word"},"name":{"type":"text","analyzer":"ik_max_word"},"type":{"type":"keyword"}}}
}发送后即创建成功

让索引挂上设定
然后数据进来的时候就会进行操作
小结


个人号推广
博客主页
多多!-CSDN博客
Web后端开发
https://blog.csdn.net/qq_30500575/category_12624592.html?spm=1001.2014.3001.5482
Web前端开发
https://blog.csdn.net/qq_30500575/category_12642989.html?spm=1001.2014.3001.5482
数据库开发
https://blog.csdn.net/qq_30500575/category_12651993.html?spm=1001.2014.3001.5482
项目实战
https://blog.csdn.net/qq_30500575/category_12699801.html?spm=1001.2014.3001.5482
算法与数据结构
https://blog.csdn.net/qq_30500575/category_12630954.html?spm=1001.2014.3001.5482
计算机基础
https://blog.csdn.net/qq_30500575/category_12701605.html?spm=1001.2014.3001.5482
回忆录
https://blog.csdn.net/qq_30500575/category_12620276.html?spm=1001.2014.3001.5482
这篇关于微服务SpringCloud ES分布式全文搜索引擎简介 下载安装及简单操作入门的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





