本文主要是介绍偏最小二乘模板,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
考虑到在分析酿酒葡萄理化指标与葡萄酒的理化指标之间联系时,理化指标的个数过多,并且各成分之间可能存在相互依赖的关系,比如各类氨基酸等,所以要想找出酿制前后成分的联系,可以采用偏最小二乘回归分析的方法,下面对该方法进行简要介绍。
偏最小二乘回归分析法集中了主成分分析、典型相关分析和线性回归分析方法的特点,主要研究两组多重相关变量间的相互依赖关系,并可以研究用一组变量去预测另一组变量,特别是当两组变量的个数很多,且都存在多重相关性而观测数据的数量较少时,用该方法建立的具有传统的经典回归分析等方法所没有的优点。
对于
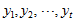
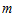
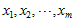
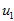
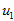
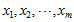
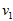
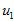
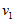
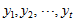
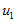
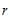
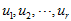
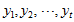
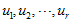
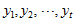
数据标准化。
将各指标值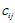
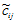
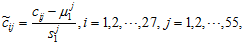
其中,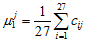
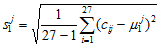

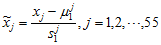
为标准化指标变量。
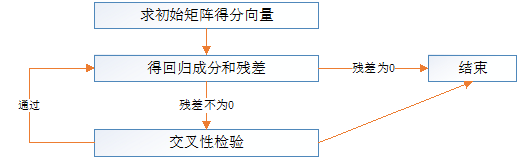
求解框图
案列分析:
191 36 50 5 162 60
189 37 52 2 110 60
193 38 58 12 101 101
162 35 62 12 105 37
189 35 46 13 155 58
182 36 56 4 101 42
211 38 56 8 101 38
167 34 60 6 125 40
176 31 74 15 200 40
154 33 56 17 251 250
169 34 50 17 120 38
166 33 52 13 210 115
154 34 64 14 215 105
247 46 50 1 50 50
193 36 46 6 70 31
202 37 62 12 210 120
clc,clear
load pz.txt %原始数据存放在纯文本文件pz.txt中
mu=mean(pz);sig=std(pz); %求均值和标准差
rr=corrcoef(pz); %求相关系数矩阵
data=zscore(pz); %数据标准化
%只要更改这里确定自变量和因变量即可
n=3;m=3; %n是自变量的个数,m是因变量的个数
x0=pz(:,1:n);y0=pz(:,n+1:end);
e0=data(:,1:n);f0=data(:,n+1:end);
num=size(e0,1);%求样本点的个数
chg=eye(n); %w到w*变换矩阵的初始化
for i=1:n
%以下计算w,w*和t的得分向量,
matrix=e0'*f0*f0'*e0;
[vec,val]=eig(matrix); %求特征值和特征向量
val=diag(val); %提出对角线元素
[val,ind]=sort(val,'descend');
w(:,i)=vec(:,ind(1)); %提出最大特征值对应的特征向量
w_star(:,i)=chg*w(:,i); %计算w*的取值
t(:,i)=e0*w(:,i); %计算成分ti的得分
alpha=e0'*t(:,i)/(t(:,i)'*t(:,i)); %计算alpha_i
chg=chg*(eye(n)-w(:,i)*alpha'); %计算w到w*的变换矩阵
e=e0-t(:,i)*alpha'; %计算残差矩阵
e0=e;
%以下计算ss(i)的值
beta=[t(:,1:i),ones(num,1)]\f0; %求回归方程的系数
beta(end,:)=[]; %删除回归分析的常数项
cancha=f0-t(:,1:i)*beta; %求残差矩阵
ss(i)=sum(sum(cancha.^2)); %求误差平方和
%以下计算press(i)
for j=1:num
t1=t(:,1:i);f1=f0;
she_t=t1(j,:);she_f=f1(j,:); %把舍去的第j个样本点保存起来
t1(j,:)=[];f1(j,:)=[]; %删除第j个观测值
beta1=[t1,ones(num-1,1)]\f1; %求回归分析的系数
beta1(end,:)=[]; %删除回归分析的常数项
cancha=she_f-she_t*beta1; %求残差向量
press_i(j)=sum(cancha.^2);
end
press(i)=sum(press_i);
if i>1
Q_h2(i)=1-press(i)/ss(i-1);
else
Q_h2(1)=1;
end
if Q_h2(i)<0.0975
fprintf('提出的成分个数r=%d',i);
r=i;
break
end
end
beta_z=[t(:,1:r),ones(num,1)]\f0; %求Y关于t的回归系数
beta_z(end,:)=[]; %删除常数项
xishu=w_star(:,1:r)*beta_z; %求Y关于X的回归系数,且是针对标准数据的回归系
%数,每一列是一个回归方程
mu_x=mu(1:n);mu_y=mu(n+1:end);
sig_x=sig(1:n);sig_y=sig(n+1:end);
for i=1:m
ch0(i)=mu_y(i)-mu_x./sig_x*sig_y(i)*xishu(:,i); %计算原始数据的回归方程的常数项
end
for i=1:m
xish(:,i)=xishu(:,i)./sig_x'*sig_y(i); %计算原始数据的回归方程的系数,每一列是一个回归方程
end
sol=[ch0;xish] %显示回归方程的系数,每一列是一个方程,每一列的第一个数是常数项
这篇关于偏最小二乘模板的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




