深入理解计算机系统 家庭作业6.34

本文主要是介绍深入理解计算机系统 家庭作业6.34，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

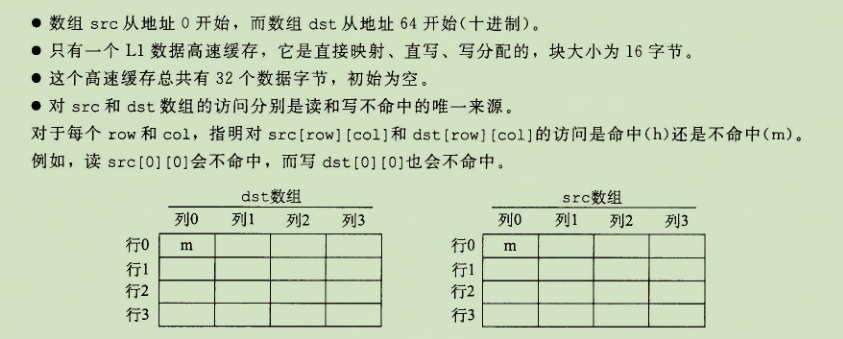
第一步先求(S,E,B,m)

题目说共C=32个字节,块大小B为16个字节,那就是分为两组:0,1.然后每组存4个int 每个4字节

C=B*E*S .B=16 ,直接映射的E就是1,所以S=2

m为啥等于7? 通过写出两个数组所有的地址可以得出m=7.

得出高速缓存的参数:(S,E,B,m)=(2,1,16,7),注意图6-26每个参数的定义即可算出:

C	32
M	128
s	1
b	4
t	2

此时脑海已经有了缓存的结构了

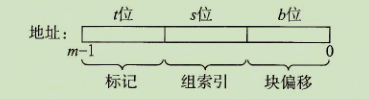
从图6-26的定义和我们算出来的参数就得出:

题目说数组src从0开始 因为sizeof(int)==0100 所以每个元素的地址+100就是下个元素的地址啦

加到dst[0][0]你发现刚好就等于二进制1000000 也就是十进制的64.这两个数组是紧挨着的

sizeof(int)==0100	虚拟地址(二进制)	CO	CI	CT
src[0][0]	0000000	0000	0	00
src[0][1]	0000100	0100	0	00
src[0][2]	0001000	1000	0	00
src[0][3]	0001100	1100	0	00
src[1][0]	0010000	0000	1	00
src[1][1]	0010100	0100	1	00
src[1][2]	0011000	1000	1	00
src[1][3]	0011100	1100	1	00
src[2][0]	0100000	0000	0	01
src[2][1]	0100100	0100	0	01
src[2][2]	0101000	1000	0	01
src[2][3]	0101100	1100	0	01
src[3][0]	0110000	0000	1	01
src[3][1]	0110100	0100	1	01
src[3][2]	0111000	1000	1	01
src[3][3]	0111100	1100	1	01
dst[0][0]	1000000	0000	0	10
dst[0][1]	1000100	0100	0	10
dst[0][2]	1001000	1000	0	10
dst[0][3]	1001100	1100	0	10
dst[1][0]	1010000	0000	1	10
dst[1][1]	1010100	0100	1	10
dst[1][2]	1011000	1000	1	10
dst[1][3]	1011100	1100	1	10
dst[2][0]	1100000	0000	0	11
dst[2][1]	1100100	0100	0	11
dst[2][2]	1101000	1000	0	11
dst[2][3]	1101100	1100	0	11
dst[3][0]	1110000	0000	1	11
dst[3][1]	1110100	0100	1	11
dst[3][2]	1111000	1000	1	11
dst[3][3]	1111100	1100	1	11

每次读16字节那就是读数组的一行,读到的数放在组0还是组1取决于上表中被读元素地址的CI位

i=0,j=0	=>	i=0,j=3
读src[0][0]					写dst[0][0]
组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]	组0:	dst[0][0]	dst[0][1]	dst[0][2]	dst[0][3]
组1:					组1:
读src[0][1]					写dst[1][0]
组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]	组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]
组1:					组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]
读src[0][2]	命中				写dst[2][0]
组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]	组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]
组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]	组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]
读src[0][3]					写dst[3][0]
组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]	组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]
组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]	组1:	dst[3][0]	dst[3][1]	dst[3][2]	dst[3][3]
i=1,j=0	=>	i=1,j=3
读src[1][0]					写dst[0][1]
组0:					组0:	dst[0][0]	dst[0][1]	dst[0][2]	dst[0][3]
组1:	src[1][0]	src[1][1]	src[1][2]	src[1][3]	组1:	src[1][0]	src[1][1]	src[1][2]	src[1][3]
读src[1][1]	命中				写dst[1][1]
组0:	dst[0][0]	dst[0][1]	dst[0][2]	dst[0][3]	组0:	dst[0][0]	dst[0][1]	dst[0][2]	dst[0][3]
组1:	src[1][0]	src[1][1]	src[1][2]	src[1][3]	组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]
读src[1][2]					写dst[2][1]
组0:	dst[0][0]	dst[0][1]	dst[0][2]	dst[0][3]	组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]
组1:	src[1][0]	src[1][1]	src[1][2]	src[1][3]	组1:	src[1][0]	src[1][1]	src[1][2]	src[1][3]
读src[1][3]	命中				写dst[3][1]
组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]	组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]
组1:	src[1][0]	src[1][1]	src[1][2]	src[1][3]	组1:	dst[3][0]	dst[3][1]	dst[3][2]	dst[3][3]
i=2,j=0	=>	i=2,j=3
读src[2][0]					写dst[0][2]
组0:	src[2][0]	src[2][1]	src[2][2]	src[2][3]	组0:	dst[0][0]	dst[0][1]	dst[0][2]	dst[0][3]
组1:	dst[3][0]	dst[3][1]	dst[3][2]	dst[3][3]	组1:	dst[3][0]	dst[3][1]	dst[3][2]	dst[3][3]
读src[2][1]					写dst[1][2]
组0:	src[2][0]	src[2][1]	src[2][2]	src[2][3]	组0:	src[2][0]	src[2][1]	src[2][2]	src[2][3]
组1:	dst[3][0]	dst[3][1]	dst[3][2]	dst[3][3]	组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]
读src[2][2]	命中				读dst[2][2]
组0:	src[2][0]	src[2][1]	src[2][2]	src[2][3]	组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]
组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]	组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]
读src[2][3]					读dst[3][2]
组0:	src[2][0]	src[2][1]	src[2][2]	src[2][3]	组0:	src[2][0]	src[2][1]	src[2][2]	src[2][3]
组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]	组1:	dst[3][0]	dst[3][1]	dst[3][2]	dst[3][3]
i=3,j=0	=>	i=3,j=3
读src[3][0]					读dst[0][3]
组0:	src[2][0]	src[2][1]	src[2][2]	src[2][3]	组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]
组1:	src[3][0]	src[3][1]	src[3][2]	src[3][3]	组1:	src[3][0]	src[3][1]	src[3][2]	src[3][3]
读src[3][1]	命中				读dst[1][3]
组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]	组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]
组1:	src[3][0]	src[3][1]	src[3][2]	src[3][3]	组1:	dst[1][0]	dst[1][1]	dst[1][2]	dst[1][3]
读src[3][2]					读dst[2][3]
组0:	src[0][0]	src[0][1]	src[0][2]	src[0][3]	组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]
组1:	src[3][0]	src[3][1]	src[3][2]	src[3][3]	组1:	src[3][0]	src[3][1]	src[3][2]	src[3][3]
读src[3][3]	命中				读dst[3][3]
组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]	组0:	dst[2][0]	dst[2][1]	dst[2][2]	dst[2][3]
组1:	src[3][0]	src[3][1]	src[3][2]	src[3][3]	组1:	dst[3][0]	dst[3][1]	dst[3][2]	dst[3][3]

这篇关于深入理解计算机系统 家庭作业6.34的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---