【C语言】递归复杂度与链表OJ之双指针

本文主要是介绍【C语言】递归复杂度与链表OJ之双指针，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【C语言】递归复杂度与链表OJ之双指针

🔥个人主页：大白的编程日记

🔥专栏：数据结构

---

前言

哈喽，各位小伙伴大家好！今天我们继续深入探讨递归的复杂度和链表OJ常见的双指针法。话不多说，咱们进入正题！向大厂冲锋！

一.递归复杂度

1.1递归时间复杂度

前面我们讲的复杂度没有涉及到递归，那递归的复杂度又该如何计算呢？

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}

之前我们都是在一个函数中算时间算复杂度，但是递归会自己调用自己，所以递归的时间复杂度计算就需要把每次函数调用次数累加起来。

那我们现在修改一下代码，现在的时间复杂度又是多少呢？

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{if (0 == N)return 1;for (int i = 0; i < N; i++){;}return Fac(N - 1) * N;
}

函数的调用次数不变，每次函数调用的复杂度改变。将每次函数调用的消耗相加
，时间复杂度函数为等差数列。大O渐进表示法算出O（N^2）。

结论：递归时间复杂度==所有递归递归调用次数累加。

现在我们再来计算一下斐波那契数列的时间复杂度。

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

这里我们需要画出递归展开图，然后发现调用次数是等比数列。
再用错位相减法计算调用次数即可。实际调用次数没那么多。
但是也是O(2^N)的量级。

1.2递归空间复杂度

那递归的复杂度又该如何计算呢？

• 阶乘
  递归会调用函数，每次调用函数都会开辟栈帧。
  所以递归的空间复杂度是函数调用的次数。

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}

• 斐波那契数列

// 计算斐波那契递归Fib的空间复杂度？
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

斐波那契数列的递归是双倍递归，那他的空间复杂度该如何计算呢？

因为函数栈帧会重复利用，所以斐波那契数列的空间复杂度就是O(N)。

二.链表OJ之双指针

2.1倒数第K个节点

• 题目
  倒数第k个节点
  

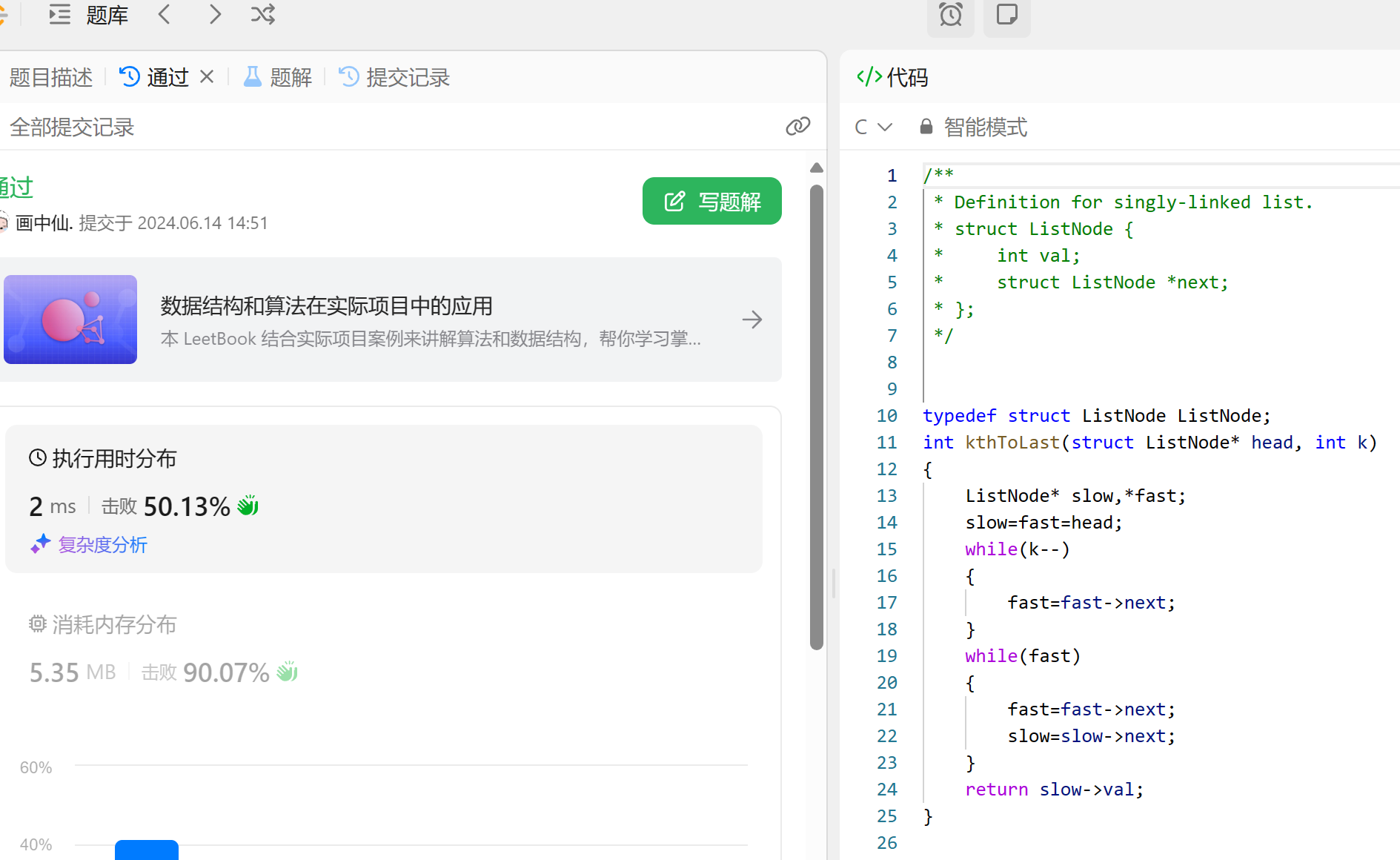
• 思路分析

我们先让快慢指针拉开k步，当快指针到NULL节点，慢指针就是倒数第K个节点。

• 代码

typedef struct ListNode ListNode;
int kthToLast(struct ListNode* head, int k)
{ListNode* slow,*fast;slow=fast=head;while(k--){fast=fast->next;}while(fast){fast=fast->next;slow=slow->next;}return slow->val;
}

2.2链表的中间节点

• 题目
  链表的中间节点
  
• 思路分析
  我们可以定义两个指针，一个每次走一步，一个每次走两步。
  

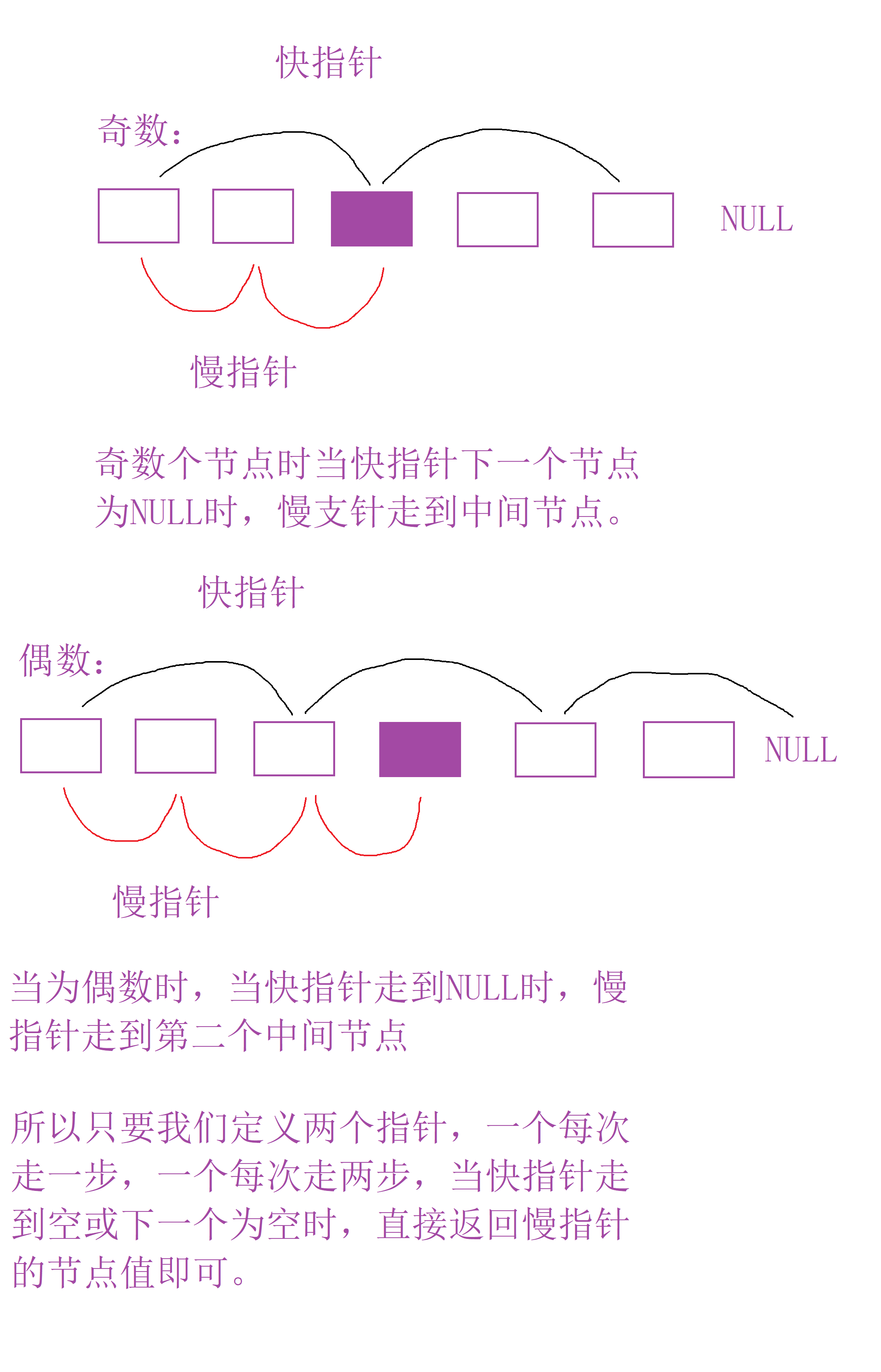
这就是我们的快慢指针。两个指针走的路程是2倍关系，当快指针走完时，慢指针也走了快指针的一半路程。

• 代码

 typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head){//创建快慢指针struct ListNode* slow;struct ListNode* fast;slow=fast=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;}//此时slow指向中间节点return slow;}

2.3反转链表

• 题目
  反转链表
  
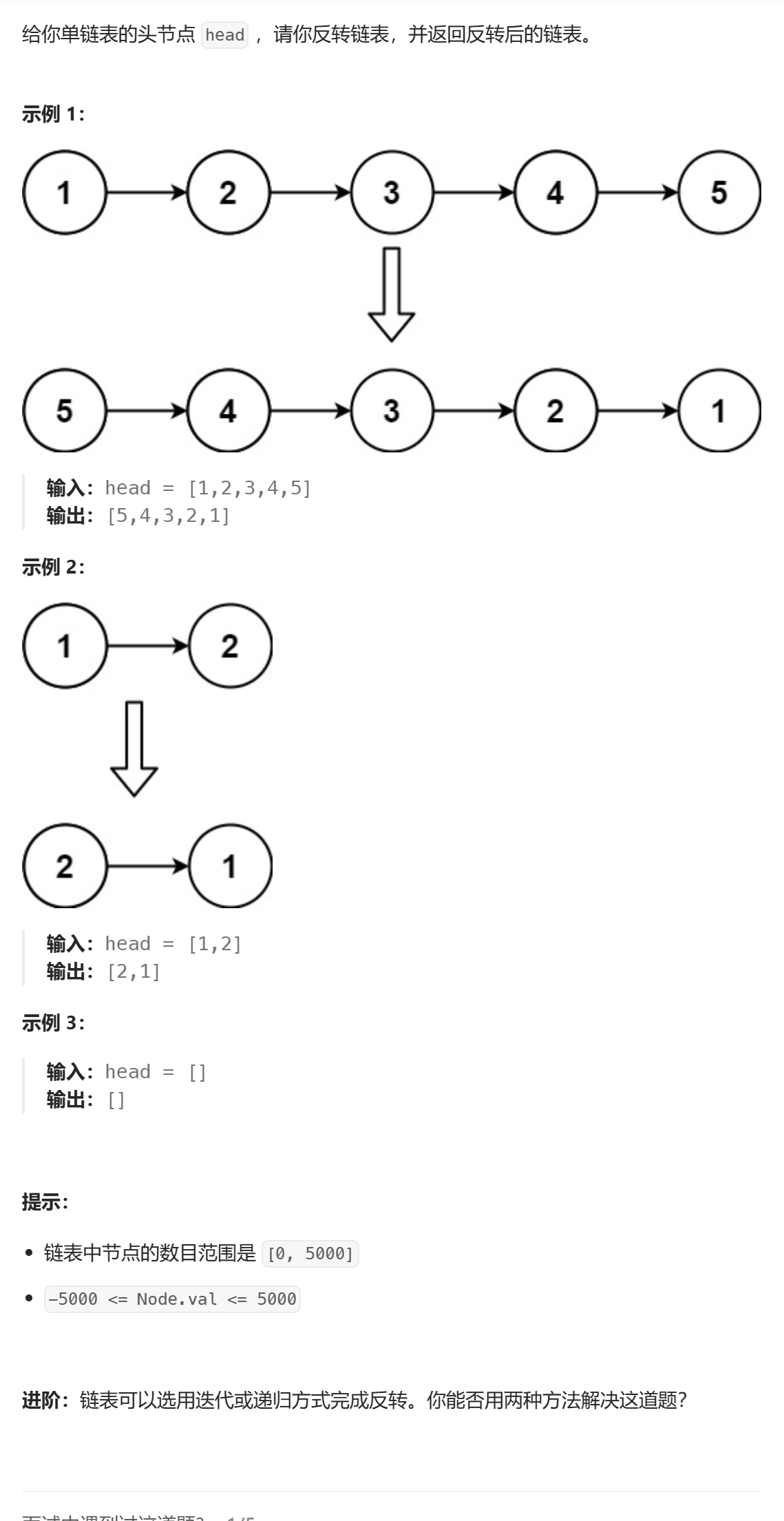
• 思路
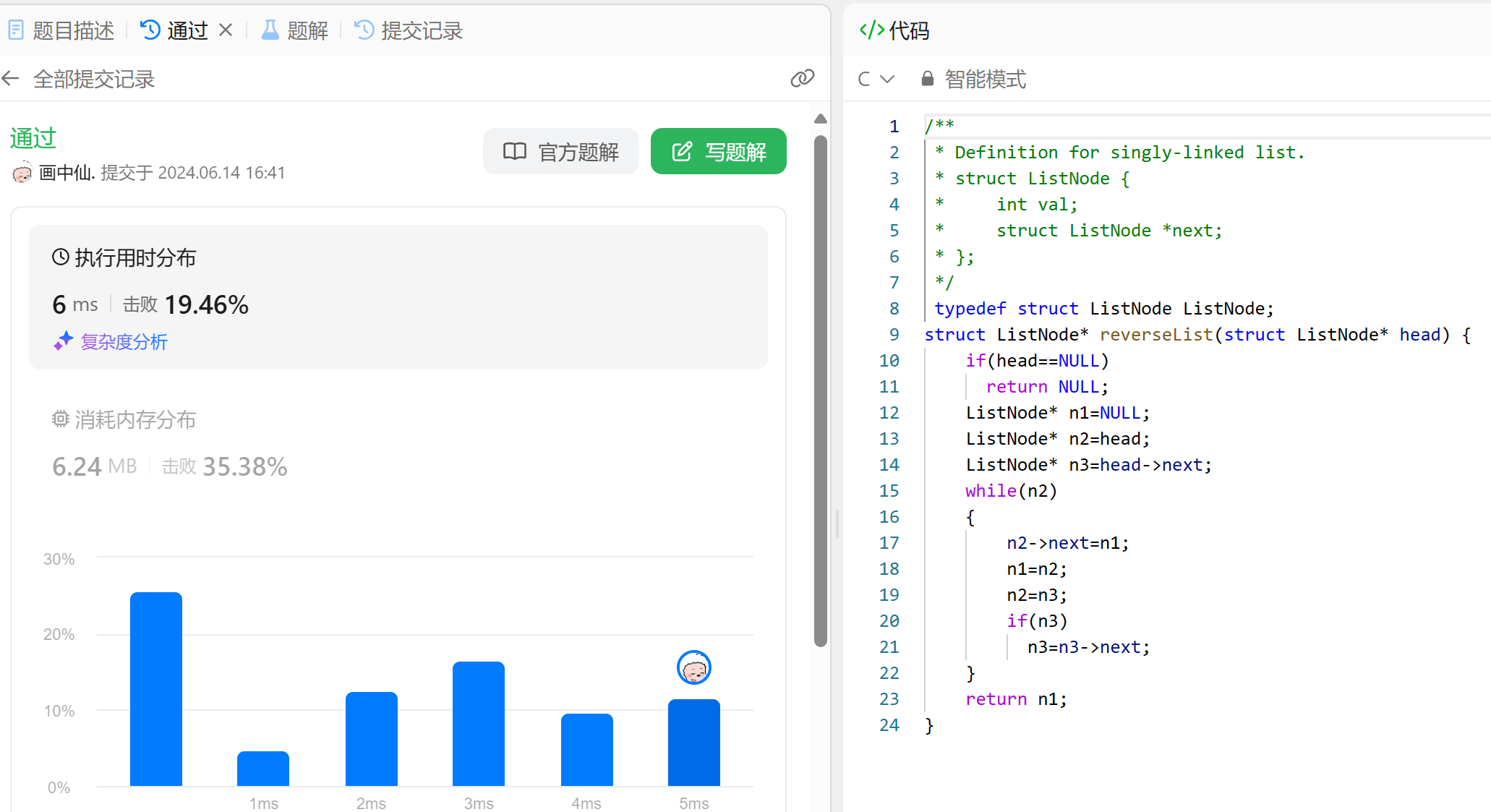
• 我们创建三个节点指针n1,n2,n3。n1刚开始指向NULL，n2指向头节点，n3保存n2的下一个几点。每次都让n2指向n1，然后n1移动到n2，n2移动到n3.n3向后移动。当n2走到尾节点就完成反转。
  
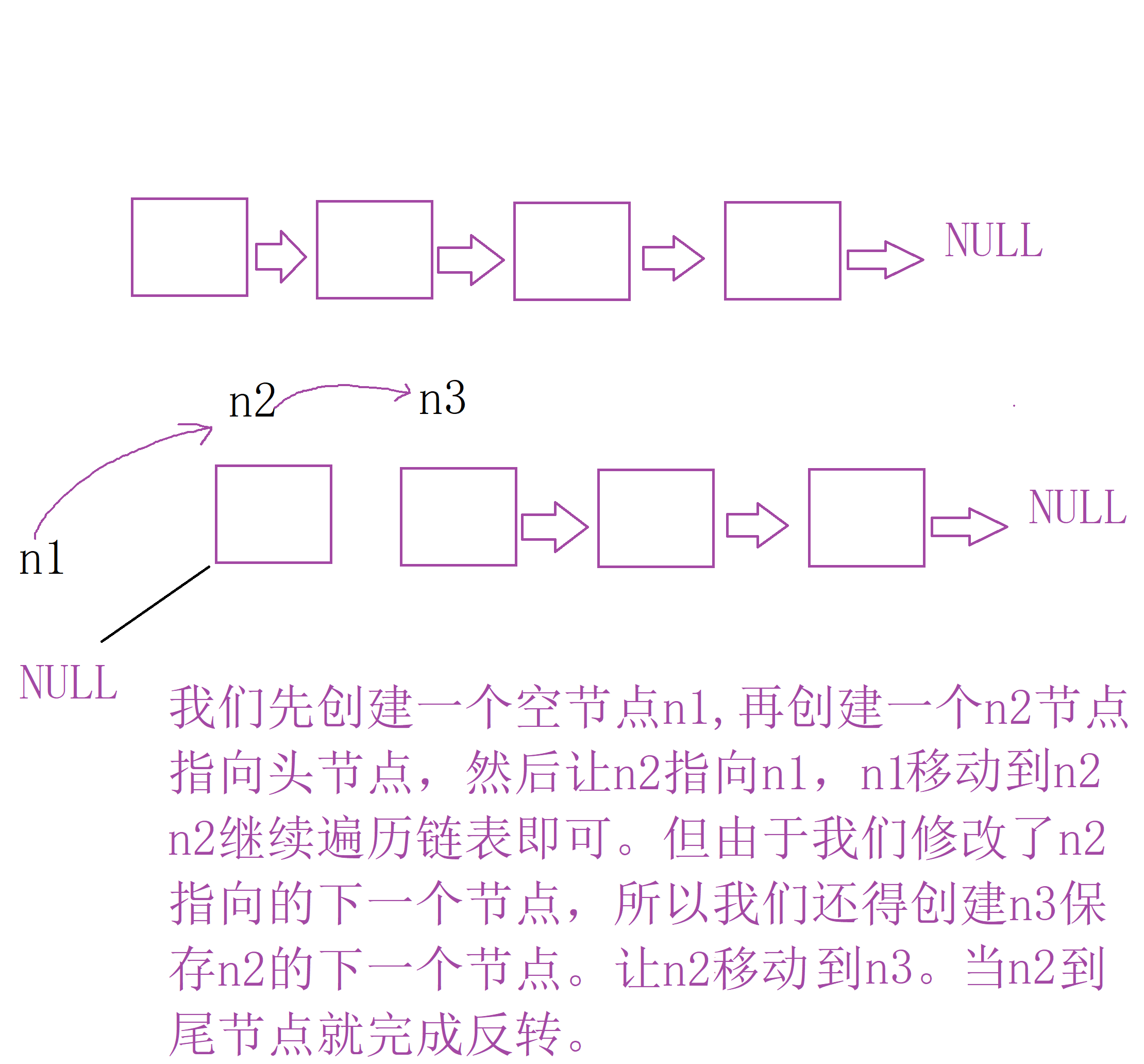
• 代码

 typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head) {if(head==NULL)return NULL;ListNode* n1=NULL;ListNode* n2=head;ListNode* n3=head->next;while(n2){n2->next=n1;n1=n2;n2=n3;if(n3)n3=n3->next;}return n1;
}

2.4回文链表

• 题目
  回文链表
  

• 思路

• 我们先找到中间节点，反转以中间节点为头节点的子链表。然后分别从头节点和中间节点开始遍历，一一对比，当中间节点走到NULL时，说明是回文链表。
  

• 代码

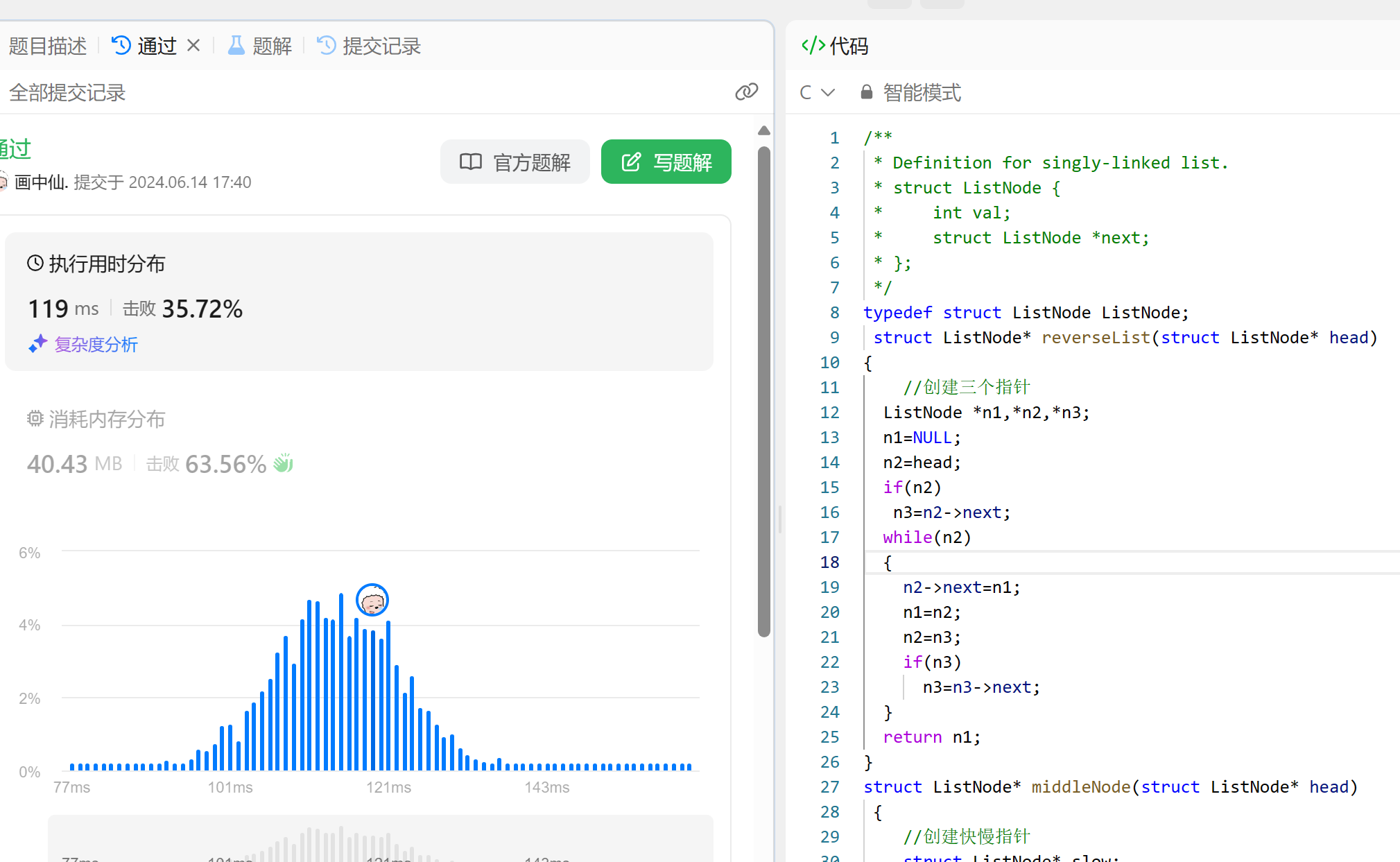
typedef struct ListNode ListNode;struct ListNode* reverseList(struct ListNode* head)
{//创建三个指针ListNode *n1,*n2,*n3;n1=NULL;n2=head;if(n2)n3=n2->next;while(n2){n2->next=n1;n1=n2;n2=n3;if(n3)n3=n3->next;}return n1;
}
struct ListNode* middleNode(struct ListNode* head){//创建快慢指针struct ListNode* slow;struct ListNode* fast;slow=fast=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;}//此时slow指向中间节点return slow;}
bool isPalindrome(struct ListNode* head) 
{ListNode* mid=middleNode(head);//找到中间节点ListNode* reverse=reverseList(mid);//反转后面节点ListNode*pcur=head;while(reverse){if(pcur->val!=reverse->val)//匹配{return false;break;}reverse=reverse->next;//移动pcur=pcur->next;}return true;
}

2.5相交链表

• 题目
  相交链表
  

• 思路

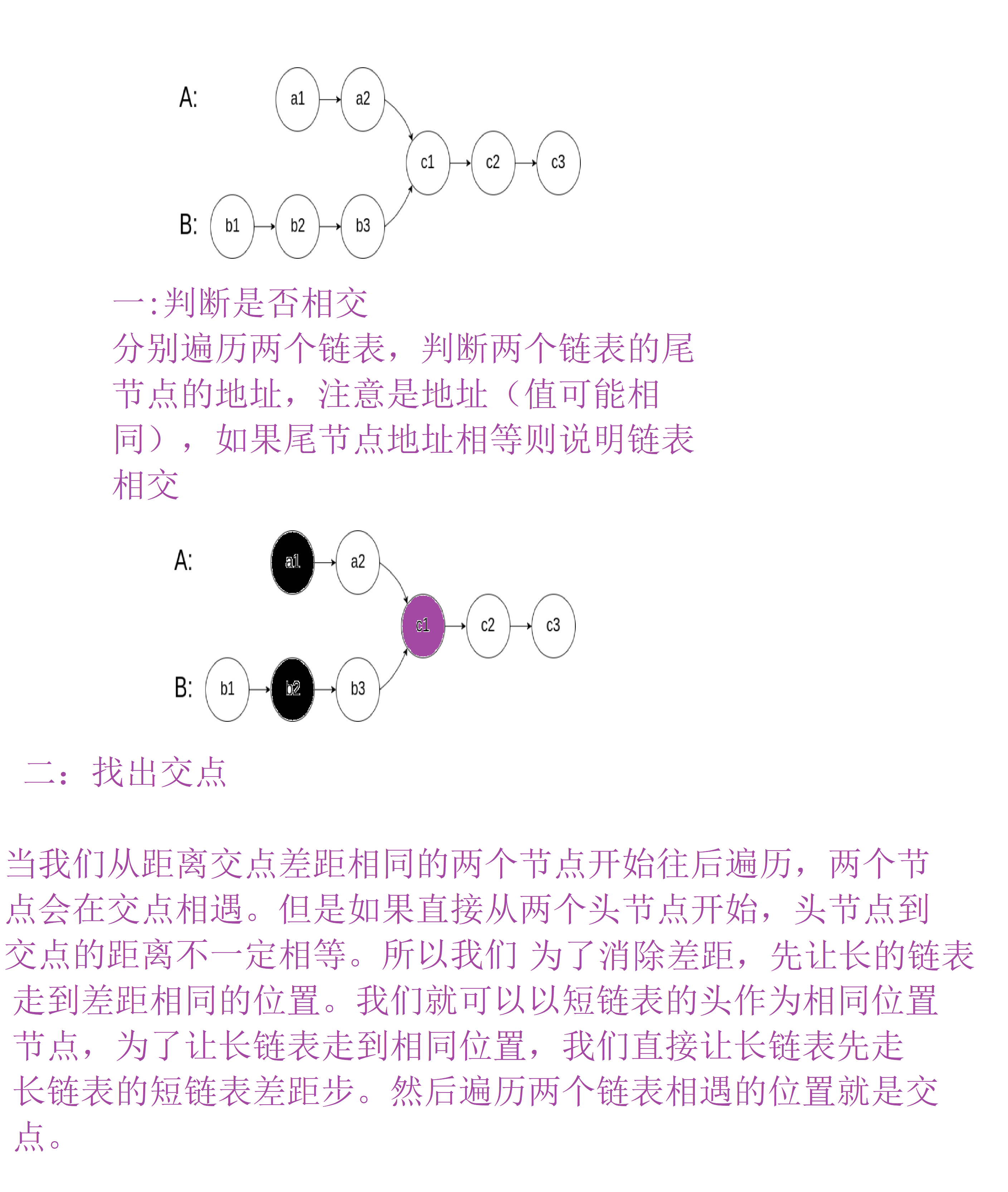
• 判断相交
  分别遍历两个链表到尾节点，判断尾节点地址是否相等。相等就相交

• 找交点
  让长链表走两链表长度的差距步，此时两节点距离交点差距相等。两节点同时往后遍历，相遇的位置就是交点。

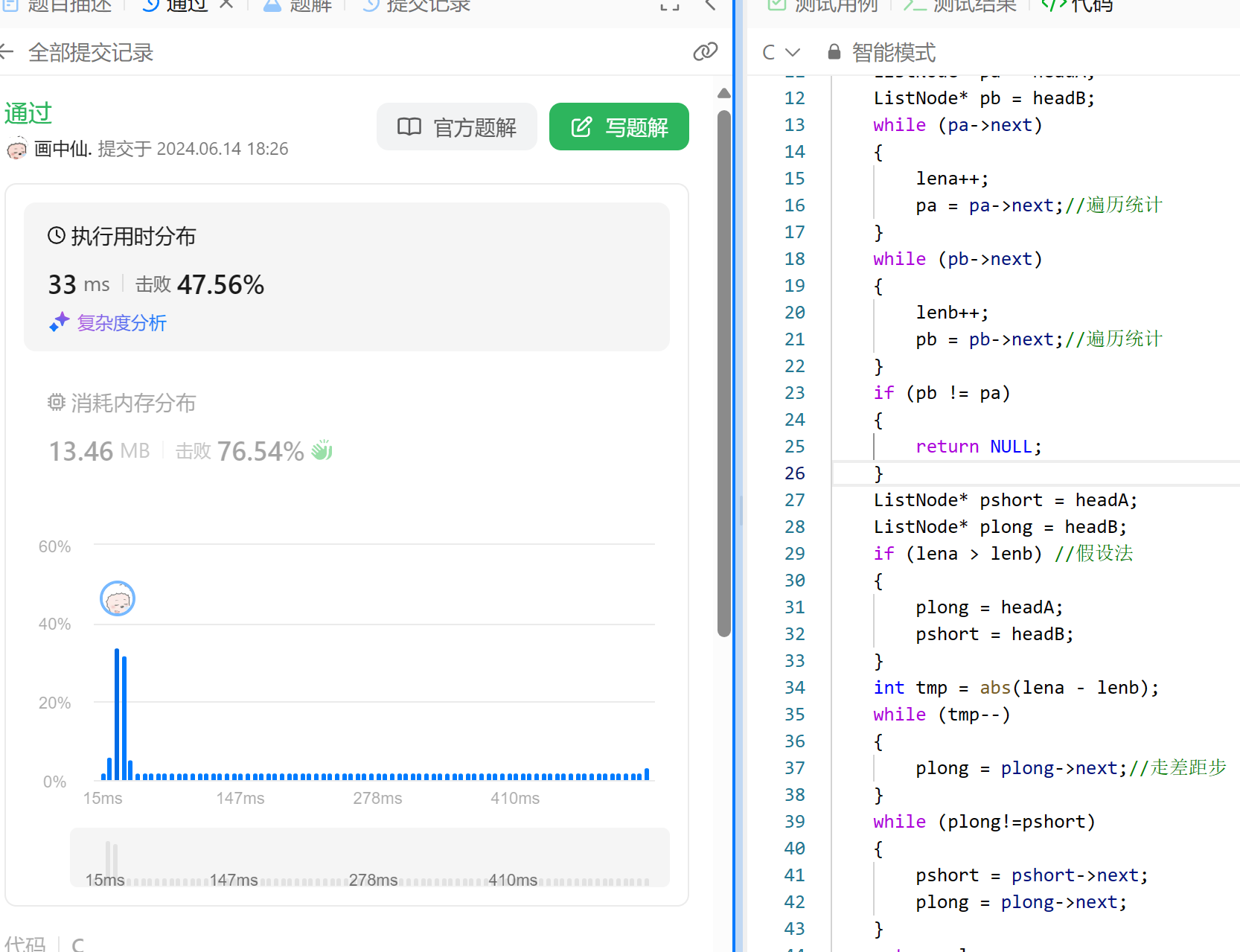
• 代码

typedef struct ListNode ListNode;
struct ListNode* getIntersectionNode(struct ListNode* headA,struct ListNode* headB) {int lena = 0, lenb = 0;ListNode* pa = headA;ListNode* pb = headB;while (pa->next){lena++;pa = pa->next;//遍历统计}while (pb->next){lenb++;pb = pb->next;//遍历统计}if (pb != pa) {return NULL;}ListNode* pshort = headA;ListNode* plong = headB;if (lena > lenb) //假设法{plong = headA;pshort = headB;}int tmp = abs(lena - lenb);while (tmp--) {plong = plong->next;//走差距步}while (plong!=pshort){pshort = pshort->next;plong = plong->next;}return plong;
}

双指针法

大家发现这些题目都会用到两个指针解决问题，这就是我们说的双指针法，具体如何运用双指针，得看具体题目灵活运用。

后言

这就是递归的复杂度和链表常见OJ。今天就分享到这里，感谢大家耐心垂阅。咱们下期见！拜拜~

这篇关于【C语言】递归复杂度与链表OJ之双指针的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---