本文主要是介绍考研计组chap2数据的表示和运算(补充),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、进位计数制

1.r进制
第i位表示r进制的权为i
2.进制转换
(1)r->10
对应位置数*权值
(2)2 -> 16 or 8
每三位2进制数可表示1位16进制
每四位2进制数可表示1位16进制
so 分开之后转为16进制即可
eg:11 1100 0010.01101转8、16
0011 1100 0010.0110 1000 => ( 3 C 2. 6 8)H
001 111 000 010.011 010 => (1 7 0 2 . 3 2)O
(3)10->2、16、18
way1:
整数部分:除r留余数
小数部分:乘r留整数
eg:123.6875->2进制
整数部分 123
123/2 = 61 ……1
61/2 = 30……1
30/2 = 15……0
15/2=7……1
7/2 =3……1
3/2=1……1
1/2=0……1
1101111
小数部分0.6875
0.6875*2=1.375
0.375*2=0.75
0.75*2=1.5
0.5*2=1
1011
so -> 110111.1011
way2:凑数
123=64+32+16+8+2+1 = 2^6+2^5+2^4+2^3+2^1+2^0=1111011
0.6875=0.5+0.125+0.0625 = 2^-1+2^-3+2^-4=.1011
so 123.6875 = 1111011.1011
3.真值和机器数
真值:人类习惯的
机器数:计算机里的样子 2 or 8 or 16进制
无符号数 or 有符号数
ATTn:计算机中数字是以补码形式存在,so运算时使用补码
二、码转制计算(binary)

1.原码
2.反码
符号位不变,数值位01互变
3.补码
反码+1
补码->原码 :way1:-1,数值位01互换
way2:数值位01互换+1
特殊:
x为定点整数,[x]补 = 1,0000000 -> x = -2^7
x为定点小数,[x]补 = 1.0000000 -> x = -1
[x]补->[-x]补 : 全01互换 +1
4.移码
补码符号位01互换,数值位不变
5.符号位+数值位
整体占机器字长n
三、加法替代减法
利用补码,-[x]补 = +[-x]补
四、0扩展、符号扩展 34
五、C语言强制类型转换 32
1.有符号数 <==> 无符号数
内容不变,直接按照规则看即可
short x = -4321;//2B=16bit// [-4321]原 = 1001 0000 1110 0001// [-4321]补 = 1110 1111 0001 1111// [y]补 = 1110 1111 0001 1111 =>[y]原->真值61,215unsigned short y = (unsigned short)x;2.长 ->短
长的部分直接截断
int a = 165537;//4B=32bit// [a]原 = 0000 0000 0000 0010 1000 0110 1010 0001 -> [a]补
// -> Ox0002 86a1(直接从IDE内存视图中获取)short b = (short)a;//2B=16bit
// ->0x86a1 -> -31071printf("b = %d\n",b);
 3.短 ->长(符号扩展)
3.短 ->长(符号扩展)
so 数值不变,仅是精度变大
(1)有符号数
符号位和数值位之间补符号数
short c =-4321;//0xef1f ->0xffff ef1fint m = x;(2)无符号数
符号位和数值位之间补0
ATTn:顶点整数在计算机中用补码存储
unsigned short q = 61215;//0xef1f -> 0x0000 ef1funsigned int p=(unsigned short ) q;六、电路补充知识——门电路
逻辑门
1.与
(1)表达式
Y = A·B = AB
(2)图形符号(只表示国际画法)(常用)

2.或
(1)表达式
Y = A+ B
(2)图形符号

3.非
(1)表达式
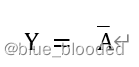
(2)图形符号

4.或非
先或后非
(1)表达式

(2)图形符号

5.异或
(1)表达式

(2)图形符号

6.同或
异或取反
(1)表达式
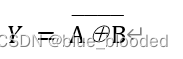
(2)图形符号

7.门变形画法
多个输入,else不变
8.三种基本逻辑运算的优先级
非 > 与 > 或
(用数学符号理解)
eg:(1) Y = AB + CD 先AB 、CD 后取或
(2)A(B+C)D 先B+C 再 A 、D
9.常见公式
(1)交换律
A(B+C) = AB+AC
(2)结合律
ABC=A(BC)
A+B+C = A+(B+C)
(3)反演律

七、加法器 (二进制)
此部分只需知道加法器(FA)的构成,标志位的名称和作用

1.一位加法器(FA)
(1)实现
一次只能计算1bit,Ai表示被加数本位,Bi表示加数本位,Ci-1表示来自低位的进位,Si表示本位和,整体利用逻辑运算进行实现
ATTn:只能进行无符号数加减
(2)Si
Si当有奇数个1时本位为1,有偶数个1时本位为0
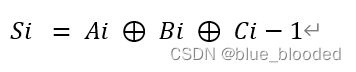
(3)Ci
至少有两个1时才能进位

(4)图形

2.带标志位的加法器 40
(1)介绍
在FA的基础上加上四个标识器,从而可以进行有符号数加减
(2)标识
1)OF(Overflow Flag)
表示带符号数是否溢出, OF = 1溢出;OF = 0不溢出
2)ZF(Zero Flag)
表示结果是否为0 ZF = 1 0;ZF = 0, 不为0
3)SF(Sign Flag)
表示结果为负or 正 SF = 1,为-,SF = 0,为+
4)CF(Carry Flag)
表示无符号数是否溢出, CF = 1溢出;CF = 0不溢出
(3)图形

1bit计算效率低,so产生两种方式:串行 or 并行
3.并行加法器(串行)
将多个FA串联
disa:后面需要等待前面运行的结果,效率也低
4.并行进位的并行加法器
(1)介绍
对并行加法器进行优化
根据数学推导,if将前面运行之后的结果一并送到后面,则效率会提高
但是if太多,则线路就会很麻烦,so一般规定4个FA并行
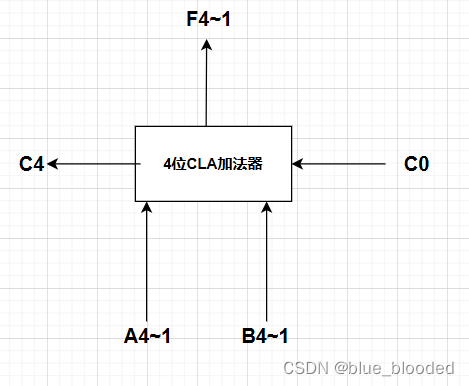
由此产生4位CLA加法器
(2)图形
八、电路知识补充——多路选择器 & 三态门
1.多路选择器
(1)作用
门卫,同时可以守多道门,只允许一个通过
(2)图形
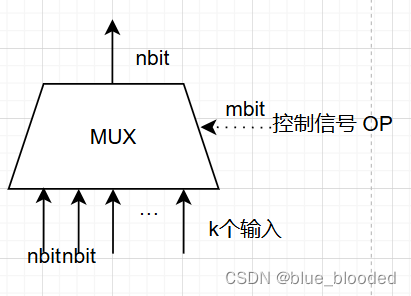
ATTn:m >= log 2 n
2.三态门
(1)作用
门卫,同时只能守一道门,决定是否通过
(2)图形
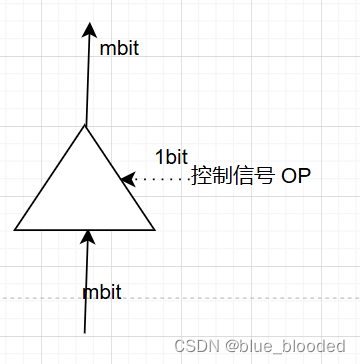
OP = 1 通过 OP = 0 不通过
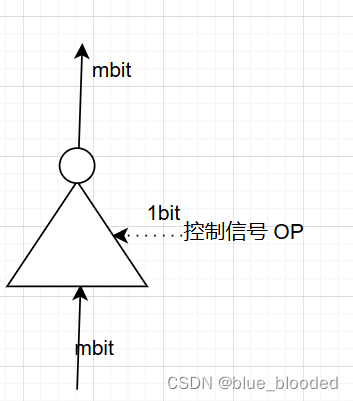
if 通过了,逐位取反之后通过
dis非门:三态门有控制信号
九、算数逻辑单元(ALU) 40

1.概念
ALU是运算器的核心,ALU的核心是(带标志的)加法器

1.功能
算数功能、逻辑功能、else
2.实现原理
加法器,四个标志,与或
3.看懂ALU图示
因为核心是加法器,so图示与加法器相似,多一个操作控制端(ALUop),选择进行什么操作,决定了ALU功能数

4.考点
(1)ifALU支持k种功能 则控制信号位数m>= log2 k up
(2)ALU的运算数、运算结果位数与计算机的机器字长相同
(3)标志位的特性
(4)标志位信息送入PSW程序状态寄存器(标志寄存器FR)
十、定点数移位运算 41

1.算术移位
当作有符号数,右移补0,左移补符号位
2.逻辑移位
当作无符号位,左右移均补0
3.循环移位
(1)不带进位位

(2)带进位位
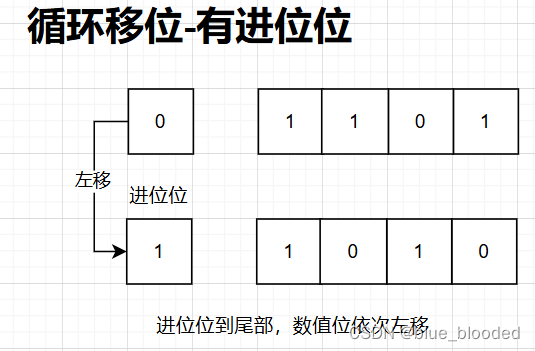
十一、定点数加减运算
1.原码 44
直接使用原码就是对应数位数值相加,可能会导致溢出
eg:1110 1111
+ 0001 0001
= 1 0000 0000 溢出了
2.补码 41
(1)计算
转为补码进行运算
x - y = x + [-y]补 所有数在计算机中以补码形式存在
x ->-x 全取反 +1
eg : 15+24 15-24 P41[x]原 = 0000 1111 = [x]补 [y]原 = 0001 1000 =[y]补[x+y ]补= 0000 1111+ 0001 1000= 0010 0111 =[x+y]原 ->真值 = +39[-y]补 = 1110 1000[x-y]补= 0001 1111+1110 1000= 1111 0111 -> [x-y]原 = 1000 1001 ->真值 -9
(2)溢出判断

way1:+++ = - 上溢 -+- = + 下溢
way2:一位符号位(模2补码),加法器中,if 本位 As、Bs 、结果位 Ss 有异号,则说明溢出
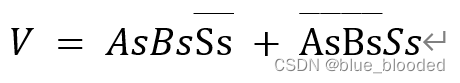
V = 0无溢出;V = 1溢出
way3:双符号位(模4补码),S1S2 == 00 结果为+,无溢出;S1S2 == 01 上溢;S1S2 == 10下溢;S1S2 == 11 结果为-,无溢出
ATTN:只存储一位符号位,运算前复制一位之后进行运算

有符号数 vs 无符号数
操作相同,way1:手算,看结果是否在正常范围内
way2:机算(溢出了):正数:最高位进1了;负数,最高位进0了
(3)补码加减的运算电路 42

十二、乘法运算
1.原码
正常小学算法中,0.1101*0.1011(二进制)
0.1101(被乘数)
*0.1011(乘数)
01101
011010
000000
01101000
= 0.10001111
看乘数的数位,为1,加被乘数;为0,不加,每次加完被乘数左移再写
(1)加法器中
ACC表示中间结果,起初全为0,MQ中存放乘数,X中存放被乘数。
eg:01101*0.1011
当乘数为1时,(ACC+01101)->(ACC)
每次加完之后ACC逻辑右移,相当于被乘数逻辑左移,so观察5次乘数尾数,右移4次后终止

(2)手算模拟
step1:先取x、y绝对值,因为是乘法,so先把符号位放着,最后确定符号位。
step2:双符号位运算
step3:符号异或(or常识)获得,数值位为ACC除了符号位+MQ中除了符号位
eg:设机器字长5位(符号位1,n = 4),x = -0.1101,y=+0.1011,求xy
step1:|x| = 00.1101 |y|= 00.1011 (原码)
step2:(如图)
step3:负数肯定符号位为1,key = 1.1000 1111

2.补码(Booth算法)
类比补码加法,使用补码进行运算,符号位参与运算,在乘数处运用辅助位(置于末尾),辅助位-数值位最低位(此处只是好记,实际上最低位是辅助位),根据正负对应+[+/-x]补,加完之后ACC算术右移,最后n次加完之后仍需判断进行+[+/-x]补,so一共n次右移,n+1次加减
(1)加法器中

(2)手算模拟
step1:转为补码
step2:符号位-最低位进行加减
step3:n次右移之后判断再+1次
step4:key为ACC+MQ除了原符号位

十三、除法运算
1.原码
小学方法:计算之后被除数-该位商*除数 ,之后补0再运算
由此可知,除法可理解为拼凑,商是找最接近被除数的除数的多少个整数倍,余数是被除数-该位商*除数的数,也就是接下来还需要拼凑的部分
(1)恢复余数法
因为二进制只会商0 or 1,so根据当时拼凑的数与除数的大小进行判断。但因为计算机设置,商默认为1,由此先减去,之后判断是否为+or-,if为-则说名商1不行,则改为0,同时因为拼凑部分-y了,需+回去,so名字为恢复余数法
eg:设机器字长5位(符号位1,n = 4),x = 0.1011,y=0.1101,求x/y
|x| = 0.1011 |y| = 0.1101 [|y|]补= 0、1101 [-|y|]补 = 1.0011
1)加法器中
在加法器中,ACC放置被除数,MQ放置商,X放置除数

2)手算模拟
step1:计算|x| = 0.1011 |y| = 0.1101 [|y|]补= 0.1101 [-|y|]补 = 1.0011
step2:商1,+[-|y|]补,检测是否正确,if拼接-除数 <0,则恢复0 且+[|y|]补
step3:计算完之后MQ、ACC左移(相当于除数右移),再取商,直到MQ位满
step4:最后检测商0是否正确,if不对还得修改
step5:最后结果 商为(MQ),余数为(ACC)*2^(-n),attn小数点的补充
3)逻辑图
(2)不恢复余数法
1)加法器中
2)手算模拟
3)逻辑图
2.补码
十四、数据的存储和排列 61
1.大端存储 vs 小段存储

c short 类型2B = 16bit,->16进制4位, 小端存储 即 倒着,so c = 0xef1f
3.字 vs 字节
32bit机器中,1字= 32bit
字节 1Byte = 8bit
4.边界对齐 vs 边界不对齐
一行1字,char(1B)占1/4字,short占半字,每半字为单位
十五、浮点数的表示与运算 55
类似科学计数法
1.浮点数的表示 55

(1)表示
1)阶码
表示次数
2)尾数
具体数值
3)真值
真正的数值
(2)规格化
1)左规
尾数算数左移,阶码-1
2)右规
尾数算数右移,阶码+1
3)原码
数值位最高位为1,具有符号位
正数:0.1xxx……x
负数:1.1xxx……x
4)补码
尾数最高数值位与符号位相反
正数:0.1xxx……x
负数:1.0xxx……x
(3)表示范围(已删除)
2.IEEE 754标准 56

(1)表示
阶码用移码表示,尾数用原码表示
移码 = 真值+偏置值
dist:在进行码之间转换时,规定偏置值为2^(n-1)
在IEEE 754中 规定偏置值为2^(n-1) -1 则float 偏置值为127
(2)data类型(eg float)
考察:float、 double、long double
阶符ms 阶码E 尾数M(隐含1.) 机器字长
1 8 23 32
(3)格式
ms;E;M ->转为16进制
(4)真值 <==>规格数
1)真值 ->IEEE 754
step:
step1:根据符号定ms
step2:整数部分和小数部分转为2进制,化为类科学计数法
step3:根据次方定E,E用移码表示----E 移码 = 真值 + 偏置值 (way2)
step4:隐藏1定M
step5:补位、组合后化为16进制
eg:十进制-8.25 ->IEEE 754 float p58
step1:
ms = 1
step2:
8D = 1000B 0.25D = 0.01B
8.25D = 1000.01B = (1.00001B)*2^3
step3:
E = [3]移码 = 10000010
way1:[3]移码=10000011 -1 = 1000010 (普通 -1)
way2:3+127=130当作无符号数 = 1000010
step4:M = 00001
step5:float 1+8+23
ms = 1 E = 10000010 M = 0000100000……0(补0到23位)
so 1;100 0001 0 ; 000 0100 0000 0000 0000 0000 -> C104 0000H
2)IEEE 754 ->真值
step:
step1:16进制化为2进制,分成ms、E、M
step2:根据ms定正负,E转为真值,M+1.
step3:组装 ->化为10进制
eg:IEEE754 C640 0000H ->真值
step1: C640 0000H-> 1100 0001 0000 0100 16个0 B
ms = 1 E = 1000 0010 M = 100 16个0
step2:ms表示负数 E = 13D
M -> 1.1B ->1.5D
step3: - 1.5* 2^13
(4)特殊值(float)
1)原因
IEEE754的偏置值为127,so -127表示全0,-128表示全1,so用作了特殊用途
2)数值
符号位表正负
i)+0 vs -0
阶码全0 ,尾数全0
ii)+∞ vs -∞
阶码全1,尾数全0
iii)无规格化正数 vs 无规格化负数
阶码全0,尾数不全为0,表示极小的正负数
iV)NAN
阶码全1,尾数不全为0
3.浮点数的运算

(1)加减运算 59
steps:
step0:转换成二进制补码(阶码和数码)step1:齐阶
用阶相减之后的正负表示大小,小->大靠拢
step2:尾数相加(减)
step3:规格化(符号位同号)
step4:舍入(末尾为0则不用舍入)
step5:判断溢出(阶次是否溢出)
step6:转为真值
eg:十进制 X = -5/256,Y = +59/1024,计算X-Y,结果用2进制表示,浮点数格式:阶符数2位,阶码位3位,数符2位,尾数9位
step0:
X = -5/256 = -101*2^(-101) Y = +59/1024 = 0.111011*2^(-100) 二进制
X : 11011,11.011000000 Y: 11100,00.111011000
step1:
11011 - 11100 = 11011 + 00100 = 11111 -> -1
X : 11011,11.011000000 -> 11100,11.1011000000
step3:
X - Y = X+ (-Y ) = 11.01100000+11.000101000 = 10.110001000
step4:
X - Y : 11100,10.110001000 右移 -> 11101,11.011000100
4.末尾为0,无舍入
5. 无溢出 真值 2^(-3)*(-0.110001)2
(1+)进行舍入分析
1)就近舍入(0舍1入)
看末尾
2)直接置1
不管末尾为0 or 1,将最后一位置1
(2)类型转换(32bit机器) 60
1)无损
char->int->long->double
float->double
2)有损
int 表示32位整数(1+31),float表示32位浮点数(1+8+23)
so int 范围 -2^31-1 ~2^31 -1,float 范围2^(-126)~1.1……1*2^(127)
int ->float 31位表示精度,float24位(1隐藏了)表示精度,so会有精度损失
float ->int 直接截断了
这篇关于考研计组chap2数据的表示和运算(补充)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!