数据结构（DS）学习笔记（4）：线性表

本文主要是介绍数据结构（DS）学习笔记（4）：线性表，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

2.1线性表的类型定义

线性表是最常用且最简单的一种数据结构，是一种典型的线性结构，一个线性表是n个数据元素的有限序列。

线性表： $(a_{1},a_{2},...,a_{i-1},a_{i},a_{i+1},...,a_{n})$ ，

$a_{1}$ —— $a_{n}$ 是数据元素， $a_{1}$ 是线性起点（起始结点）， $a_{n}$ 是线性终点（终端结点）。

$a_{i-1}$ 是 $a_{i}$ 的直接前驱， $a_{i+1}$ 是 $a_{i}$ 的直接后继。

n为元素总个数，即表长：线性表的长度。n = 0时为空表。

$a_{1}$ 是第一个数据元素， $a_{n}$ 是最后一个数据元素， $a_{i}$ 是第i个数据元素，i为数据元素 $a_{i}$ 在线性表中的位序。（位序是从1开始的，数组下标是从0开始的）

除了第一个元素外，每个元素有且仅有一个直接前趋；除了最后一个元素外，每个元素有且仅有一个直接后继。开始结点 $a_{1}$ ，没有直接前驱，仅有一个直接后继 $a_{2}$ ；终端结点 $a_{n}$ ，没有直接后继，仅有一个直接前驱 $a_{n-1}$

同一个线性表中的元素必定具有相同特征，数据元素之间的关系是线性关系。线性表中每个数据元素所占的空间是一样大的。

2.2线性表的计算

一元多项式的运算：实现两个多项式加、减、乘运算

$P_{n}(X)=P_{0}+P_{1}X+P_{2}X^{2}+...+P_{n}X^{n}$

把一元多项式中的每个系数拿出来，把他存成一个线性表，每一项的指数，用系数的下标来隐含的表示。此时系数的下标与指数相同P0常数项就是X的0次方，P₁就是X的一次方

线性表 $P=(P_{0},P_{1},P_{2},...,P_{n})$ （每一项的指数i隐含在其系数 $P_{i}$ 的序号中）

例一： $P(x)=10 + 5x - 4x^{2} + 3x^{3} +2x^{4}$ ，用数组表示：

$R_{n}(X)=P_{n}(X)+Q_{m}(X)$

线性表 $R=(p_{0}+q_{0},p_{1}+q_{1},p_{2}+q_{2},...,p_{m}+q_{m},p_{m+1},...,p_{n})$

稀疏多项式：

例一： $A(x)=7+3x+9x^{8}+5x^{17}$ $B(x)=8x+22x^{7}-9x^{8}$

$P_{n}(X)=P_{1}X^{e_{1}}+P_{2}X^{e_{2}}+...+P_{m}X^{e_{m}}$ 线性表 $P=((p_{1},e_{1}),(p_{2},e_{2}),...,(p_{m},e_{m}))$

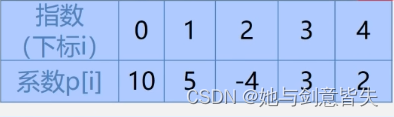
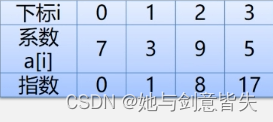
线性表A=（（7,0），（3,1），（9,8），（5,17））线性表B=（（8,1），（22,7），（-9,8））

求两个多项式的和：

（1）创建一个新的数组C

（2）分别从头遍历比较a和b的每一项：

指数相同：对应的系数相加，若其和不为零，则在C中增加一个新项；为零就不要了

指数不相同：将指数较小的项，复制到C中

（3）一个多项式已经遍历完毕时，将另一个剩余项依次复制到C中即可

所以，数组C：

思路：

1：首先比较线性表A（7,0）和线性表B（8,1），看它们的指数，一个是0一个是1，0<1，所以将线性表A的（7,0）放到数组C中（0,7）。此处线性表A（7,0）解决了，不要了。

2：因为线性表B（8,1）并没有被解决，所以接着和线性表A（3,1）比较，1=1，指数相同，系数相加3+8=11，然后放入到数组C中（1,11）。此处线性表A（3,1）和线性表B（8,1）都解决了，就不要了。

3：然后线性表A变成了（9,8）和线性表B（22,7）比较，8>7，指数不同，将线性表B（22,7）放入到数组C中（7,22）。此处数组B（22,7）解决了，不要了

4：接着看线性表A（9,8）和线性表B（-9,8），8=8，系数相加，9+(-9)=0，所以线性表A（9,8）和线性表B（-9,8）都不要了

5：此处线性表B已经没有了，线性表A还剩一项（5,17），所以直接将线性表A（5,17）复制到数组C中（17,5）

所以数组C为

顺序存储结构存在的问题：

1：存储空间不灵活 2：运算的空间复杂度高

法二：链式存储结构

$A(x)=7+3x+9x^{8}+5x^{17}$ $B(x)=8x+22x^{7}-9x^{8}$

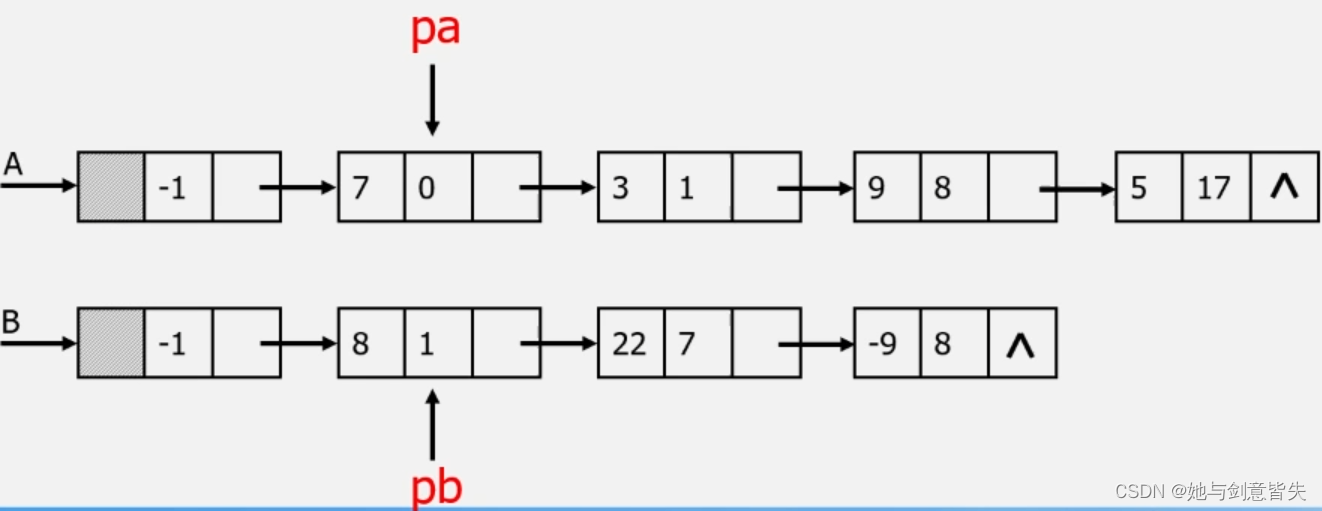首先遍历这两个多项式，A多项式第一个系数为0，B多项式第一个系数为1，0<1,所以保留0次项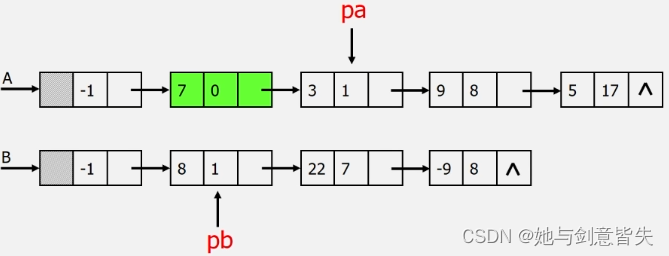

接着看A多项式第二个系数为1，B多项式第一个系数为1，1=1,然后系数相加，3+8=11

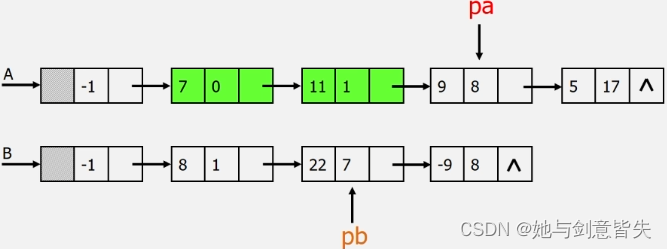
接着看A多项式第三个系数为8，B多项式第二个系数为7，7<8,所以保留这个7次项

接着看A多项式第三个系数为8，B多项式第三个系数为8，8=8,然后系数相加，9-9=0，都不要

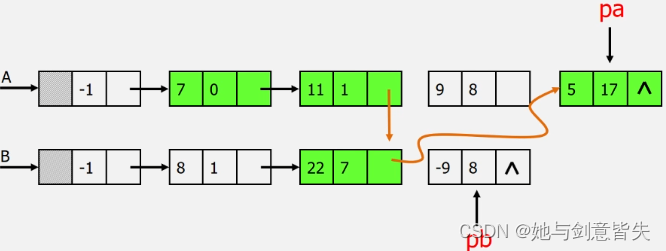
所以此方法并不需要额外空间

2.3抽象数据类型线性表的定义

ADT List{

数据对象:D = { $a_{i}$ | $a_{i}$ ∈ElemSet, i = 1,2,...,n,n≥0}

数据关系:R1 = {＜ $a_{i-1}$ ， $a_{i}$ > | $a_{i-1}$ ， $a_{i}$ ∈D, i = 1,2,...,n}

基本操作:

InitList(&L)

操作结果：构造一个空的线性表L。

DestroyList(&L)

初始条件：线性表L已存在。

操作结果：将L重置为空表。

.........

}ADT List

2.4线性表的基本操作

InitList(&L) （Initialization List：初始化线性表）

操作结果：构造一个空的线性表L。（分配内存空间）

DestroyList(&L) （删除）

初始条件：线性表L已存在。

操作结果：销毁线性表L。(从内存中删除线性表，释放空间）

ClearList(&L) （重置）

初始条件：线性表L已存在。

操作结果：将L重置为空表。（内存还有，但是没有元素）

ListEmpty(L) （判断线性表是否为空表,空表n=0）

初始条件：线性表L已存在。

操作结果：若L为空表，则返回TRUE，否则返回FALSE。

ListLength(L) （求线性表的长度：线性表当中元素的个数）

初始条件：线性表L已存在。

操作结果：返回L中数据元素个数。

GetElem(L, i, &e) (获取线性表当中元素)

初始条件:线性表L已存在,1 ≤ i ≤ ListLength(L)。

操作结果:用e返回L中第i个数据元素的值。

LocateElem(L，e，compare()) （查找、定位）

初始条件:线性表L已存在,compare()是数据元素判定函数。

操作结果:返回L中第1个与e满足关系compare()的数据元素的位序。若这样的数据元素不存在,则返回值为0。

PriorElem(L，cur_e，&pre_e) （求一个元素的前趋）

初始条件:线性表L已存在。

操作结果:若cur_e是L的数据元素,且不是第一个,则用pre_e返回它的前驱,否则操作失败，pre_e无定义。

NextElem(L，cur_e,&next_e) （获取一个元素的后继）

初始条件:线性表L已存在。

操作结果:若cur_e是L的数据元素,且不是最后一个,则用next_e返回它的后继,否则操作失败,next_e无定义。

ListInsert(&L,i,e) (插入元素)

初始条件:线性表L已存在,1 ≤ i ≤ ListLength(L)+ 1。

操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1。

例:插入元素e之前（长度为n）： $(a_{1},a_{2},...,a_{i-1},a_{i},...,a_{n})$

插入元素e之后（长度为n+1）： $(a_{1},a_{2},...,a_{i-1},e,a_{i},...,a_{n})$

此处 $a_{i}$ 是e的后继

ListDelete(&L,i，&e) （删除元素）

初始条件:线性表L已存在且非空,1 ≤ i ≤ ListLength(L)。

操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1。

例：删除前（长度为n）： $(a_{1},a_{2},...,a_{i-1},a_{i},a_{i+1},...,a_{n})$

删除后（长度为n-1）： $(a_{1},a_{2},...,a_{i-1},a_{i+1},...,a_{n})$

ListTraverse(L,visit()) （遍历线性表）

初始条件:线性表L已存在。

操作结果:依次对L的每个数据元素调用函数visit()。一旦visit()失败,则操作失败

PrintList（L）：输出：按照前后顺序输出线性表L的所有元素值。

2.5线性表的顺序表示和实现

线性表的顺序表示：顺序存储结构或顺序映象。

线性表的顺序表示：指的是用同一组地址连续的存储单元依次存储线性表的数据元素。

顺序存储定义：把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。

线性表是一种逻辑结构

线性表 $(a_{1},a_{2},...,a_{i-1},a_{i},a_{i+1},...,a_{n})$ 中，第一个元素没有前驱，最后一个元素没有后继，除了第一个元素和最后一个元素，其他元素有且仅有一个前驱和一个后继。线性表中第一个数据元素a1的存储位置，称作线性表的起始位置或基地址（首地址）。

逻辑上相邻的元素，在物理位置上也是相邻的。

例如：线性表（1,2,3,4,5,6）的存储结构是一个典型的线性表顺序存储结构。依次存储，地址连续——中间没有空出存储单元

地址不连续——中间存在空的存储单元。不是一个线性表顺序存储结构。

线性表顺序存储结构占用一片连续的存储空间。知道某个元素的存储位置就可以计算其他元素的存储位置。

2.6顺序表中元素存储位置的计算

例： $(a_{1},a_{2},...,a_{i-1},a_{i},a_{i+1},...,a_{n})$ ，如果每个元素占用8个存储单元， $a_{i}$ 存储位置是2000单元，则 $a_{i+1}$ 存储位置是？

已知每个元素占8个存储单元，所以 $a_{i}$ 占用2000~2007，这8个存储单元， $a_{i+1}$ 则是从2008开始存储的。

假设线性表的每个元素需占 $l$ 个存储单元，并以所占的第一个单元的存储地址作为数据元素的存储位置。则第 $i+1$ 个数据元素的存储位置 $LOC(a_{i+1})$ 和第 $i$ 个数据元素的存储位置 $LOC(a_{i})$ 之间满足关系： $LOC(a_{i+1})=LOC(a_{i})+l$

线性表的第 i 个数据元素 $a_{i}$ 的存储位置为： $LOC(a_{i})=LOC(a_{1})+(i-1) * l$

与数学中的等差数列相似 $a_{n}=a_{1}+(n-1)×d$ ，LOC是location的缩写。设线性表中第一个元素的存储位置是LOC（L），第二个元素的存储位置为：LOC（L）+数据元素的大小，第三个为LOC（L）+2 * 数据元素的大小

线性表顺序存储结构的图示：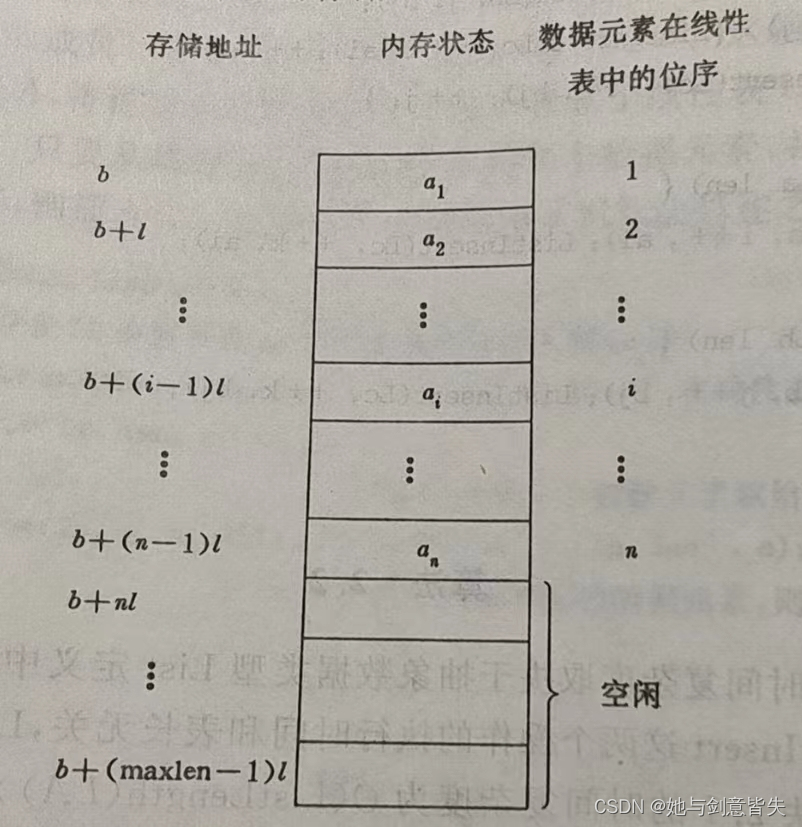

此图中的b也可以写成 $LOC(a_{1})$

2.6.1顺序表的特点

以元素在计算机内“物理位置相邻”来表示线性表中数据元素之间的逻辑关系。任意元素均可随机存取（优点）

2.6.2顺序表的顺序存储表示

线性表的长度是可以变的（删除）

一位数组的定义方式：

类型说明符数组名[常量表达式]

说明：常量表达式中可包含常量和符号常量，不能包含变量。即C语言中不允许对数组的大小作动态定义

顺序表的定义（模版）：

#define LIST_INIT_SIZE 10    //线性表存储空间的初试分配量，定义一个整型常量，值为100
typedef struct{ElemType elem[LIST_INIT_SIZE];    //用静态的“数组”存放数据元素int length;                //顺序表的当前长度
}SqList;                       //顺序表的类型定义（静态分配方式）

2.6.3多项式的顺序存储结构类型定义

$P_{n}(X)=P_{1}X^{e_{1}}+P_{2}X^{e_{2}}+...+P_{m}X^{e_{m}}$

线性表 $P=((p_{1},e_{1}),(p_{2},e_{2}),...,(p_{m},e_{m}))$

#define MAXSIZE 1000    //多项式可能达到的最大长度typedef struct{        //多项式非零项的定义float p;            //系数int   e;            //指数
}Polynomial;        //Polynomial：多项式typedef struct{Polynomialp *elem;    //存储空间的基地址int   length;        //多项式中当前项的个数
}SqList;            //多项式的顺序存储结构类型为SqList

例：图书表的顺序存储结构类型定义

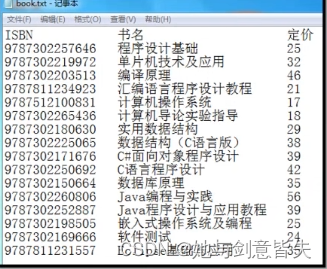
#define MAXSIZE 1000    //图书表可能达到的最大长度typedef struct{        //图书信息定义char no[20];        //图书ISBNchar name[50];        //图书名字float p;            //图书价格
}Book;        typedef struct{Book *elem;    //存储空间的基地址int   length;        //图书表当前图书个数
}SqList;            //图书表的顺序存储结构类型为SqList

2.6.4类C语言有关操作的补充

（一）补充：元素类型说明

顺序表类型定义：

typedef struct{ElemType data[];  int length;                
}SqList;                       //顺序表类型

（二）补充：数组定义

数组静态分配：

typedef struct{ElemType data[MaxSize];  int length;                
}SqList;                       //顺序表类型

数组动态分配：

typedef struct{ElemType  *data;  int length;                
}SqList;                       //顺序表类型

2.6.5顺序表的实现方式

（一）静态分配

#define MaxSize 10            //定义最大长度
typedef struct{ElemType data[MaxSize];    //用静态的“数组”存放数据元素int length;                //顺序表的当前长度
}SqList;                       //顺序表的类型定义（静态分配方式）

这篇关于数据结构（DS）学习笔记（4）：线性表的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！