本文主要是介绍数字的魅力:数学中最重要的7个常数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
数学常数是数学中一类特殊的数,具有固定不变的值。这些常数并非数学家随意凭空制定,而是源于深刻的数学原理和规律。它们不仅深刻地影响着数学理论的建立与发展,更连接着人类思维的奇妙之旅。
本文将简介数学中 7 个最基本的常数,里面每一个都有着自己的故事和意义。
0 和 1:数学的基础
首先,来看看最基本,也是最重要的两个数学常数:0 和 1,分别代表着最基本的两个概念:“无”和“有”。
0 代表着“没有数量”或“空集的势”,也是数学理论的基石。在数学的发展历史中,0 的引入是一个革命性的里程碑,是算术、代数和计数系统不可或缺的部分。
-
在代数中,0 是加法群的单位元,意味着任何数与 0 相加都会得到它自己,是组合数学和代数结构中的核心概念。
-
在解方程中,0 常常在等式和不等式解的右侧。例如,多项式的根就是使多项式等于 0 的值。
-
在度量空间中,0 是距离度量的起点。在欧几里得空间中,两点间的最短距离为 0 当且仅当这两点重合。
-
在计数系统中,特别是在我们现在使用的十进制体系中,0 是位置记数法的关键,它允许我们能区分 10 和 100 这样不同的数量级。没有 0,现代数学和科学将会非常不同——很可能发展得更晚。

1 是最小的正整数,代表了一个整数单位。1 作为人类开始计数的起点,也是在定义其他数学结构时所依赖的基础。
-
在乘法和代数结构中,1 是单位元,这意味着任何数乘以 1 都会保持不变。这个性质不仅适用于基本算术,也是更高级代数结构(如群、环和域)定义中的核心。
-
在数学归纳法中,首先证明命题在基础情况下()成立,然后假设它在 时成立,并由此证明它在 时也成立,这样逐步展示命题对所有自然数都成立。
圆周率 π:几何的核心
圆周率 π 的定义简单而深刻:周长与直径的比率。这个比值对于所有大小的圆都是恒定的,作为一个神秘而又迷人的无理数,约等于 3.14159,而后的小数位无穷无尽延续下去。

π 在数学众多分支如分析学、概率甚至在物理学中的波动和振动中起着重要作用:
-
几何学: π 不仅用于计算圆的周长 和面积 ,还用于球体的表面积 和体积 的计算。
-
分析学: π 不止出现在涉及圆的各种极限问题中,经常会以一种意想不到的方式出现,比如在莱布尼茨级数和巴塞尔问题中就有它是身影。此外,π 在复分析领域中尤为重要,它是许多积分路径和留数定理计算的关键因素。
-
概率论: 在概率论中,π 出现在正态分布的概率密度函数中,这是因为它涉及到平方的反函数,其积分需要用到 π。
-
物理学: π 在描述周期性现象中非常重要,无论是简谐振动(如弹簧振子、钟摆)还是波动(如声波、光波)。它出现在用于描述这些现象的基本公式中,例如振动的角频率公式 ,其中 是频率。

自然对数的底数 e:无处不在的增长
自然对数的底数 e 是代数和分析数学中最为重要的一个常数,约等于 2.71828。
在自然界、数学、工程、物理学以及计算机科学等多个领域都有出现。特别重要的是在于, 是唯一一个使得函数的导数(微分率)等于自身的数。
数学上, 可以通过多种方式定义,最常见的定义是利用极限:
这个定义源自基于复利增长的极限情况,描述了存款/投资随着时间增长的连续回报。更一般而言, 出现在各种自然增长或衰减过程的数学模型中,例如人口增长模型、冷却定律、或者放射性衰变等。
黄金分割比 φ:比例的魔法
黄金分割比,以希腊字母 (Phi)表示,约等于 1.61803。
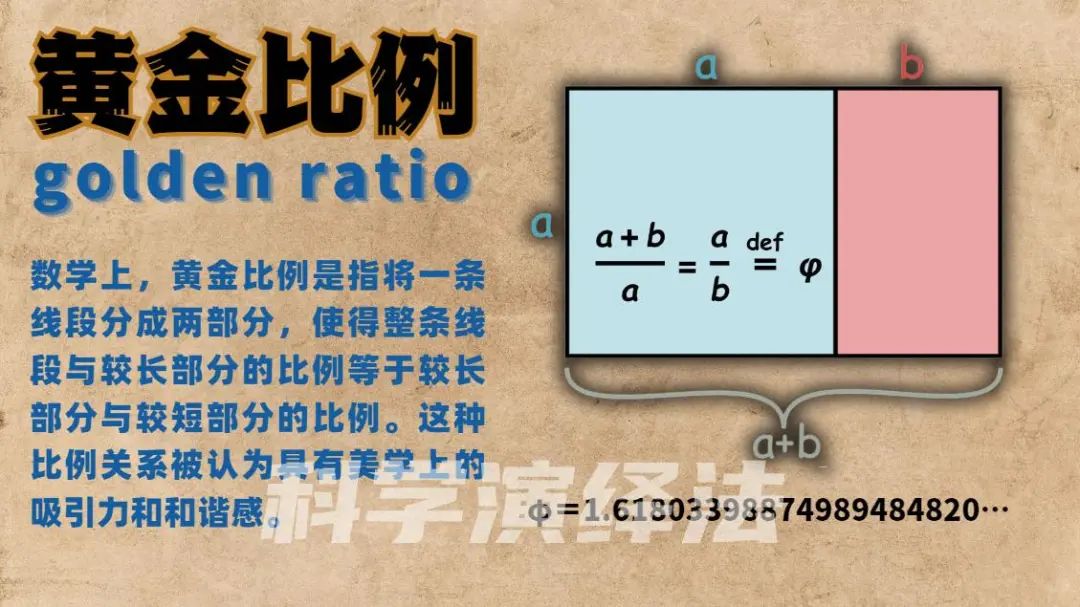
黄金分割比的定义基于一个特别的比例性质。设想一条线段,被分为两部分:较长的部分我们称之为 ,较短的部分称之为 。黄金分割比是当满足以下等式时的比例:
黄金分割比与斐波那契数列紧密相关。斐波那契数列中相邻两数的比值,随着数列的增长,其比值趋近于黄金分割比。
黄金分割在艺术和建筑设计中非常受欢迎,比被人们普遍认为最具美感的比例,而美,正是数学的另一面。
平方根 2:无理数的诞生
平方根 2,记作 ,大约等于 1.41421,是最早被认知并证明的无理数。
在几何学中, 出现在边长为 1 的正方形的对角线长度中。这个几何性质最早是由古希腊的希帕索斯发现,当时毕达哥拉斯学派最初认为所有数都可以用整数比表示,但 的发现挑战了这个信念,传说中也是因为希帕索斯颠覆了毕达哥拉斯学派关于数的理论,而被他们处以投入海中以保住这个秘密。

无理数的发现导致了实数理论的发展,因此 不仅代表了一个数字,更是整个数学体系中的一个关键节点。
虚数单位 i:复数的基础
虚数单位 是构建复数的基础,最初被引入是为了解决特定的代数问题,如方程 。在实数范围内,没有数的平方为负数,因此需要虚数的概念来解决这类问题。解为 或 。
随着虚数的引入,数学家们进一步定义了复数,这使得所有的非零单变量多项式方程都有解。这样不仅解决了实数范围内无解的问题,而且极大地扩展了数学的应用范围。

在工程和物理学领域,复数和虚数单位 的应用极为广泛。例如,在交流电路分析中,电阻、电感和电容的关系可以通过复数来表示,使得计算变得简洁。在量子力学中,复数用于描述波函数,是理论的基本组成部分。
这些常数在不同的领域有着广泛的应用,体现了数学与现实世界之间美妙的联系,简约却深刻,引领我们走向更广阔的认知边界。
这篇关于数字的魅力:数学中最重要的7个常数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







