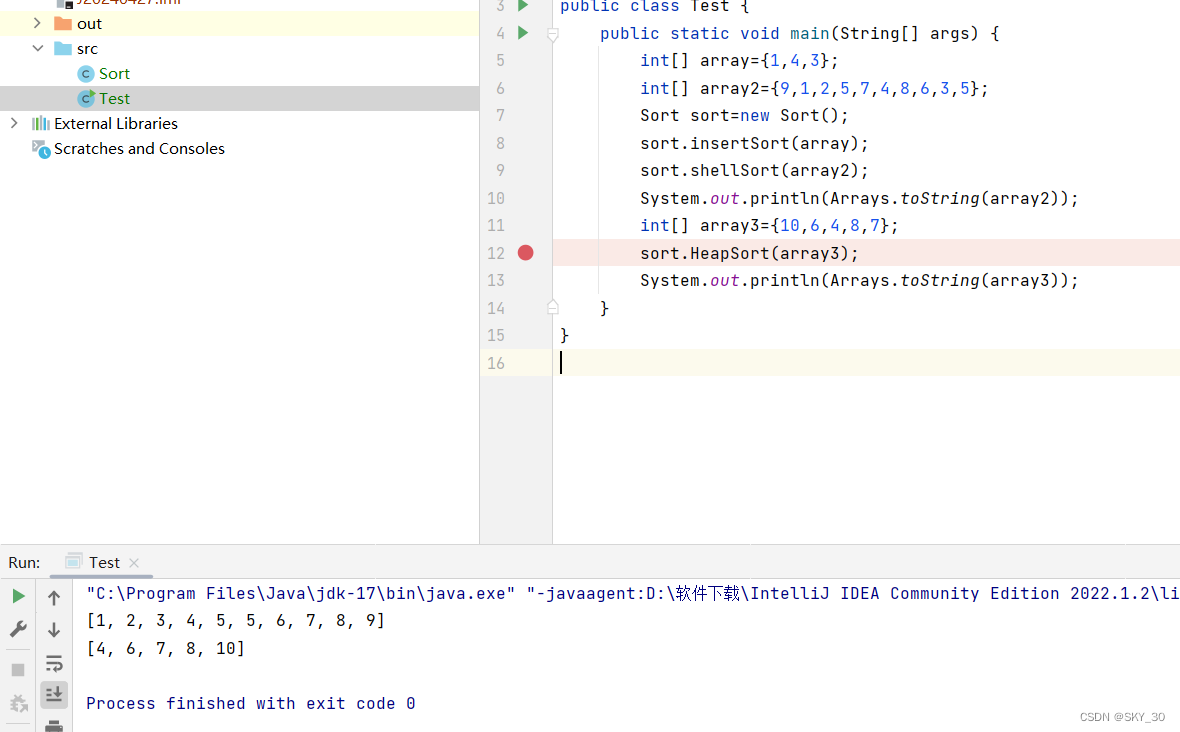
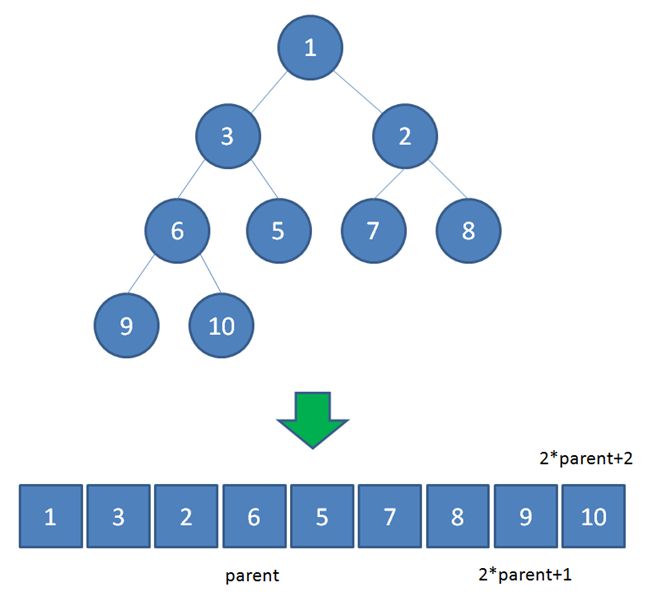
本文主要是介绍大根堆 小根堆,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转:小根堆大根堆
| 堆(Heap)分为小根堆和大根堆两种,对于一个小根堆,它是具有如下特性的一棵完全二叉树:
(1)若树根结点存在左孩子,则根结点的值(或某个域的值)小于等于左孩子结点的值(或某个域的值);
(2)若树根结点存在右孩子,则根结点的值(或某个域的值)小于等于右孩子结点的值(或某个域的值);
(3)以左、右孩子为根的子树又各是一个堆。
大根堆的定义与上述类似,只要把小于等于改为大于等于就得到了。
由堆的定义可知,若一棵完全二叉树是堆,则该树中以每个结点为根的子树也都是一个堆。
分别为一个小根堆和一个大根堆。根据堆的定义可知,堆顶结点,即整个完全二叉树的根结点,对于小根堆来说具有最小值,对于大根堆来说具有最大值。是一个小根堆,堆中的最小值为堆顶结点的值1 8。是一个大根堆,堆中的最大值为堆顶结点的值74 Q若用堆来表示优先级队列,则堆顶结点具有最高的优先级,每次做删除操作只要删除堆顶结点即可。 |
小根堆
| 定义:堆的一种,即根节点小于它的左孩子,也小于它的右孩子. 小根椎的构建: 首先,将无序序列变成完全二叉树的形式. 排序 : 然后,从最后一个叶节点的父节点开始,往前逐个检查各个节点,看其是不是符合父节点小于它的子节点,如果不小于,则将它的 子节点中最小的那个节点与父节点对换;否则,不交换,继续往前检查.直到根节点为最小节点,然后将其与最后一个节点交换.此后,继续检查各个节点是不是满足最小根要求,如果不满足,则时行调整,直到所有的节点都满足,到此,第一轮调整结束. 下一步,将上一步得到的要节点与上次交换的节点的前一个节点交换,继续和上一步一样的调整.得到第二轮调整序列. 重复上两步,直到待调整的节点个数为1. 在最小堆里插入节点: 将要插入的节点X放在原来堆的完全二叉树的最后一个位置,然后不断地往上调整,直到X 调不动为止. 。。。。。。。。。。。。。。。。。。。。。。 5、堆排序
堆排序利用了大根堆(或小根堆)堆顶记录的关键字最大(或最小)这一特征,使得在当前无序区中选取最大(或最小)关键字的记录变得简单。
(1)用大根堆排序的基本思想
① 先将初始文件R[1..n]建成一个大根堆,此堆为初始的无序区
② 再将关键字最大的记录R[1](即堆顶)和无序区的最后一个记录R[n]交换,由此得到新的无序区R[1..n-1]和有序区R[n],且满足R[1..n-1].keys≤R[n].key
③ 由于交换后新的根R[1]可能违反堆性质,故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换,由此得到新的无序区R[1..n-2]和有序区R[n-1..n],且仍满足关系R[1..n-2].keys≤R[n-1..n].keys,同样要将R[1..n-2]调整为堆。
……
直到无序区只有一个元素为止。
(2)大根堆排序算法的基本操作:
① 初始化操作:将R[1..n]构造为初始堆;
② 每一趟排序的基本操作:将当前无序区的堆顶记录R[1]和该区间的最后一个记录交换,然后将新的无序区调整为堆(亦称重建堆)。
注意:
①只需做n-1趟排序,选出较大的n-1个关键字即可以使得文件递增有序。
②用小根堆排序与利用大根堆类似,只不过其排序结果是递减有序的。堆排序和直接选择排序相反:在任何时刻,堆排序中无序区总是在有序区之前,且有序区是在原向量的尾部由后往前逐步扩大至整个向量为止。
(3)堆排序的算法:
void HeapSort(SeqIAst R)
{ //对R[1..n]进行堆排序,不妨用R[0]做暂存单元
int i;
BuildHeap(R); //将R[1-n]建成初始堆
for(i=n;i>1;i--){ //对当前无序区R[1..i]进行堆排序,共做n-1趟。
R[0]=R[1];R[1]=R[i];R[i]=R[0]; //将堆顶和堆中最后一个记录交换
Heapify(R,1,i-1); //将R[1..i-1]重新调整为堆,仅有R[1]可能违反堆性质
} //endfor
} //HeapSort |
这篇关于大根堆 小根堆的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!

![[Leetcode 230][Medium] 二叉搜索树中第 K 小的元素-大根堆/优先队列/DFS深度优先搜索](https://i-blog.csdnimg.cn/direct/52524dc6e76c4c5481612aa65567cf6d.png)