本文主要是介绍【建议收藏】一些关于鸿蒙HarmonyOS求职面试内容总结与分享,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
据介绍,目前鸿蒙系统已运行在众多全场景设备。未来,HarmonyOS将向下扎到根,全面突破操作系统内核、AI大模型、AI框架和编译器、编程语言等核心技术,为生态建设打下坚实底座。目前已面向开发者开放申请的鸿蒙星河版,将打造原生精致、原生易用、原生流畅、原生安全、原生智能、原生互联等极致体验。
最近接到了一些公司的入职面试邀约,这里略去公司的和项目的名字,做一些整理分享。
一、长列表如何实现部分渲染,使用的是哪一个API
在鸿蒙系统中,可以使用List组件来实现长列表的部分渲染。List组件支持使用条件渲染、循环渲染、懒加载等渲染控制方式生成子组件。
当列表内容较多时,可以使用懒加载来提高性能。通过按需迭代加载数据并创建相应组件,可以减少页面启动时间和服务器压力。
具体实现方式可以参考鸿蒙开发指南或相关文档。
二、对加密算法的了解,如AES等
加密算法是用于保护信息安全的重要技术。
AES(Advanced Encryption Standard,高级加密标准)是一种广泛使用的对称加密算法。它具有以下特点:
安全性高:经过了严格的分析和验证。
效率较高:加密和解密速度相对较快。
广泛应用:在许多领域如网络通信、数据存储等得到应用。
对称加密算法的特点是加密和解密使用相同的密钥。AES 支持不同的密钥长度,如 128 位、192 位和 256 位,密钥长度越长,安全性通常越高。
除了 AES 之外,还有其他一些加密算法:
DES(Data Encryption Standard):曾经是重要的标准,但现在安全性相对较低。
RSA:一种非对称加密算法,用于密钥交换等。
加密算法在保障信息机密性、完整性和不可否认性方面发挥着关键作用,对于保护个人隐私、企业数据和国家安全都具有重要意义。它们可以防止未经授权的访问、篡改和窃取信息。
思路补充:
可以讲到调用加密器接口,预先准备容器存放两组数据,首相将预设的密码、信息等数据通过加密的形式持久化存储在本地或远端服务器。之后在输入密码、秘钥时,通过同样的加密工具进行对称加密,将加密后得出的码值进行对比,对比正确时即通过验证,可以打开密码、获取加密信息。
三、对UIAbility的了解
UIAbility是鸿蒙系统中一种包含用户界面的应用组件,用于与用户进行交互。每个 UIAbility 组件实例对应最近任务列表中的一个任务,可以包含多个页面来实现不同功能模块。为了使用 UIAbility,需要在module.json5配置文件的abilities标签中声明其相关信息,包括名称、入口、描述、图标等。
UIAbility 组件的生命周期包括四个状态:Create、Foreground、Background和Destroy。在不同状态之间转换时,系统会调用相应的生命周期回调函数。在Create状态下,可以进行应用初始化操作,如变量定义、资源加载等。在WindowStageCreate和WindowStageDestroy状态下,可以进行 UI 界面的设置和事件订阅。
一个 UIAbility 可以对应多个页面,建议将一个独立的功能模块放到一个 UIAbility 中,以多页面的形式呈现。在 UIAbility 内页面的跳转和数据传递方面,可以通过新建多个页面来实现和丰富应用的内容。
四、对封装的经验与认识,举例说明
通过将按钮的功能和样式封装在一个自定义组件中,我们可以在不同的地方重复使用这个组件,而无需每次都重新创建和设置按钮的属性。这样可以提高代码的复用性和可维护性,使代码更加简洁和易于管理。
扩展思路:举例,如http方法的封装、SQLLite数据库查询方法的封装等
五、对断点续传的认识
在鸿蒙中,断点续传是一种在数据传输过程中很有用的机制。
以下是对其的一些认识:
断点续传允许在传输中断(如网络故障、设备异常等情况)后,恢复传输时从上次中断的位置继续进行,而不是从头开始。这可以极大地节省时间和资源,提高数据传输的效率和可靠性。
实现断点续传通常需要记录上次传输的进度信息,比如已传输的数据量或文件位置等。在鸿蒙系统中,可能会通过一些特定的数据存储方式或与网络通信相关的机制来管理这些进度信息。
在实际应用中,比如文件下载等场景,断点续传能为用户带来更好的体验,避免因意外情况导致的重复操作。它也体现了系统在数据传输方面的灵活性和智能性。
六、对并发的认识
在鸿蒙系统中,对并发的认识如下:
并发意味着系统可以同时处理多个任务或操作。在鸿蒙系统中,并发能力可以体现在多个方面。
从应用开发角度来看,开发者可以创建多个线程或进程来执行不同的任务,这些任务可以同时运行,提高系统的整体效率和响应速度。例如,可以同时进行数据处理、网络通信、界面渲染等操作,而不会相互阻塞。
鸿蒙系统本身也需要在底层很好地处理并发情况,以确保各个组件和服务能够高效协同工作。这包括对系统资源的合理分配和调度,避免并发冲突导致的错误或性能下降。
在多设备互联场景中,并发更是至关重要,多个设备之间的数据交互和协同操作需要在并发环境下准确、有序地进行。
同时,在处理并发时需要注意线程安全、资源竞争等问题,通过合适的同步机制和设计模式来保障系统的稳定性和正确性。总之,并发是鸿蒙系统实现高效运行和强大功能的重要支撑之一。
补充:提及async … await 、Promise等方法
七、如何使用鸿蒙语言实现饼图的设计
在鸿蒙系统中,可以使用 ArkTS 语言来实现饼图的设计。以下是一个简单的示例代码,演示如何使用 ArkTS 创建饼图:
import { Chart } from '@ohos.charts';
// 创建饼图
const pieChart = new Chart.Chart({type: 'pie',width: 300,height: 300,data: [{ value: 20, color: '#ff0000' },{ value: 40, color: '#00ff00' },{ value: 60, color: '#0000ff' },],
});
// 添加饼图到页面
pageContext.add(pieChart);
在上述代码中,首先创建了一个饼图对象pieChart,通过设置type属性为pie来指定饼图类型。然后,设置饼图的宽度、高度和数据。数据是一个数组,每个元素包含一个对象,其中value属性表示饼图的百分比值,color属性表示饼图的颜色。
最后,使用pageContext.add(pieChart)方法将饼图添加到页面中。
请注意,这只是一个简单的示例,实际的饼图设计可能需要更多的配置和样式设置。你可以根据具体需求进一步修改和扩展代码。
八、路由跳转的相关知识,包括路由跳转的层次、路由跳转的框架、路由跳转的过滤等
在鸿蒙系统中,路由跳转可以通过页面路由(Router)机制来实现。页面路由是一种用于在不同页面之间进行切换的机制,可以通过配置路由规则和使用路由组件来实现路由跳转。
鸿蒙系统的路由跳转框架提供了两种跳转模式:router.pushNamedRoute()和router.replaceNamedRoute()。这两种模式决定了目标页是否会替换当前页。router.pushNamedRoute():目标页不会替换当前页,而是压入页面栈。这样可以保留当前页的状态,并且可以通过返回键或者调用router.back()方法返回到当前页。router.replaceNamedRoute():目标页会替换当前页,并销毁当前页。这样可以释放当前页的资源,并且无法返回到当前页。
同时,Router 模块提供了两种实例模式,分别是 Standard 和 Single。这两种模式决定了目标 url 是否会对应多个实例。Standard:标准实例模式,也是默认情况下的实例模式。每次调用该方法都会新建一个目标页,并压入栈顶。Single:单实例模式。即如果目标页的 url 在页面栈中已经存在同 url 页面,则离栈顶最近的同 url 页面会被移动到栈顶,并重新加载;如果目标页的 url 在页面栈中不存在同 url 页面,则按照标准模式跳转。
在使用页面路由 Router 相关功能之前,需要在代码中先导入 Router 模块。import { router } from ‘@kit.ArkUI’。
总结
有很多小伙伴不知道该从哪里开始学习鸿蒙开发技术?也不知道鸿蒙开发该重点掌握的又有哪些?自学时频繁踩坑,导致浪费大量时间。结果还是一知半解。所以有一份实用的鸿蒙(HarmonyOS NEXT)全栈开发资料用来跟着学习是非常有必要的。
这份鸿蒙(HarmonyOS NEXT)资料包含了鸿蒙开发必掌握的核心知识要点,内容包含了
最新鸿蒙全栈开发学习线路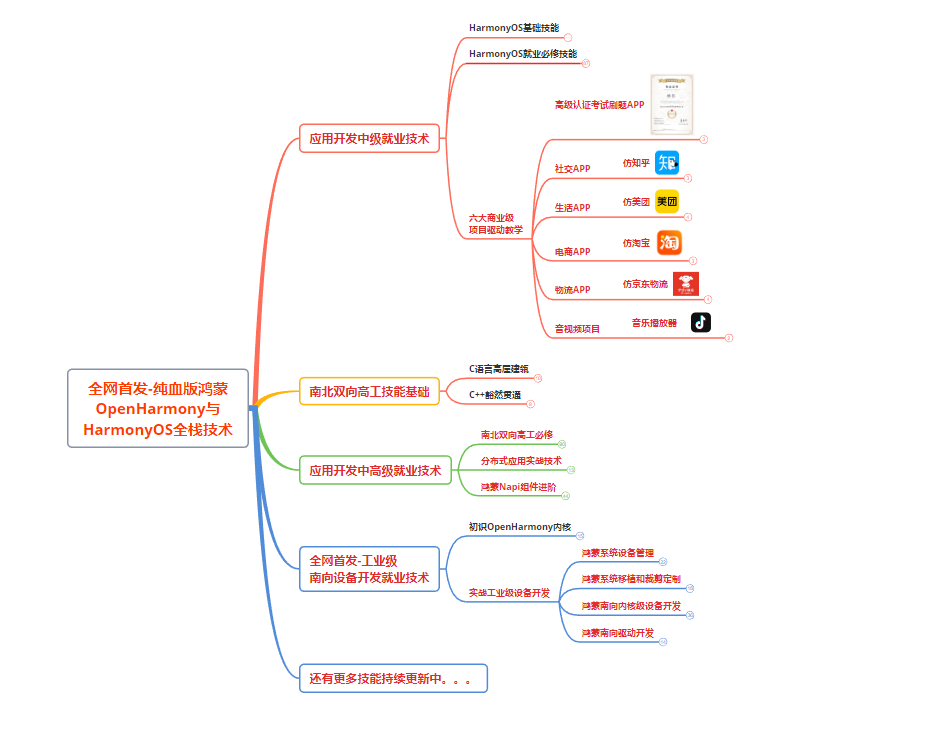
鸿蒙HarmonyOS开发教学视频
大厂面试真题


鸿蒙HarmonyOS源码剖析
这份资料能帮住各位小伙伴理清自己的学习思路,更加快捷有效的掌握鸿蒙开发的各种知识。有需要的小伙伴自行领取,,先到先得~无套路领取!!
获取这份完整版高清学习路线,请点击→[鸿蒙全栈开发学习资料]

这篇关于【建议收藏】一些关于鸿蒙HarmonyOS求职面试内容总结与分享的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






