本文主要是介绍振动分析-2-信号频域分析以及频率分辨率的理解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考2023-11-26 什么是频率?
参考2016-10-31什么是固有频率?
参考2024-01-28什么是频率分辨率?
参考2024-01-07香农采样定理有两种描述,哪个正确?
1 什么是频率
1.1 频率的定义
我们把振动发生完成一个完整往复循环所需要的时间称为周期,用符号 T 表示,单位为 s ;把一秒钟内完成往复循环振动的次数称为频率,用符号 f 表示,以Hz为单位,可记作1/秒(s-1)。
1.2 频率的分类
1.2.1 固有频率
结构系统在受到外界激励产生响应时,将按特定频率发生自然振动,这个特定频率被称为结构的固有频率,通常一个结构有很多阶固有频率。固有频率由系统本身的质量分布与刚度分布决定,与外界激励没有关系。
对于一般性结构系统而言,都是有阻尼的,因此它的固有频率为有阻尼固有频率。
为什么存在多阶固有频率?

1.2.2 基频和主频
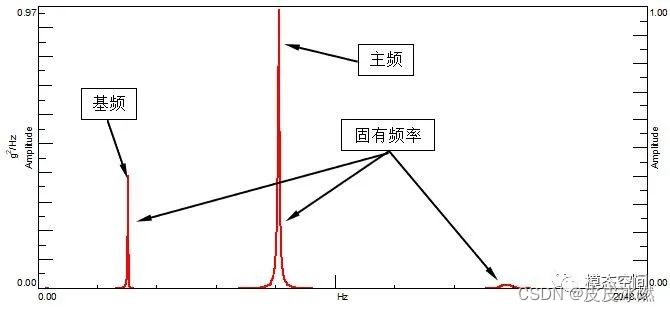
通常,将结构系统的第1阶固有频率称为基频。结构发生振动时,通常不会是按某一个频率振动,而是有多个振动频率,在这些振动频率中,能量最大的振动频率称为主频。因此,这个主频可能是结构的固有频率,也可能是强迫响应频率(外界的激励频率)。
如图3所示的功率谱密度(PSD)曲线中,存在3个峰值,假设都是固有频率,最低阶的固有频率为基频,峰值最高的频率为主频。由于主频主要看的是能量大小,所以,主频不一定是结构的固有频率,有可能是强迫响应频率。
1.2.3 共振频率
当外界激励频率与系统的某一阶固有频率相同或者非常接近时,系统将产生大幅度的振动响应,这种现象称之为共振,共振发生时的频率称为共振频率。
由于结构存在多阶固有频率,因而,结构的共振频率也有多个。不管共振是否发生,结构的固有频率是不变的,而只有当外界的激励频率接近或等于系统的固有频率时,系统才出现共振现象。因而,共振频率不一定完全与固有频率相等,共振频率是按外界的激励频率来讲的,而固有频率是从结构属性来讲的。虽然很多情况下,都认为共振频率就是固有频率。但是,二者还是有明显的差异。
1.2.4 谐波
有些振动,如弦振动、密闭房间的声腔模态或发动机的燃烧,会产生多个相关的频率。这些相关的频率成分称为激励的主要频率成分的“谐波”,而激励的主要频率成分称为“基频”。
谐波是指对周期性非正弦信号进行傅里叶变换所得到的大于基频的各次分量,通常称为高次谐波。谐波的频率等于基频的整数倍,如基频3倍的波称之为三次谐波,基频5倍的波称之为五次谐波,以此类推。不管几次谐波,他们都是正弦波。
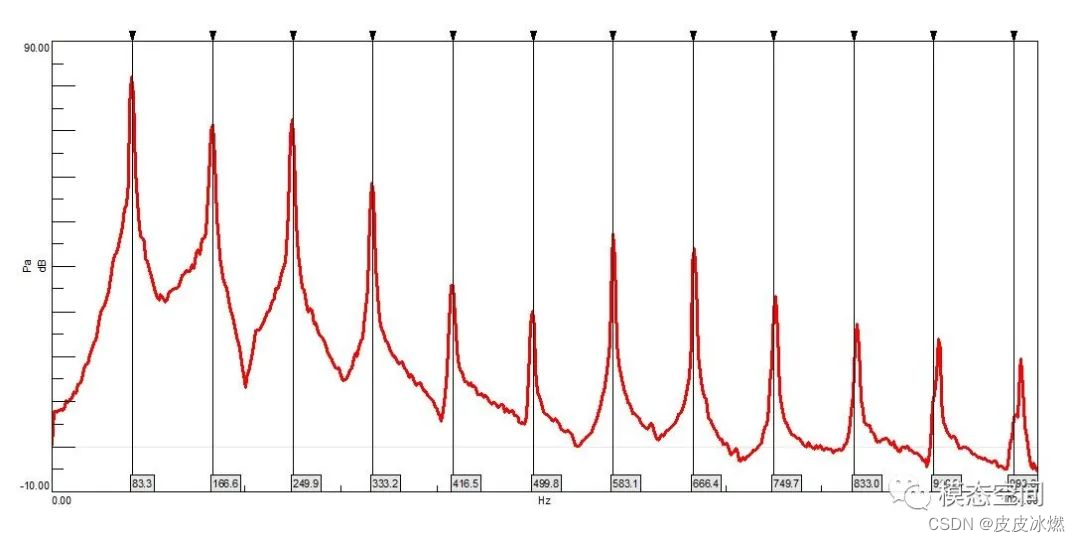
基频整数倍的谐波也称为谐波分量。谐波分量在频域的频率成分称为谐频或倍频,如图4所示为琴弦基频833Hz的各个谐频成分。
1.2.5 工频
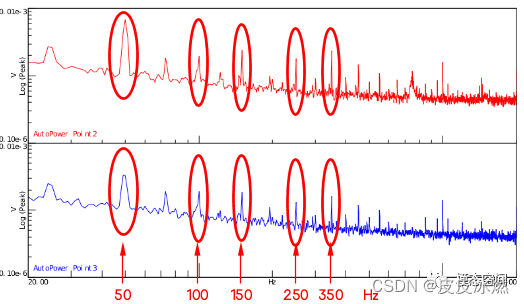
我国使用的生活用电是一种频率为50Hz的正弦交流电,交流电的频率,工业上称之为工频。在全世界的电力系统中,工频有两种,一种为50Hz,另一种是60Hz。在信号采集过程中经常会出现工频干扰,从频域看信号的频率成分为50Hz及它的倍频,如图5所示。工频来源可能是供电的市电、发电机、电动机、泵、供电设备、日光灯、电磁场等。
1.2.6 转频
对于旋转机械而言,转速(角速度)是一个非常重要的参数。
转速表示每分钟旋转的圈数,单位为rpm(Revolution Per Minute)。
如果用每秒钟旋转的圈数来表示,则称为转动频率,简称为转频,是频率的一种表现形式。也就是说转频与转速的关系如下:
转频=转速/60
1.3 与阶次的区别与联系
对于常规的振动(线振动)而言,振动频率是2Hz,或者说每一秒钟时间振动这个事件发生的次数是2次。
对于扭转振动(角振动)而言,通常用阶次这个名词来描述,阶次表示的是旋转部件每旋转一圈(360度)振动这个事件发生的次数。
线性振动 频率与时间
扭转振动 阶次与圈数
阶次的物理意义是表示每圈事件发生的次数。
阶次是表示每圈事件发生的次数,而转频是表示每秒钟旋转的圈数。
那么,阶次对应的事件的频率则是阶次乘以转频。
1阶次对应的事件的频率是1倍的转频,
k阶次对应的事件的频率是k倍的转频,或者说1阶次对应的频率是1倍转频,k阶次对应的频率是k倍转频。不管转速如何变化,这种关系都是固定不变的,因此,我们说阶次独立于转速。
1.4 信号的频率成分
1.4.1 宽(频)带信号
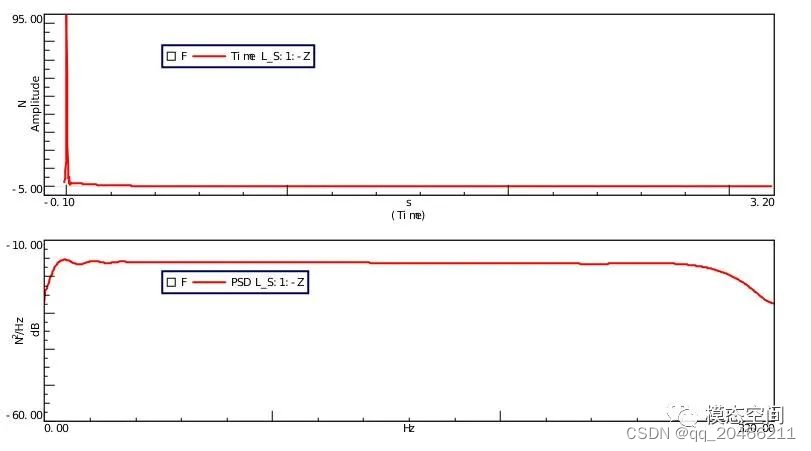
信号的频率成分分布或宽或窄,若信号频率分布很广(信号频率成分是连续的),可以认为是一个宽(频)带信号,如白噪声。对于锤击法而言,则是一种宽带激励技术,这是因为力脉冲对应的力谱是一个连续的宽频信号,能激起很宽的频率范围内的模态,如图所示,上图为力脉冲时域波形,下图为力的PSD,从下图可以看出,力谱是一个宽频信号。通常,在时域窄的信号,在频域有宽的频率分布。
1.4.2 窄(频)带信号
与宽带信号相对应的是窄(频)带信号,假设信号的频率宽度为B,中心频率为 f0,如图9所示。通常认为窄带信号满足以下要求:信号的频率宽度B远小于中心频率f0,通常要求B/f0<0.1 。例如,单频信号属于窄带信号,以及我们大多数情况下测量的信号只包含若干个单频成分,那么这也是窄带信号,对应的频谱称为窄带谱(用若干谱线表示)。如使用步进正弦进行激励时,则这种激励技术是一种窄带激励技术,因为每一时刻,激励信号只有一个单频成分。
另外,也可以从频率成分来理解宽带与窄带,若信号相邻频率成分相差很小,则可认为是一个宽带信号,如宽带随机信号;若相邻频率成分相差甚远,则属于窄带信号,如正弦信号。
若信号只有一个频率成分,则称为单频信号,如正弦信号。单频信号是窄带信号的一种特殊形式。只包含单一频率成分的声音,称为纯音。
通常,我们测试的信号的频率成分不会简简单单地只有一个单频成分,更多的是由多个频率,或有限数目相关的谐波,或无限数目不相关的单频成分组成。如图10所示,我们可以把信号的频率成分分成以下四种情况:
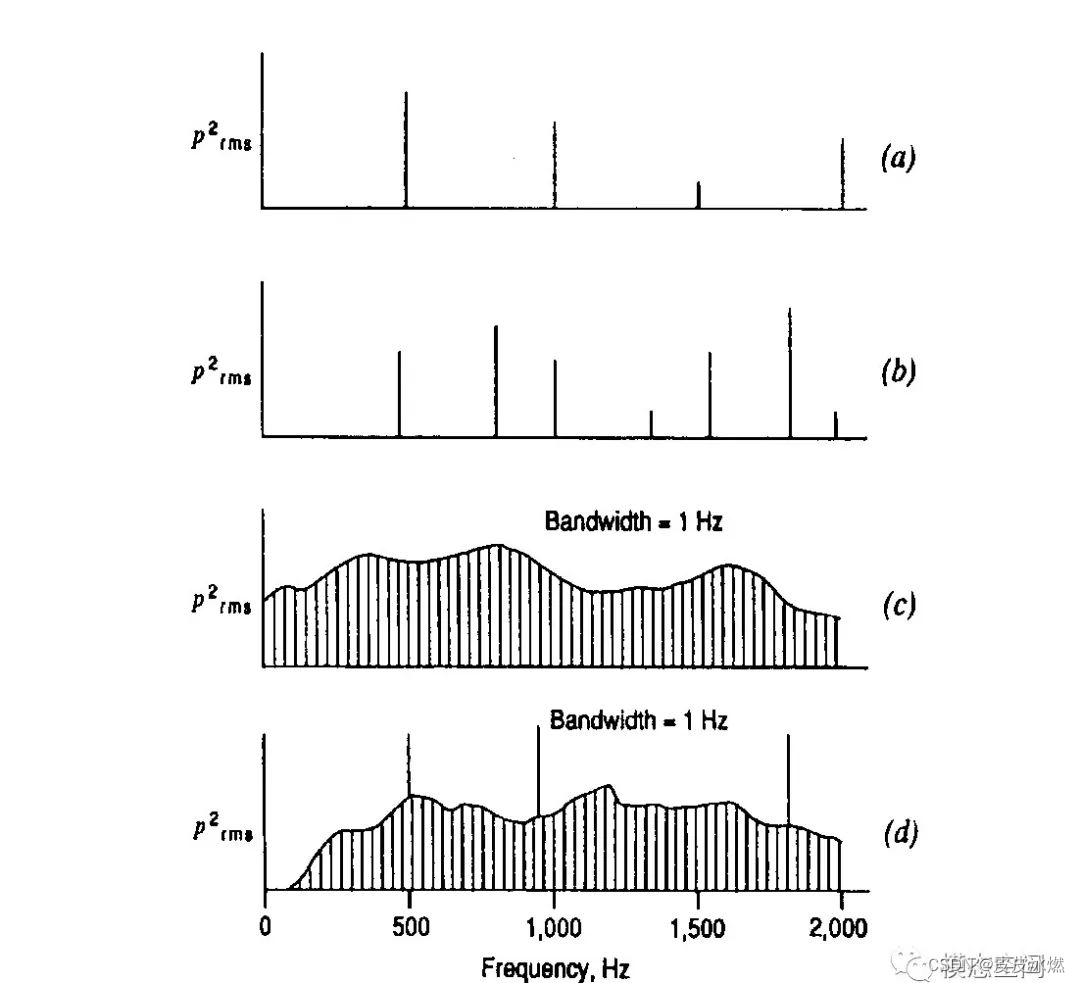
(a)有限数目的谐波成分,如在某个固定转速下变速箱的啸叫。啸叫声为某级定轴齿轮对的啮合频率以及其倍频。
(b)有限数目的非谐波成分,当传动装置存在多个传动路时,就会存在多个齿轮对,每个齿轮对都可能出现啸叫声,并且还有相应的倍频成分。
©无限频率成分的连续谱,这种频率成分类似随机噪声,包括所有的频率成分,并且无主要的频率成分,如路噪就属于这种情况。
(d)复杂频谱:既有若干单频成分,又有连续的频谱,也就是说既有随机噪声,又存在一些主要的单频成分,如车内噪声和飞机噪声就属于这种情况。
1.5 频率测量方法
早期,测量设备欠发达,测量单频信号的频率成分时有与标准频率比较的拍频法、频闪法,以及利用稳定的李萨如图判定频率的示波器法和频率计等测量方法。这些方法测量测量频率单一,精度差,在今天,都已不常用。
现今,普遍采用数据采集设备对模拟信号进行采样,获得数字信号后,再利用快速傅立叶变换(FFT)确定信号的频率成分,该方法可以确定信号复杂的频率成分,且利用计算机处理,可边测边显示频率成分,高效便捷、显示方便。
获得数字化信号最普遍的形式是使用等时间采样。也就是数据是按恒定的采样率进行采样。在满足香农采样定理前提条件下,采样后的信号将不存在频率混叠,采样后的信号是有效的数字化信号x(t)。如果我们对这个信号x(t)进行快速傅立叶分析,那么,将得到这个信号在不同频率处的频率分量,如图11所示。
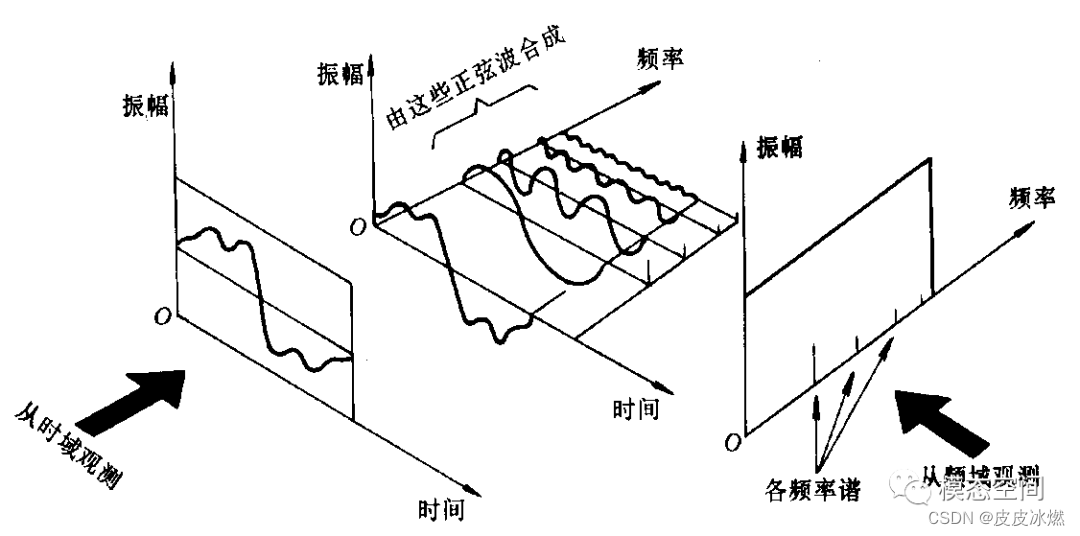
使用数据采集设备进行采样获得时域数字信号,是图中从时域观测到的时域信号,对这个采集到的时域信号进行FFT变换,相当是对这个时域信号进行分解,分解成一系列不同幅值和频率的正弦波或余弦波,图中的时域信号是4个正弦波的组合,每个正弦波或余弦波使用一条谱线就可以描述,因此,当从频域观测时,可以看到,图示的信号有4条幅值不同的线状谱,对应图中间的4个正弦波的频率成分和幅值。因此,FFT变换是将信号从时域变换到频域,告诉我们信号具有哪些频率成分。某次实际测量的振动信号的频谱如图12所示。
这个变换过程完全是可逆的。也就是说,如果我们有信号x(t),我们能通过FFT变换得到X(f)。类似地,如果我们有信号X(f),也可以通过IFT(傅立叶逆变换)变换能得到x(t)。有时,这个过程可以写成如下形式:
x(t)<——>X(f)
以上变换过程,从理论上讲是可能的,但从现实角度来讲,FFT变换过程存在泄漏,而IFT变换过程存在逆泄漏,因此,变换后总会丢失一些信息,使之与变换前存在明显差异。
2 什么是频率分辨率
什么是机械振动?
什么是扭转振动?
什么是共振?
什么是阻尼?
什么是相位?
什么是域?如时域、频域、拉氏域等
什么是混叠?
什么是瀑布图分析
2016-11-14什么是阶次?
2017-10-08怎么理解阶次?
怎样求信号中的RMS值?
什么是倍频程?
怎么看频谱图?
信号频域分析方法的理解(频谱、能量谱、功率谱、倒频谱)
什么是分贝dB?
带宽、谱线数和频率分辨率有内在关系。确定其中任一两个参数,第3个随之确定。
2.1 频率分辨率的定义

一帧数据长度 由左上角的0.5s增加到左下角的1s,则频率分辨率由右上角的2Hz减少为右下角的1Hz。频率分辨率数值更小,谱线更密,频率精确更高。
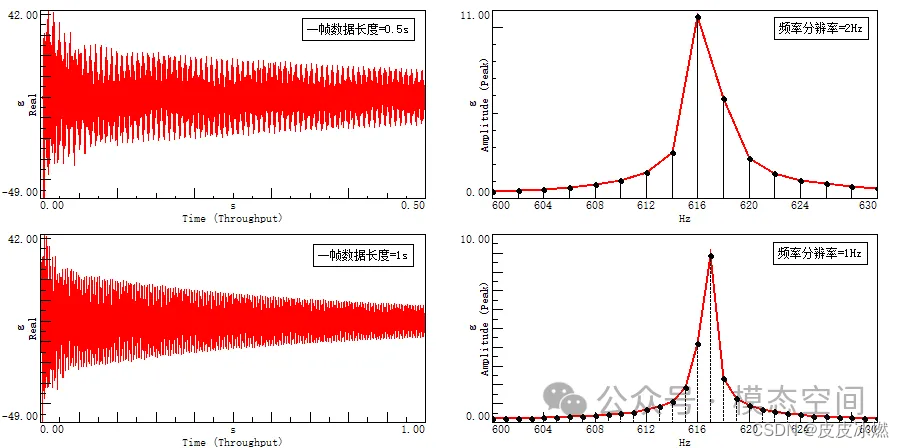
一次FFT分析N个数据点,那么,得到的频谱图有N/2条谱线。

这是因为带宽B是采样频率的一半。

上式表明,带宽、谱线数和频率分辨率有内在关系。确定其中任一两个参数,第3个随之确定。
2.2 对频率精度的影响(栅栏效应)
FFT计算结果只位于各条谱线处,谱线与谱线之间是没有结果的,频谱的这种离散效应,称为栅栏效应。
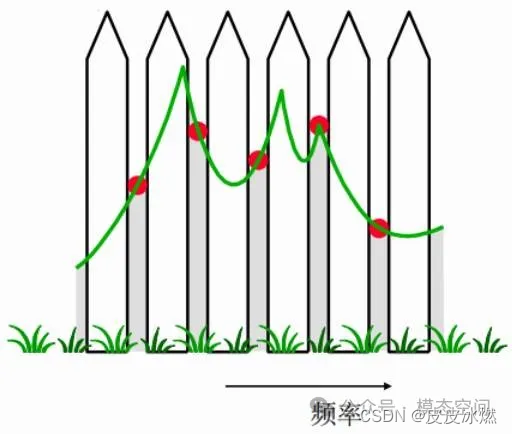
频率分辨率数值越小,相邻谱线间隔越近,求得的频率误差越小,频率精度越高。但是另一方面,这要求截取更长的一帧时域信号。
2.3 对幅值的影响(拖尾效应)
得到的频谱,除了频率存在误差之外,信号的幅值也不准确,频谱出现明显的拖尾效应。
20Hz正弦信号在频率分辨率1.6Hz下的频谱:
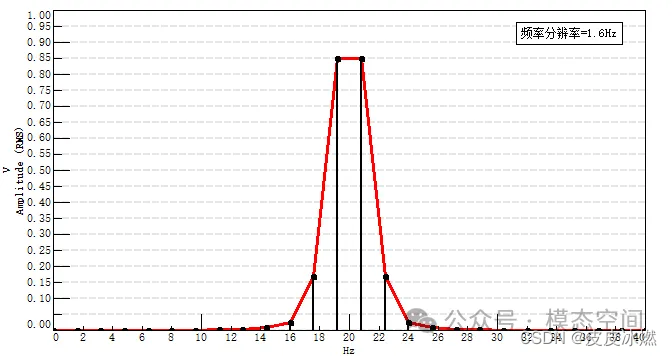
频谱由单条谱线变成了能量主要分布到4条谱线上,因此,出现了明显的频谱拖尾效应。
在带宽一定的情况下,不同的频率分辨率使得频谱具有不同的谱线数。随机信号的总能量要分布到每条谱线上,随着谱线数量的增加,每条谱线上的幅值必然降低。
这篇关于振动分析-2-信号频域分析以及频率分辨率的理解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






