Caffe源码阅读（3）Softmax层和SoftmaxLoss层

2024-06-11 04:48
文章标签 源码 阅读 caffe softmax softmaxloss

本文主要是介绍Caffe源码阅读（3）Softmax层和SoftmaxLoss层，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！


Reference Link:
http://zhangliliang.com/2015/05/27/about-caffe-code-softmax-loss-layer/

关于softmax回归

看过最清晰的关于softmax回归的文档来源自UFLDL，简单摘录如下。
softmax用于多分类问题，比如0-9的数字识别，共有10个输出，而且这10个输出的概率和加起来应该为1，所以可以用一个softmax操作归一化这10个输出。进一步一般化，假如共有k个输出，softmax的假设可以形式化表示为：

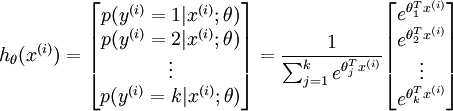
然后给这个假设定义一个loss function，就是softmax回归的loss function咯，形式化如下：

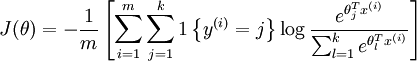
也很直观，对于某个样本i，他对应的gt label是j，那么对于loss function来说，显然只需要关心第k路是否是一个概率很大的值，所以就用一个l{·}的示性函数来表示只关心第 y(i) y(i)路(即label对应的那一路)，其他路都忽略为0。然后log的部分其实就是第k路的概率值取log。最后需要注意到前面还有一个负号。
所以总的来说，这个loss function的意思是说，对于某个样本，我只看他gt对应的那个路子输出的概率，然后取一个-log从最大化概率变成最小化能量。
然后softmax可以求梯度，梯度的公式是：

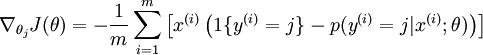
然后在实际应用中，一般还是要加上一个正则项，或者在UFLDL教程中被称为权重衰减项，于是loss function和回传梯度都多出了一项，变成了：


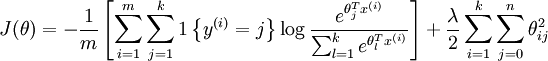
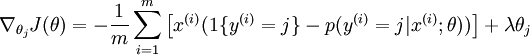
然后softmax回归就介绍完了，感觉不懂的话具体还是看UFLDL的教程比较好。

Caffe中的实现

注意这里贴的代码是基于笔者所使用的caffe版本的，大概是2015年初的吧，跟目前的最新caffe版本可能有所出入。
在实现细节上，train时候在最后接上SoftmaxWithLossLayer，test的时候换成SoftmaxLayer即可。这里可以看loss_layer.hpp的注释:

1
2
3
4

* This layer should be preferred over separate
* SoftmaxLayer + MultinomialLogisticLossLayer
* as its gradient computation is more numerically stable.
* At test time, this layer can be replaced simply by a SoftmaxLayer.

先看softmax_layer.cpp，由于只会用到他的forward，所以只看forward就好了。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

template <typename Dtype>
void SoftmaxLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
    vector<Blob<Dtype>*>* top) {
  const Dtype* bottom_data = bottom[0]->cpu_data();
  Dtype* top_data = (*top)[0]->mutable_cpu_data();
  Dtype* scale_data = scale_.mutable_cpu_data();
  int num = bottom[0]->num();
  int channels = bottom[0]->channels();
  int dim = bottom[0]->count() / bottom[0]->num();
  int spatial_dim = bottom[0]->height() * bottom[0]->width();
  caffe_copy(bottom[0]->count(), bottom_data, top_data);
  // We need to subtract the max to avoid numerical issues, compute the exp,
  // and then normalize.
  for (int i = 0; i < num; ++i) {
    // initialize scale_data to the first plane
    caffe_copy(spatial_dim, bottom_data + i * dim, scale_data);
    for (int j = 0; j < channels; j++) {
      for (int k = 0; k < spatial_dim; k++) {
        scale_data[k] = std::max(scale_data[k],
            bottom_data[i * dim + j * spatial_dim + k]);
      }
    }
    // subtraction
    caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels, spatial_dim,
        1, -1., sum_multiplier_.cpu_data(), scale_data, 1., top_data + i * dim);
    // exponentiation
    caffe_exp<Dtype>(dim, top_data + i * dim, top_data + i * dim);
    // sum after exp
    caffe_cpu_gemv<Dtype>(CblasTrans, channels, spatial_dim, 1.,
        top_data + i * dim, sum_multiplier_.cpu_data(), 0., scale_data);
    // division
    for (int j = 0; j < channels; j++) {
      caffe_div(spatial_dim, top_data + (*top)[0]->offset(i, j), scale_data,
          top_data + (*top)[0]->offset(i, j));
    }
  }
}

可以看出基本就是softmax的假设时候的实现公式，即这条。

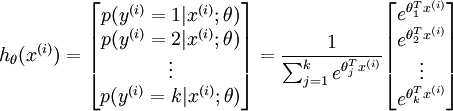
不同之处是先求取max然后所有值先减去了这个max，目的作者也给了注释是数值问题，毕竟之后是要接上e为底的指数运算的，所以值不可以太大，这个操作相当合理。

然后就到了softmax_loss_layer.cpp了，总共代码不超100行，就全贴在下面了:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

#include <algorithm>
#include <cfloat>
#include <vector>

#include "caffe/layer.hpp"
#include "caffe/util/math_functions.hpp"
#include "caffe/vision_layers.hpp"

namespace caffe {

template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::LayerSetUp(
    const vector<Blob<Dtype>*>& bottom, vector<Blob<Dtype>*>* top) {
  LossLayer<Dtype>::LayerSetUp(bottom, top);
  softmax_bottom_vec_.clear();
  softmax_bottom_vec_.push_back(bottom[0]);
  softmax_top_vec_.clear();
  softmax_top_vec_.push_back(&prob_);
  softmax_layer_->SetUp(softmax_bottom_vec_, &softmax_top_vec_);
}

template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::Reshape(
    const vector<Blob<Dtype>*>& bottom, vector<Blob<Dtype>*>* top) {
  LossLayer<Dtype>::Reshape(bottom, top);
  softmax_layer_->Reshape(softmax_bottom_vec_, &softmax_top_vec_);
  if (top->size() >= 2) {
    // softmax output
    (*top)[1]->ReshapeLike(*bottom[0]);
  }
}

template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::Forward_cpu(
    const vector<Blob<Dtype>*>& bottom, vector<Blob<Dtype>*>* top) {
  // The forward pass computes the softmax prob values.
  softmax_layer_->Forward(softmax_bottom_vec_, &softmax_top_vec_);
  const Dtype* prob_data = prob_.cpu_data();
  const Dtype* label = bottom[1]->cpu_data();
  int num = prob_.num();
  int dim = prob_.count() / num;
  int spatial_dim = prob_.height() * prob_.width();
  Dtype loss = 0;
  for (int i = 0; i < num; ++i) {
    for (int j = 0; j < spatial_dim; j++) {
      loss -= log(std::max(prob_data[i * dim +
          static_cast<int>(label[i * spatial_dim + j]) * spatial_dim + j],
                           Dtype(FLT_MIN)));
    }
  }
  (*top)[0]->mutable_cpu_data()[0] = loss / num / spatial_dim;
  if (top->size() == 2) {
    (*top)[1]->ShareData(prob_);
  }
}

template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
    const vector<bool>& propagate_down,
    vector<Blob<Dtype>*>* bottom) {
  if (propagate_down[1]) {
    LOG(FATAL) << this->type_name()
               << " Layer cannot backpropagate to label inputs.";
  }
  if (propagate_down[0]) {
    Dtype* bottom_diff = (*bottom)[0]->mutable_cpu_diff();
    const Dtype* prob_data = prob_.cpu_data();
    caffe_copy(prob_.count(), prob_data, bottom_diff);
    const Dtype* label = (*bottom)[1]->cpu_data();
    int num = prob_.num();
    int dim = prob_.count() / num;
    int spatial_dim = prob_.height() * prob_.width();
    for (int i = 0; i < num; ++i) {
      for (int j = 0; j < spatial_dim; ++j) {
        bottom_diff[i * dim + static_cast<int>(label[i * spatial_dim + j])
            * spatial_dim + j] -= 1;
      }
    }
    // Scale gradient
    const Dtype loss_weight = top[0]->cpu_diff()[0];
    caffe_scal(prob_.count(), loss_weight / num / spatial_dim, bottom_diff);
  }
}


#ifdef CPU_ONLY
STUB_GPU(SoftmaxWithLossLayer);
#endif

INSTANTIATE_CLASS(SoftmaxWithLossLayer);


}  // namespace caffe

其实这个函数挺好懂的，总结起来大致是：

  • 首先这里直接内置了一个SoftmaxLayer，利用它直接得到概率值prob_
  • 之后的forward和backward都很直观了，就是没有正则项的loss function和梯度的实现方式。（这里为啥没有考虑正则项，是因为正则项的代码不是写在这这里的，而是在更新梯度时候再一起考虑的，具体可以看layer的更新代码，会发现考虑了一个叫decay的东西）
  • 这里有了spatial_dim的概念后，就可以直接支持做全图的softmax了，具体来可以参考FCN一文中最后做20类分类的概率图的那个全图softmax

这篇关于Caffe源码阅读（3）Softmax层和SoftmaxLoss层的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1050235。

相关文章

JAVA智听未来一站式有声阅读平台听书系统小程序源码

JAVA智听未来一站式有声阅读平台听书系统小程序源码

智听未来，一站式有声阅读平台听书系统 🌟&nbsp;开篇：遇见未来，从“智听”开始 在这个快节奏的时代，你是否渴望在忙碌的间隙，找到一片属于自己的宁静角落？是否梦想着能随时随地，沉浸在知识的海洋，或是故事的奇幻世界里？今天，就让我带你一起探索“智听未来”——这一站式有声阅读平台听书系统，它正悄悄改变着我们的阅读方式，让未来触手可及！ 📚&nbsp;第一站：海量资源，应有尽有 走进“智听
阅读更多...
Java ArrayList扩容机制 （源码解读）

Java ArrayList扩容机制 （源码解读）

结论：初始长度为10，若所需长度小于1.5倍原长度，则按照1.5倍扩容。若不够用则按照所需长度扩容。 一. 明确类内部重要变量含义         1：数组默认长度         2:这是一个共享的空数组实例，用于明确创建长度为0时的ArrayList ，比如通过 new ArrayList<>(0)，ArrayList 内部的数组 elementData 会指向这个 EMPTY_EL
阅读更多...
如何在Visual Studio中调试.NET源码

如何在Visual Studio中调试.NET源码

今天偶然在看别人代码时，发现在他的代码里使用了Any判断List<T>是否为空。 我一般的做法是先判断是否为null，再判断Count。 看了一下Count的源码如下： 1 [__DynamicallyInvokable]2 public int Count3 {4 [__DynamicallyInvokable]5 get
阅读更多...
工厂ERP管理系统实现源码（JAVA）

工厂ERP管理系统实现源码（JAVA）

工厂进销存管理系统是一个集采购管理、仓库管理、生产管理和销售管理于一体的综合解决方案。该系统旨在帮助企业优化流程、提高效率、降低成本，并实时掌握各环节的运营状况。 在采购管理方面，系统能够处理采购订单、供应商管理和采购入库等流程，确保采购过程的透明和高效。仓库管理方面，实现库存的精准管理，包括入库、出库、盘点等操作，确保库存数据的准确性和实时性。 生产管理模块则涵盖了生产计划制定、物料需求计划、
阅读更多...
论文阅读笔记: Segment Anything

论文阅读笔记: Segment Anything

文章目录 Segment Anything摘要引言任务模型数据引擎数据集负责任的人工智能 Segment Anything Model图像编码器提示编码器mask解码器解决歧义损失和训练 Segment Anything 论文地址: https://arxiv.org/abs/2304.02643 代码地址:https://github.com/facebookresear
阅读更多...
Spring 源码解读：自定义实现Bean定义的注册与解析

Spring 源码解读：自定义实现Bean定义的注册与解析

引言 在Spring框架中，Bean的注册与解析是整个依赖注入流程的核心步骤。通过Bean定义，Spring容器知道如何创建、配置和管理每个Bean实例。本篇文章将通过实现一个简化版的Bean定义注册与解析机制，帮助你理解Spring框架背后的设计逻辑。我们还将对比Spring中的BeanDefinition和BeanDefinitionRegistry，以全面掌握Bean注册和解析的核心原理。
阅读更多...
音视频入门基础：WAV专题（10）——FFmpeg源码中计算WAV音频文件每个packet的pts、dts的实现

音视频入门基础：WAV专题（10）——FFmpeg源码中计算WAV音频文件每个packet的pts、dts的实现

一、引言 从文章《音视频入门基础：WAV专题（6）——通过FFprobe显示WAV音频文件每个数据包的信息》中我们可以知道，通过FFprobe命令可以打印WAV音频文件每个packet（也称为数据包或多媒体包）的信息，这些信息包含该packet的pts、dts： 打印出来的“pts”实际是AVPacket结构体中的成员变量pts，是以AVStream->time_base为单位的显
阅读更多...
kubelet组件的启动流程源码分析

kubelet组件的启动流程源码分析

概述 摘要: 本文将总结kubelet的作用以及原理，在有一定基础认识的前提下，通过阅读kubelet源码，对kubelet组件的启动流程进行分析。 正文 kubelet的作用 这里对kubelet的作用做一个简单总结。 节点管理 节点的注册 节点状态更新 容器管理(pod生命周期管理) 监听apiserver的容器事件 容器的创建、删除(CRI) 容器的网络的创建与删除
阅读更多...
软件架构模式：5 分钟阅读

软件架构模式：5 分钟阅读

原文： https://orkhanscience.medium.com/software-architecture-patterns-5-mins-read-e9e3c8eb47d2 软件架构模式：5 分钟阅读 当有人潜入软件工程世界时，有一天他需要学习软件架构模式的基础知识。当我刚接触编码时，我不知道从哪里获得简要介绍现有架构模式的资源，这样它就不会太详细和混乱，而是非常抽象和易
阅读更多...
red5-server源码

red5-server源码

red5-server源码：https://github.com/Red5/red5-server
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2