外部排序快速入门详解:基本原理，败者树，置换-选择排序，最佳归并树

本文主要是介绍外部排序快速入门详解:基本原理，败者树，置换-选择排序，最佳归并树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

外部排序

为什么要学习外部排序？
答：
在处理数据的过程中，我们需要把磁盘(外存）中存储的数据拿到内存中处理，因为内存处理更快，但是由于内存空间较小，外存空间很大，外存中的数据元素太多，无法一次全部读入内存进行排序。所以，通过外部排序就是实现对于外存存储元素排序的方法。

1.最基本的外部排序原理

假设在外存中，我们有48个记录，按照每三个记录为一块，建立好基本16个分块。
注意：在建立基本的分块之前，外存的每个小分块要先进行内部排序，保证这16个分块内部是有序的。
内存中，有2个输入缓冲区和1个输出缓冲区，采用归并排序的思想，第一次，先从16个分块中拿出两块，分别放入缓冲区1和缓冲区2.然后每次从这两个缓冲区6的开头，选最小的，放入输出缓冲区，然后凑齐3个记录，就回填外存。以此类推，直到把这1个分块，变为8个分块。

第二次开始，本质还是这个过程，但是值得注意的是，我们必须保证输入缓冲区不空，即如果一旦一个缓冲区的元素被拿空了，要立刻用该分块的其它元素补上。

外部排序时间开销=读写外存的时间+内部排序所需时间+内部归并所需时间

不难得知，采用多路归并可以减少归并趟数。

记结论：
生成初始片段r个，进行k路归并
则趟数S=⌈log_k^r⌉

2.外部排序的优化

2.1 败者树优化方法

败者树用来减少关键字的比较次数。

将各个归并段段开头加入到败者树的叶子结点，然后开始构造败者树，注意，中间结点记录的是，当前胜者是来自哪个归并端，在得到冠军来自3号归并端后，将3号归并段的叶子结点移除，将3号归并段新的结点补上，此时，不需要比较太多次，通过败者树向上比较，就可以得出新的冠军，以此类推。

效率分析：
对于k路归并，第一次构造败者树需要对比关键字k-1次，
有了败者树，选出最小元素，只需要对比⌈log₂^k⌉

2.2 置换-选择排序优化方法

让归并段更少，即让归并段更长。

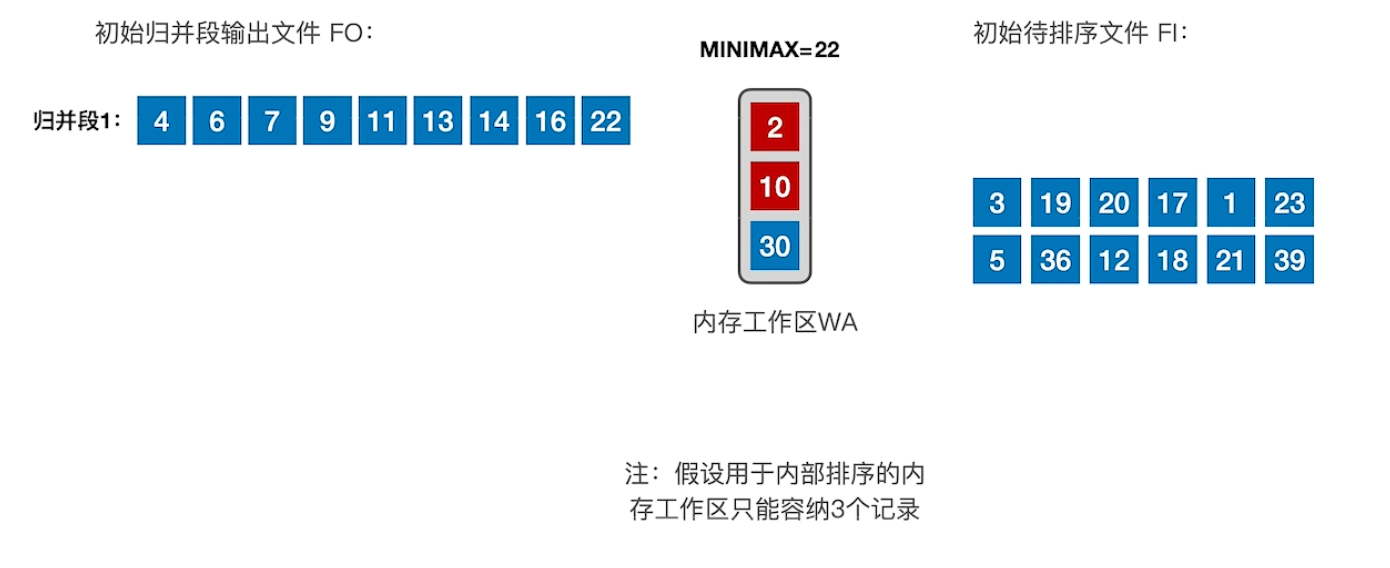
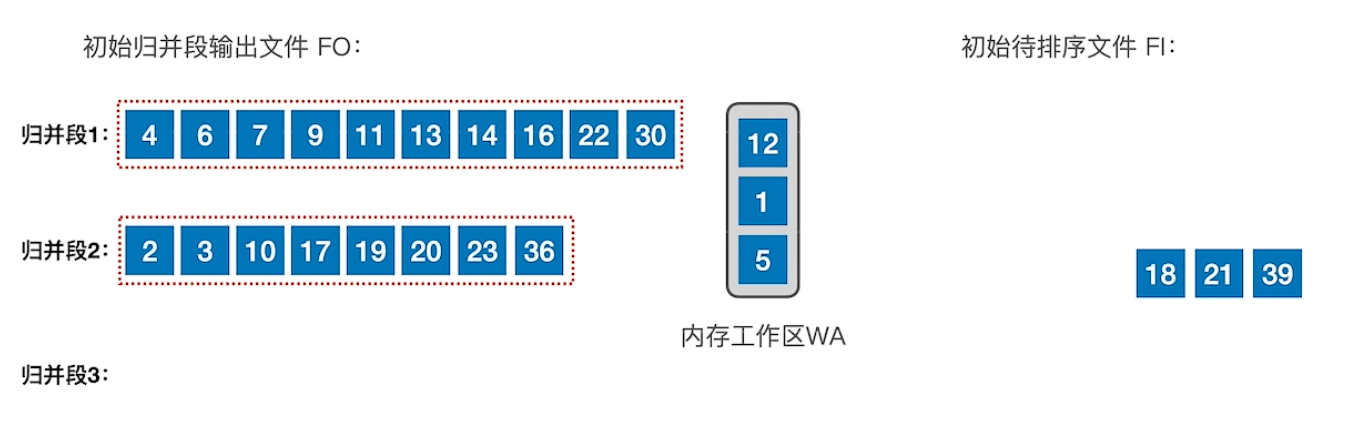
初始待排序文件，不断的将当前内存工作区中，大于minmax的最小值，加入归并段中，每加入一个，再从初始待排序文件中补充一个，直到内存工作区中的所有元素都小于minmax，然后开始输出归并段2，更改minmax，重复上述过程。

2.3 最佳归并树

对于归并过程进一步优化。

只讲干货：
每个初始归并端对应一个叶子结点，把归并段段块数作为叶子的权值。最好的归并的过程其实就是构造哈夫曼树的过程。
归并树的WPL=归并过程中的磁盘I/O次数

值得注意的是，k叉归并的最佳归并树一定是严格k叉树，所以很可能叶子结点的个数不满足构造严格k叉归并树，这时候需要补充虚段(权值为0的叶子结点，然后将这些权值为0的结点作为最初始的构造结点.

补充虚段的数量有公式：
（初始归并段数量-1)%（k-1）=u
若u=0,则说明不需要添加虚段，否则添加(k-1)-u个虚段。

下图是一个3路归并的最佳归并树。

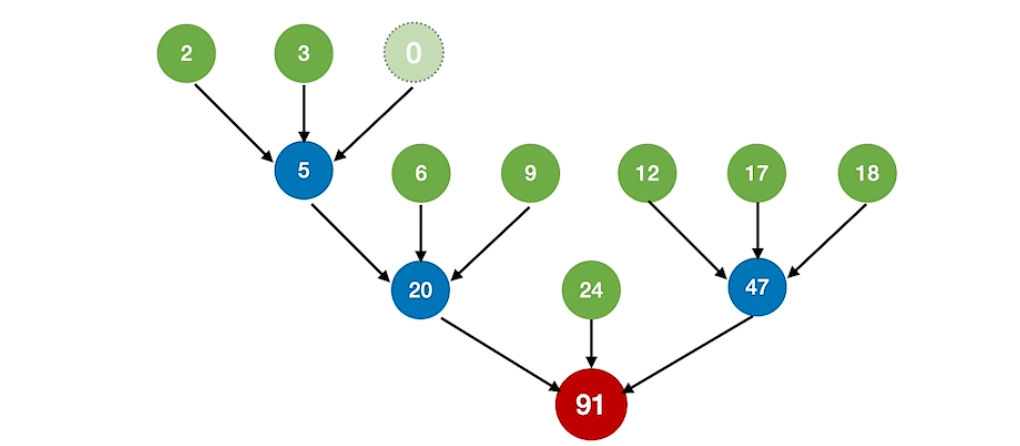
这篇关于外部排序快速入门详解:基本原理，败者树，置换-选择排序，最佳归并树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---