本文主要是介绍312. 戳气球 Hard,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。
示例 1:
输入:nums = [3,1,5,8]
输出:167
解释:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
示例 2:
输入:nums = [1,5]
输出:10
提示:
·n == nums.length
·1 <= n <= 300
·0 <= nums[i] <= 100
题目大意:在戳破一个气球可获得该气球与周围气球乘积数的情况下计算最多可获得的乘积数。
分析:
(1)在戳破一个气球后会造成不相邻的气球变得相邻,较难处理,因此考虑反向操作。将题目过程改为从两个数字为1的气球中不断插入气球,每次插入可获得插入球与相邻球的乘积数,计算最多可获得的乘积数;
(2)通过(1)中方法将问题转换为插入气球的问题,由于是从两个数字为1的气球开始插入,因此在nums数组的首尾插入数字1,再设dp[l][r]为在区间(l,r)中的气球全部插满最多可获得的硬币数。若区间(l,r)中第一个气球插入的位置为mid(l<mid<r),则dp[l][r]=dp[l][mid]+dp[mid][r]+nums[l]*nums[mid]*nums[r]。由此计算方式可得状态转移方程:
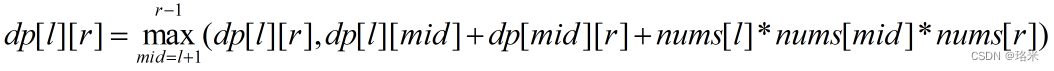
class Solution {
public:int maxCoins(vector<int>& nums) {nums.insert(nums.begin(),1);nums.emplace_back(1);int N=nums.size();vector<vector<int>> dp(N,vector<int>(N,0));for(int len=2,l,r,mid;len<N;++len){for(l=0,r=l+len;r<N;++l,++r){for(mid=l+1;mid<r;++mid){dp[l][r]=max(dp[l][r],dp[l][mid]+dp[mid][r]+nums[l]*nums[mid]*nums[r]);}}}return dp[0][N-1];}
};这篇关于312. 戳气球 Hard的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




