本文主要是介绍用例与用例之间的三种关系:泛化、包含、扩展,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
UML用例图(Use Case Diagrame),是UML图的一种,主要用来描述角色及角色与用例之间的连接关系。
1.泛化
当多个用例共有一种类似的结构和行为时。能够将他们的共性抽象成为父用例,其它的用例作为泛化关系的子用例。箭头指向父用例
用例图如
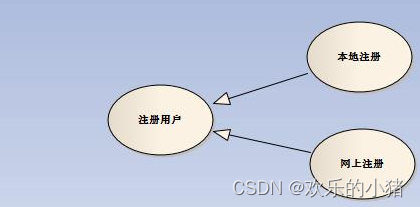
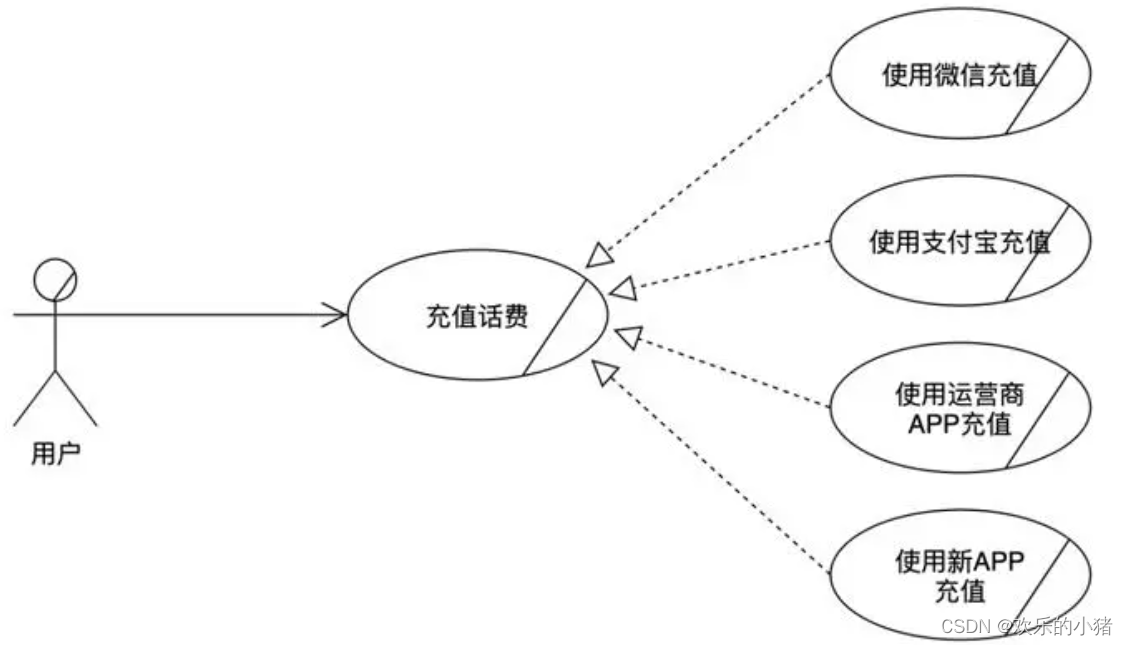
2.包含
当能够从两个或两个以上的用例中提取公共行为时,应该使用包含的关系来表示它们。这个提取出来的公共用例成为抽象用例。而把原始用例成为基本用例或基础用例。当中“<<include>>”是包括关系的构造型,箭头指向抽象用例。
用例图如
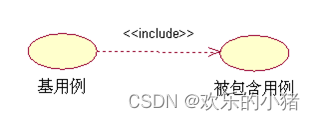

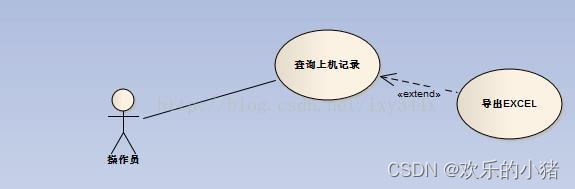
3.扩展
假设一个用例明显地混合了两种或者两种以上的不同场景,即依据情况可能发生多种分支,则能够将这个用例分为一个基本用例和一个或多个扩展用例。箭头指向基用例
用例图如
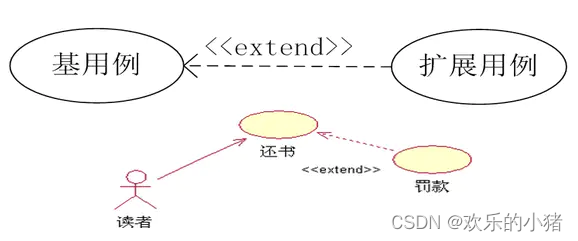
这篇关于用例与用例之间的三种关系:泛化、包含、扩展的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




