Q-function Q函数 （维基百科）

本文主要是介绍Q-function Q函数 （维基百科），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

如有翻译或者理解上的错误烦请指出

Q函数与正态分布的累积分布函数相关，并且是误差函数的补函数，这使得Q函数在应用数学和物理学中非常重要。

在统计学中，Q函数是标准正态分布的尾部分布函数[1][2]。换句话说，Q(x)是一个正态（高斯）随机变量取值大于x个标准差的概率。也可以理解为，Q(x)也是一个标准正态随机变量取值大于x的概率。

如果Y是一个均值μ和方差σ²的高斯随机变量，那么 $\frac{Y-\mu }{\sigma }$ 是标准正态分布的，
$$P(Y>y)=P(X>x)=Q(x)$$ 其中 $x=\frac{y-\mu }{\sigma }$。

Q函数的其他定义，也都是正态累积分布函数的简单变形，也经常使用[3]。

由于Q函数与正态分布的累积分布函数以及误差函数的关系，它在应用数学和物理学中扮演着重要的角色。

Q函数图像

定义和基本特性

Q函数的标准定义为：
$$Q(x)=\frac{1}{\sqrt{2\pi }}{\int }_x^{\infty }\exp \left(-\frac{u^2}{2}\right)du.$$
因此，
$$Q(x)=1-Q(-x)=1-\Phi (x),$$
其中 $\Phi (x)$是标准正态高斯分布的累积分布函数。

Q函数可以用误差函数或补误差函数来表达，如下：
$$\begin{array}{rl}Q(x)& =\frac{1}{2}\left(2{\int }_{\frac{x}{\sqrt{2}}}^{\infty }\exp (-t^2)dt\right)\\ & =\frac{1}{2}\left(1-\text{erf}\left(\frac{x}{\sqrt{2}}\right)\right)-\text{or}-\\ & =\frac{1}{2}\text{erfc}\left(\frac{x}{\sqrt{2}}\right).\end{array}$$
erf和erfc分别为误差函数和误差补函数。
已知的Q函数的另一种形式，称为Craig公式，由其发现者命名，表达如下[4]：
$$Q(x)=\frac{1}{\pi }{\int }_0^{\frac{\pi }{2}}\exp \left(-\frac{x^2}{2{\sin }^2\theta }\right)d\theta .$$
这个表达式仅对x的正值有效，但可以用 (Q(x) = 1 - Q(-x)) 来得到x的负值。这种形式的优点是积分范围是固定和有限的。

Craig公式后来被Behnad (2020)[5]扩展，用于两个非负变量之和的Q函数，如下：
$$Q(x+y)=\frac{1}{\pi }{\int }_0^{\frac{\pi }{2}}\exp \left(-\frac{x^2}{2{\sin }^2\theta }-\frac{y^2}{2{\cos }^2\theta }\right)d\theta ,x,y\ge 0.$$

复数域Q函数图像

边界和近似

• Q函数不是基本函数。但是它有上下界[6][7]：
  $$\frac{x}{1+x^2}\varphi (x)<Q(x)<\frac{\varphi (x)}{x},x>0,$$
  其中 $\varphi (x)$是标准正态分布的概率密度函数，这些界限随x增大而逐渐变得更加紧密。

• 通过替代$u=v\sqrt{2}$，上界可以推导如下：
  $$Q(x)={\int }_x^{\infty }\varphi (u)du<{\int }_x^{\infty }\frac{e^{-u^2/2}}{x\sqrt{2\pi }}du=\frac{e^{-x^2/2}}{x\sqrt{2\pi }}.$$
  类似地，使用${\varphi }^{\prime }(u)=-u\varphi (u)$和quotient rule，
  $$\left(1+\frac{1}{x^2}\right)Q(x)={\int }_x^{\infty }\left(1+\frac{1}{u^2}\right)\varphi (u)du>\left(1+\frac{1}{x^2}\right){\int }_x^{\infty }\frac{\varphi (u)}{u}du=\frac{\varphi (x)}{x}.$$

• Q(x)的解提供了下界。

• 上界和下界的几何平均给出了Q(x)的一个相对适合的近似：
  $$Q(x)\approx \frac{\varphi (x)}{\sqrt{1+x^2}},x\ge 0.$$

• 更紧的Q(x)的边界和近似也可以通过优化以下表达式获得[7]：
  $$\hat{Q}(x)=\frac{\varphi (x)}{(1-a)x+a\sqrt{x^2+b}}.$$
  例如，最佳上界是由 (a = 0.344) 和 (b = 5.334) 给出，最大绝对相对误差为0.44%。最佳下界是由 $a=1/\pi$和 $b=2\pi$给出，最大绝对相对误差为1.17%。

• Q函数的切诺夫界限是：
  $$Q(x)\le e^{-x^2/2},x>0.$$

• 改进的指数边界和纯粹的指数近似是[8]：
  $$Q(x)\le \frac{1}{4}{e}^{-x^2}+\frac{1}{2}{e}^{-x^2/2},x>0.$$
  $$Q(x)\approx \frac{1}{12}{e}^{-1.3x^2}+\frac{1}{4}{e}^{-0.3x^2},x>0.$$

• 以上由Tanash & Riihonen(2020)推广[9]，表明Q(x)可以被准确近似或界定。他们提出了一种系统的方法来解决数值系数 $\{(a_n,b_n){\}}_{n=1}^N$，使得 $Q(x)\approx \hat{Q}(x)$,$Q(x)\le \hat{Q}(x)$, 或 $Q(x)\ge \hat{Q}(x)$对于 $x\ge 0$。以N = 20为例，相对和绝对近似误差小于$2.831\times 10^{-6}$和 $1.416\times 10^{-6}$。针对指数函数的多种变体的系数 $\{(a_n,b_n){\}}_{n=1}^N$ 已经公开访问，作为一个全面的数据集[10]。

• 另一种近似 $Q(x)$ 对于 $x\in [0,\infty )$ 是由Karagiannidis和Lioumpas（2007）[11]提出的，他们展示了适当选择的参数 ({A, B}) 可以实现：
  $$f(x;A,B)=\frac{(1-e^{-Ax})e^{-x^2}}{B\sqrt{\pi x}}\approx \text{erfc}(x).$$
  在范围 $[0,R]$上，$f(x;A,B)$ 和 $\text{erfc}(x)$ 之间的绝对误差可以通过计算
  { A , B } = arg ⁡ min ⁡ { A , B } ∫ 0 R ∣ f ( x ; A , B ) − erfc ( x ) ∣ d x . \{A, B\} = \arg \min_{\{A,B\}} \int_0^R |f(x; A, B) - \text{erfc}(x)| \, dx. {A,B}=arg{A,B}min​∫0R​∣f(x;A,B)−erfc(x)∣dx.
  来最小化。使用 $R=20$ 并进行数值积分，他们找到了当 { A , B } = { 1.98 , 1.135 } \{A, B\} = \{1.98, 1.135\} {A,B}={1.98,1.135} 时，误差最小，这给出了 $\sqrt{x}\ge 0$ 的一个良好近似。带入这些值并利用上述 $\hat{Q}(x)$和 $\text{erfc}(x)$ 之间的关系可得：
  $$Q(x)\approx \frac{(1-e^{-1.98x})e^{-x^2/2}}{1.135\sqrt{2\pi x}},x\ge 0.$$
  对于上述“Karagiannidis-Lioumpas近似”，也可以使用替代系数，以便为特定应用专门定制精度或将其转换为紧密边界。[12]

• López-Benítez 和 Casadevall（2011）[13]基于二阶指数函数提出了更紧凑且可跟踪的$Q(x)$近似，适用于正值 $x\in [0,\infty )$：
  $$Q(x)\approx e^{-a{x}^2-bx-c},x\ge 0.$$
  这些系数 ((a, b, c)) 可以在任何所需的参数范围内进行优化，以最小化平方误差总和 ($a=0.3842,b=0.7640,c=0.6964$对于 $x\in [0,20]$) 或最小化最大绝对误差 ($a=0.4920,b=0.2887,c=1.1893$对于 $x\in [0,20]$)。这种近似提供了一个良好的折衷选择，并且可以在分析上扩展到任何 (Q(x)) 的幂次，而不改变近似的代数形式。

逆Q函数

逆Q函数可以与逆误差函数相关联：
$$Q^{-1}(y)=\sqrt{2}{\text{erf}}^{-1}(1-2y)=\sqrt{2}{\text{erfc}}^{-1}(2y).$$
这个函数在数字通信中有应用。通常用分贝（dB）表示，并通常称为Q因子：
$$Q\text{-factor}=20{\log }_{10}(Q^{-1}(y))\text{dB}$$
其中y是被分析的数字调制信号的误码率（BER）。例如，在加性白高斯噪声中的正交相移键控（QPSK）中，上述定义的Q因子恰好与信噪比的分贝值相对应，该信噪比产生等于y的误码率。

Q因子vs误码率

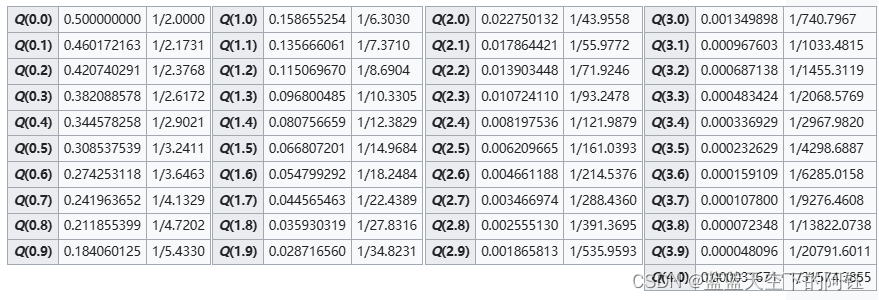
Q函数的值

q函数非常易于制作成表格，可以在大多数数学软件包中直接计算，如R和Python、MATLAB和Mathematica中提供的软件包。下面给出q函数的一些值，以供参考

高维度

Q函数可以推广到更高维度：
$$Q(\mathbf{x})=P(\mathbf{X}\ge \mathbf{x}),$$
其中 $\mathbf{X}\sim N(0,\Sigma )$ 遵循具有协方差矩阵 $\Sigma$的多元正态分布，且阈值的形式为$\mathbf{x}=\gamma {\mathbf{l}}^{\ast }$ ，这里 ${\mathbf{l}}^{\ast }>0$ 是一个正向量，$\gamma >0$是一个正常数。就像一维情况一样，没有简单的解析公式来表示多维的Q函数。然而，随着 $\gamma$ 的增加，Q函数可以被任意好地近似。

多一嘴 Marcum Q函数

MARCUM Q函数和标准Q函数（通常指的是高斯Q函数）在统计和通信理论中都有重要应用，但它们用于描述不同类型的概率分布和场景。讲讲两者主要区别和联系：

MARCUM Q函数

1. 定义：Marcum Q函数通常表示为 (Q_M(a, b))，它是一种特殊函数，常用于雷达信号处理和其他涉及非中心卡方分布的领域。该函数定义为：
   $$Q_M(a,b)={\int }_b^{\infty }x\exp \left(-\frac{x^2+a^2}{2}\right)I_{M-1}(ax)dx,$$
   其中$I_{M-1}(ax)$ 是第 $M-1$阶的修正贝塞尔函数，参数$a$和 $b$ 是非负实数，$M$是函数的阶。

2. 应用：Marcum Q函数广泛应用于雷达检测理论，特别是在评估非中心卡方分布的尾部概率时。

3. 特性：这个函数特别用于描述非中心参数下的随机变量的行为，与中心高斯分布的行为（由标凊Q函数描述）有所不同。

高斯Q函数

1. 定义：高斯Q函数定义为一个标准正态分布随机变量超过某个值的尾部概率。具体来说，它是：
   $$Q(x)=\frac{1}{\sqrt{2\pi }}{\int }_x^{\infty }\exp \left(-\frac{u^2}{2}\right)du,$$
   其中 $x$是任意实数。

2. 应用：高斯Q函数用于广泛的应用中，包括信号处理、通信理论中的误码率计算，以及其他需要评估高斯噪声影响的场合。

3. 特性：这个函数关注的是中心高斯随机变量的尾部行为，特别是在信号处理和统计分析中常见的场景。

区别和联系

• 应用领域的不同：高斯Q函数主要用于处理和分析高斯分布相关的问题，而Marcum Q函数更常见于处理有特定非中心参数的分布，如雷达和其他信号处理技术中的非中心卡方分布。
• 数学表达和复杂性：Marcum Q函数在数学形式上更复杂，包括修正贝塞尔函数，这使得它在分析和计算上比标准Q函数更为复杂。
• 共同点：两者都用于评估某种随机分布中超过某个阈值的概率，尽管它们适用的分布类型不同。

两种Q函数应用于不同类型的概率分布，并且有着不同的数学属性和应用领域。

参考文献

1. The Q-function, from cnx.org
2. Basic properties of the Q-function Archived March 25, 2009, at the Wayback Machine
3. Normal Distribution Function – from Wolfram MathWorld
4. Craig, J.W. (1991). “A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations”. MILCOM 91 - Conference record. pp. 571–575. doi:10.1109/MILCOM.1991.258319. ISBN 0-87942-691-8. S2CID 16034807.
5. Behnad, Aydin (2020). “A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis”. IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209.
6. Gordon, R.D. (1941). “Values of Mills’ ratio of area to bounding ordinate and of the normal probability integral for large values of the argument”. Ann. Math. Stat. 12: 364–366
7. Borjesson, P.; Sundberg, C.-E. (1979). “Simple Approximations of the Error Function Q(x) for Communications Applications”. IEEE Transactions on Communications. 27 (3): 639–643. doi:10.1109/TCOM.1979.1094433.
8. Chiani, M.; Dardari, D.; Simon, M.K. (2003). “New exponential bounds and approximations for the computation of error probability in fading channels” . IEEE Transactions on Wireless Communications. 24 (5): 840–845. doi:10.1109/TWC.2003.814350.
9. Tanash, I.M.; Riihonen, T. (2020). “Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials”. IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
10. Tanash, I.M.; Riihonen, T. (2020). “Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]”. Zenodo. doi:10.5281/zenodo.4112978.
11. Karagiannidis, George; Lioumpas, Athanasios (2007). “An Improved Approximation for the Gaussian Q-Function” . IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
12. Tanash, I.M.; Riihonen, T. (2021). “Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function”. IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
13. Lopez-Benitez, Miguel; Casadevall, Fernando (2011). “Versatile, Accurate, and Analytically Tractable Approximation for the Gaussian Q-Function” . IEEE Transactions on Communications. 59 (4): 917–922. doi:10.1109/TCOMM.2011.012711.100105. S2CID 1145101.
14. Savage, I. R. (1962). “Mills ratio for multivariate normal distributions”. Journal of Research of the National Bureau of Standards Section B. 66 (3): 93–96. doi:10.6028/jres.066B.011. Zbl 0105.12601.
15. Botev, Z. I. (2016). “The normal law under linear restrictions: simulation and estimation via minimax tilting”. Journal of the Royal Statistical Society, Series B. 79: 125–148. arXiv:1603.04166. Bibcode:2016arXiv160304166B. doi:10.1111/rssb.12162. S2CID 88515228.
16. Botev, Z. I.; Mackinlay, D.; Chen, Y.-L. (2017). “Logarithmically efficient estimation of the tail of the multivariate normal distribution”. 2017 Winter Simulation Conference (WSC). IEEE. pp. 1903–191. doi:10.1109/WSC.2017.8247926. ISBN 978-1-5386-3428-8. S2CID 4626481.

这篇关于Q-function Q函数 （维基百科）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---