本文主要是介绍多目标优化-NSGA-II,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、前置知识
- NSGA-II
- 帕累托前沿
- 二、算法流程
- 1.NSGA
- 2.NSGA-II
一、前置知识
1.NSGA(非支配排序遗传算法):旨在同时优化多个冲突的目标函数,寻找帕累托前沿上的解集。
什么是多个冲突的目标: 比如你看上了一辆车,你既想要它便宜,又想要它的配置达到Top水平,那这两个目标就是相互冲突的。
NSGA-II
NSGA-II其实就是NSGA算法的改进,缩减了算法的时间复杂度,其中NS是非支配排序,GA是遗传算法。
帕累托前沿
- 支配关系:
通俗来说就是A的能力比B强则A就能支配B。
满足两个条件:
(1)X的解不比Y差 (2)X解中至少有一个解比Y好,如果满足这两个条件,那说明X可以支配Y。
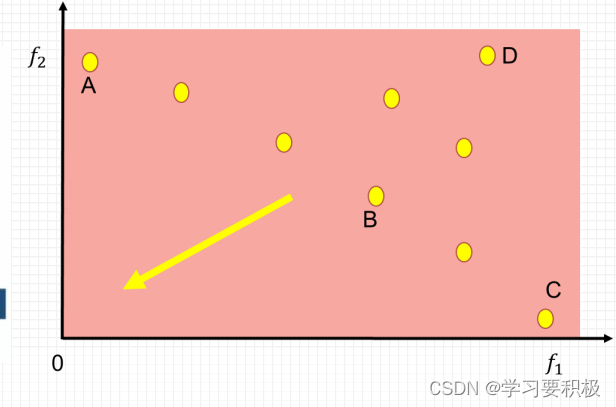
- 如上图(默认函数值越小越好):A可以支配D,B可以支配D,A和B相互无法支配
这些相互无法支配的解构成了非支配解(帕累托解)。
这些非支配解组成的集合称之为 帕累托最优集 ,这些解在目标空间中形成了 帕累托前沿。
-
帕累托前沿(Pareto Front) 是多目标优化问题中的一个关键概念,它是 帕累托最优解集(Pareto Optimal Set) 在目标空间中的表示。帕累托前沿是目标空间中所有帕累托解的集合,它展示了不同目标之间的最佳权衡。
-
对于这些非支配解和其右上方的解很容易进行比较,但是这些非支配解之间如何比较?我们引入了一个新的标准-拥挤距离

拥挤度较高的解(即周围解较为稀疏,远离其他解)会被认为更优。这有助于保持解集的多样性和均匀性,避免解决方案集中在帕累托前沿的某些区域。
二、算法流程
1.NSGA
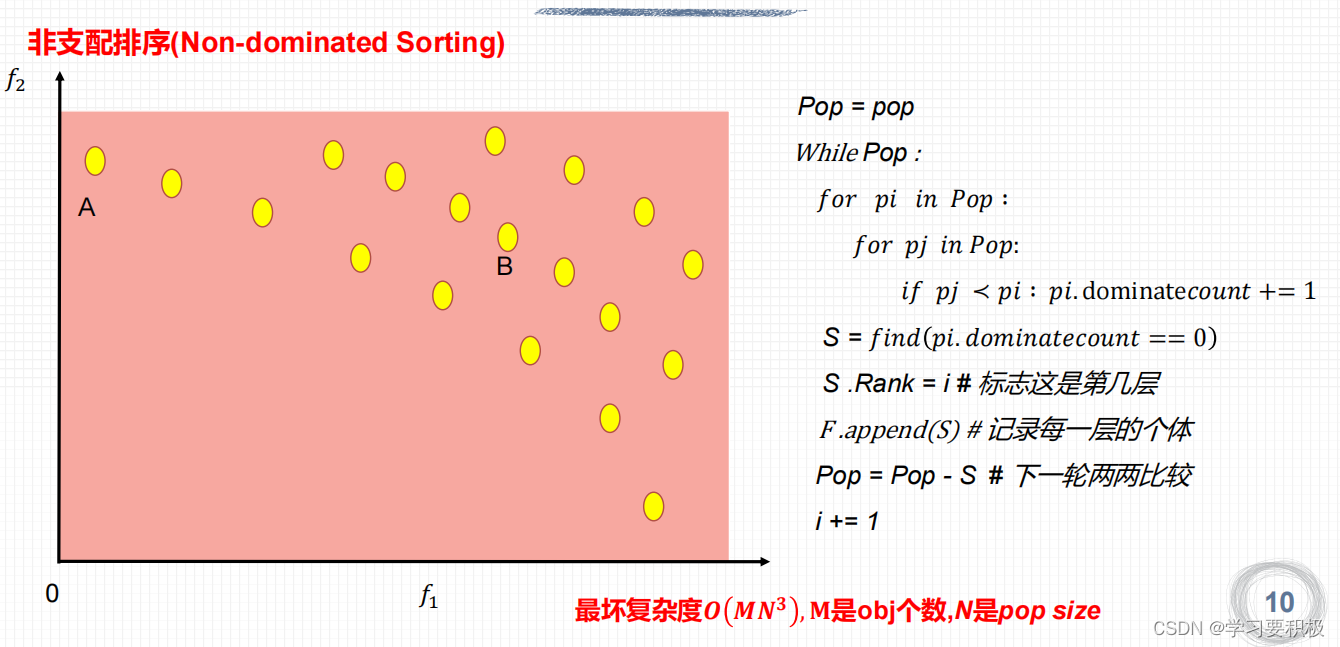
也就是对于种群中的每个个体,如图中的A依次会和剩余的所有个体进行比较,如果A被其它个体支配,则A被支配数加1,等每个个体的dominatecount被统计后就查找被支配数为0的个体并列为第一层,并记录下来,随后pop去掉这一层的个体,dominatecount清零后继续寻找第二层。一直等pop为0结束。
2.NSGA-II
在NSGA上进行改进,降低了时间复杂度。

这篇关于多目标优化-NSGA-II的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







