颠沛流离学二叉树(完结撒花篇)

本文主要是介绍颠沛流离学二叉树(完结撒花篇)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本篇会加入个人的所谓鱼式疯言

❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言

而是理解过并总结出来通俗易懂的大白话,

小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的.

🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人能接受我们这个概念 ！！！

前言

在上两篇 二叉树系列 的文章中，我们学习了二叉树的 概念，特性，遍历方式 ， 而在本篇文章中，将展开对 二叉树其他基本核心操作 的详解 ❤️ ❤️ ❤️ ❤️

提前透露一下哦， 本篇文章的基本操作，小编都会带着大家用 递归 和 非递归 的代码带着大家走一遍哦 💖 💖 💖 💖

目录

1. 获取树中节点的个数

2. 获取叶子节点的个数

3. 获取第 K 层的节点的个数

4. 获取二叉树的高度（最大深度）

5. 查找 节点的值等于的 value 的节点

6. 判断一棵树是否是完全二叉树

一. 获取树中节点的个数

1. 操作分析

由于我们的二叉树是分为 两边的，分别是 左子树 和 右子树 ， 要求树中的节点，我们就需要知道 左子树的节点 和 右子树的节点 ，最后加上自身的 1个根节点

2. 代码实现

<1>. 递归实现

// 递归计算节点个数
public int Size(TreeNode root) {if (root==null) {return 0;}return Size(root.left)+1+Size(root.right);
}

递归的代码实现，就是咱们 动画上的执行过程 了，小编在这里就不赘述了 💞 💞 💞 💞

动画展示

<2>. 非递归实现

// 非递归遍历节点个数public int nodeSize;public void setNodeSize(TreeNode root) {if (root==null) {return;}// 只要遍历过的节点// 就让 节点数 ++nodeSize++;// 先遍历左子树setNodeSize(root.left);// 遍历右子树setNodeSize(root.right);}

非递归的执行过程 :

我们这里利用了 前序遍历 的思路, 当我们每走过一个节点,就让我们的 nodeSize++

当完全的走过 每一个节点 , 我们 的 nodeSize 就加多少次

当我们遍历完 整个二叉树 , 也就统计出二叉树 所有的节点

鱼式疯言

关于求树中接节点个数的操作，小编最大的体会就是 子问题 的 递归思路

由于我们 递归 的是不断把 每一个节点重新看成是根节点 的思路

所以我们只需要求出每个根节点的个数。所累积的个数，不就是我们的 节点总数 吗 ！ ！ ！

这就是 子问题 的思路, 小伙伴在思考这一类问题时，一定要学会把一个 大问题 拆分成我们能解决的 一个一个小问题 的思想.

二. 获取叶子节点的个数

1. 操作分析

小伙伴都知道我们 二叉树的叶子节点 的定义，就是 度为0 的节点

那么我们该怎么找 度为零 的节点呢 💞 💞 💞 💞

其实很简单，我们只需要返回 左右子树 的 所有节点 同时 左节点 和 右子树 也为 null

最后 左右子树的叶子节点相加 即可

2. 代码实现

<1>. 递归实现

// 递归计算叶子个数
public int leafSize(TreeNode root) {if (root==null) {return 0;}if (root.left==null && root.right==null) {return 1;}return leafSize(root.left)+leafSize(root.right);
}

关于 递归实现 的执行步骤，下面就让小编用 动画 的形式来描述吧 😊 😊 😊 😊

动画展示

<2>. 非递归实现

public int leafSize;// 非递归求叶子节点的个数public void setLeafSize(TreeNode root) {if (root==null) {return;}// 如果左右节点为 null// 就是我们需要的节点if (root.right==null && root.left==null) {leafSize++;}// 遍历左子树setLeafSize(root.left);// 遍历右子树setLeafSize(root.right);}

非递归的实现过程：

非递归的根本是依赖于 我们的遍历 来实现的，当遍历到某个 左节点为 null 并且 右节点也为 null 时， 就令 leafSize ++

当遍历完整个 二叉树的所有节点，也就意味着 所有的叶子节点 已经被 leafSize 统计完了

鱼式疯言

对于 递归实现 的思路来说，我们还是用 子问题 的思路，把一棵树拆成 多颗子树

子树 又成为 新的树, 在新的树里面去寻找 左右子树都为null 的节点 ，

最终回归到 最开始的整棵树 上解决该问题 ！ ！ ！

三. 获取第 K 层的节点的个数

1. 操作分析

要得到 第 K 层的节点 ， 不免想起我们上一篇文章中所用的 层序遍历 的思想， 每一层也就相当于 二维数组中的每一行

所有要得到 每一层的节点数 ，本质上就是当我们 递归往下递的每走一行的 左子树和右子树 ， k 就 减去一行 。

最终 当 K = 1 时， 就回退到 整棵树的根节点 ，就是我们要 获取到 第 K 层的节点个数

2. 代码实现

 // 求树某深度的节点数public int treeIndexlength(TreeNode root , int key) {// 如果节点为 null 返回 0if (root==null) {return 0;}/**** 当 k = 1 时 就意味着到底最后一层* 返回当前根节点即可****/// 如果 这个位置 没有左右if (key==1) {return 1;}/*** 先统计左边的节点** 再统计右边的节点** 最后都要减少 key 次* 代表统计了一层** 也就是说每统计一层 ，就减少一层**///int left = treeIndexlength(root.left,key-1);// 再统计右边的节点int right = treeIndexlength(root.right,key-1);// 一直返回该 key 位置的节点return left+right;}

具体 递归的过程 我们通过下面动画展示：

鱼式疯言

扩展一下 ：

小伙伴有没有想到一个点：

   // 一直返回该 key 位置的节点return left+right;

我们这边是 直接返回 left + right 是得到我们当前 第k层 深度的节点数

但如果我们

 return left+right + 1;  

我们如果是 + 1 呢？

答案就是返回 从整棵树的根节点 到 第k层 的 所有节点总和

感兴趣的小伙伴可以自己 研究 哦, 小编在这里就不细讲了 💖 💖 💖 💖**（代码如下）**

// 求树某深度的到根节点所有节点数
public int treeIndexSize(TreeNode root , int key) {if (root==null) {return 0;}if (key==1) {return 1;}int left=treeIndexSize(root.left,key-1);int right=treeIndexSize(root.right,key-1);// key 位置开始查找节点 并 一直累加return left+right+1;
}

四.获取树的高度（最大深度）

1. 操作分析

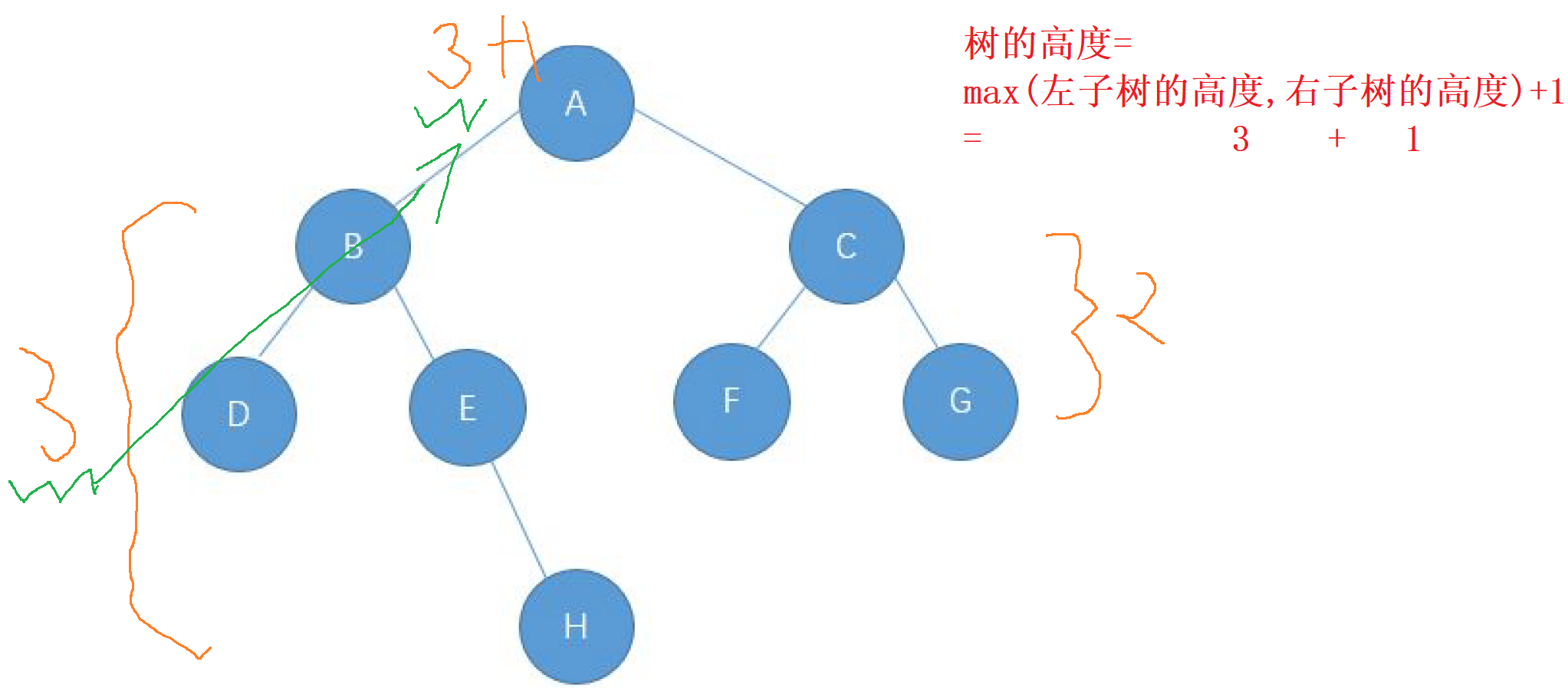
要获取高度小伙伴们先得理解高度该怎么来， 我们可以设想一下，

如果一颗树的左子树高度为 3 右子树的高度为 4 ， 那么 这颗树的高度是 3 还是 4 ，

很显然 这都 不对

树的高度最终应该是 5 才对， 因为啊， 我们树的高度是 左右子树中较高的那个高度 再 + 上自身根节点的高度 1 ， 所以我们得到的树的高度是 4 + 1 才对

2. 代码实现

// 返回树的最大深度
public int treeHeight(TreeNode root) {if (root==null) {return 0;}// 求左子树的深度int leftnum=treeHeight(root.left);// 求右子树的深度int rightnum=treeHeight(root.right);/*** 根据左右子树两边的高度** 哪边高 取 哪边*  最后还要加上该节点的高度**/return leftnum>rightnum? leftnum+1: rightnum+1;
}

具体我们由于递归不好描述，请小伙伴们看动画分析递归的全过程哦 💫 💫 💫 💫

动画展示

鱼式疯言

当我们用 子问题 的思路 在 寻找数的高度 的关键在于我们要注意加上不仅要比较 两端左子树和右子树 的 高度， 那个自身的 根节点的 1 也要同时加上

五. 查找节点的值等于的 value 的节点

1. 操作分析

查找某个等于 val 的值， 我们就需要在 遍历的基础上 完成

所以我们只需要考虑 一点 即可，当我们在遍历过程中

如果 左子树或者右子树 的节点的 val 找到了等于 val 就返回该 节点 ， 如果没找到就返回 null .

2. 代码实现

// 查找节点public TreeNode find(TreeNode root, char val) {if(root==null) {return null;}// 判断新的根节点的 val 是否 等于目标值 valif (Character.compare(val,root.val)==0) {return  root;}// 在左子树中查找该节点TreeNode node1=  find(root.left,val);// 一旦找到就返回该节点if (node1 !=null) {return node1;}// 在右子树中查找该今节点TreeNode node2= find(root.right,val);// 一点找到就返回该节点if (node2 !=null) {return node2;}// 都没有找到就返回 nullreturn  null;}

下面我们看看动画对于这段代码的理解吧 🤔 🤔 🤔 🤔

动画展示

鱼式疯言

细节处理：

   // 在左子树中查找该节点TreeNode node1=  find(root.left,val);// 一旦找到就返回该节点if (node1 !=null) {return node1;}// 在右子树中查找该今节点TreeNode node2= find(root.right,val);// 一点找到就返回该节点if (node2 !=null) {return node2;}

我想肯定有小伙伴会直接返回 node1 或者 node2 的值， 而不加判断， 这样做是不是有点问题呢 ？？？

是的，是有些问题，小伙伴应该知道如果我们先 递归左子树 或者 右子树 来达到遍历的效果， 一但 左子树没有找到该 val 的 目标值 ，就会去右边的 右子树 找

p但我们 中途一旦返回，就会陷入只找寻 左边一个节点 ，然后就直接返回了，未达到遍历的效果 , 也就更不可能找到我们的 val 值了

六. 判断一棵树是否是完全二叉树

1. 操作分析

要考虑是否是完全二叉树，我们只需要考虑一点即可：

当 左子树 < 右子树高度 ： 用 -1 来标记，代表 不是完全二叉树

当 左子树 >= 右子树高度： 就返回该高度。

2. 代码实现

/*** 检查左子树和右子树的高度关系* * 当左子树 > 右子树时 ，就不是完全二叉树* 否则就是完全二叉树* @param root 根节点* @return 返回布尔类型* */private int CheckTreeCount(TreeNode root) {if (root==null) {return  0;}int left=CheckTreeCount(root.left);/*** 当此树不是完全二叉树的就返回 负数* * 而这里的判断是为了连接上一个递归下来的根节点* */// 当左子树不是完全二叉树时，就返回 -1 if (left < 0) {return -1;}int right=CheckTreeCount(root.right);// 当右子树不是完全二叉树时， 就返回 -1 if(right < 0) {return  -1;}// 当左子树的高度 < 右子树的高度// 就说明不是完全二叉树if (left < right) {return -1;} else {// 该节点是完全二叉树时，就返回当前高度return Math.max(left,right)+1;}}

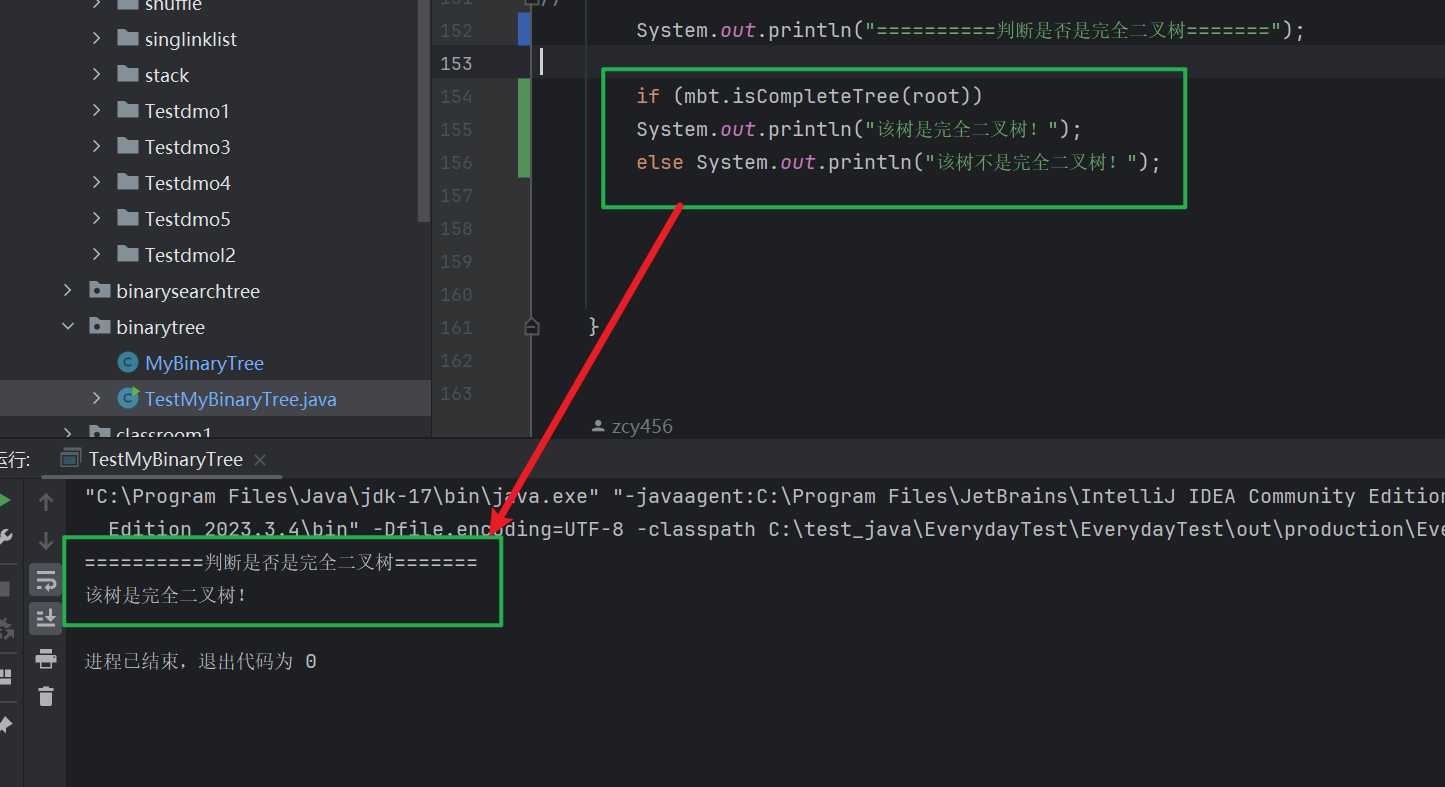
具体实现，请小伙伴们观看下面动态理解哦 ❣️ ❣️ ❣️ ❣️

鱼式疯言

int left=CheckTreeCount(root.left);/*** 当此树不是完全二叉树的就返回 负数* * 而这里的判断是为了连接上一个递归下来的根节点* */// 当左子树不是完全二叉树时，就返回 -1 if (left < 0) {return -1;}int right=CheckTreeCount(root.right);// 当右子树不是完全二叉树时， 就返回 -1 if(right < 0) {return  -1;}

细节处理：

这里有小伙伴就问了，我可以把

   if (left < 0) {return -1;}

和

if(right < 0) {return  -1;}

去掉吗？

答案是 不行 的

因为当我们一旦判断出 有一颗子树 的 左子树的高度 > 右子树的高度 时 ， 就必须返回 -1 ，然后就必须回退到上一个 根节点中

如果没有及时返回 -1 ，就有可能造成 max（-1，-1） 的情况，这种情况是 不可预料 的，所以我们呢需要 及时返回

总结

1. 获取树中节点的个数： 我们通过都用了 子问题 和 遍历 的获取节点的个数，但子问题要 注意的是需要加上自身的那个 节点数的 1

2. 获取叶子节点的个数 : 获取叶子节点，我们主要是根据它自身的特点 （左右节点是否同时为 null ） ,成立时我们就返回 当前节点 .

3. 获取第 K 层的节点的个数 : 获取 第K层的节点数 的思路在遍历的情况下，每走一层，k就减去1 , 当 k= 1 时就到达该层，返回 该层节点数 即可

4. 获取二叉树的高度（最大深度）：求树的高度，本质是抓住我们左子树和右子树的 较高 的那个高度，然后 加上 自身的高度1 即可

5. 查找 节点的值等于的 value 的节点 ：查找 val 是在遍历的情况下完成的，只需要在 边遍历边查找 ，一旦找到就返回该节点即可

6. 判断一棵树是否是完全二叉树 ： 完全二叉树的判断是建立在获取二叉树高度的思路上进行变通的， 根据完全二叉树成立条件： 左子树 >= 右子树 ，这个特点来判断即可

如果觉得小编写的还不错的咱可支持 三连 下 (定有回访哦) , 不妥当的咱请评论区 指正

希望我的文章能给各位宝子们带来哪怕一点点的收获就是 小编创作 的最大 动力 💖 💖 💖

这篇关于颠沛流离学二叉树(完结撒花篇)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---