判断两个矩形是否有重合部分

本文主要是介绍判断两个矩形是否有重合部分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最近在做人工智能项目，需要对两个矩形是否有重合做出判读

但注意的是，不是判断两个检测目标是否重合，检测目标的矩形只要左上角点和右下角点就可表示一个矩形，判断是否重合比较简单，但是现在是两个矩形是有一定旋转角度的，旋转角度不定，这样就没法像检测目标那样判断了。

目前使用四个点坐标表示一个矩形

判断分两个步骤：

一、当一个矩形的顶点在另一矩形内时，则可以判断两个矩形有重合。当这种情况不存在时，不能判断两个矩形不重合，需要借助其他方法判断。

判断矩形任意一顶点是否在另一矩形内，这样就需要利用点在多边形内的判断方法

可以参考博客https://blog.csdn.net/gf771115/article/details/42870605/，这篇博客对原理做了较为详细的讲解，并且提供了判断函数的不同演进形式。

int pnploy(const int poly_sides, const float *poly_X, const float *poly_Y, const float x, const float y)
{
int i, j;
j = poly_sides - 1;
int res = 0;
for (i = 0; i<poly_sides; i++)
{
if ((poly_Y[i]<y && poly_Y[j] >= y || poly_Y[j]<y && poly_Y[i] >= y) && (poly_X[i] <= x || poly_X[j] <= x))
{
res ^= ((poly_X[i] + (y - poly_Y[i]) / (poly_Y[j] - poly_Y[i])*(poly_X[j] - poly_X[i])) < x);
}
j = i;
}
return res;
}

该判断方法又叫射线法，由点向任何一个方向引出射线，与多边形交点数为奇数的，则点在多边形内，为偶数时，则点不在多边形内，为了简化这种判断过程，通常C++代码中使用水平射线来做计算。

二、当任一矩形的任何顶点都不在另一矩形内时，是不能判断两个矩形不重合的，因为还有一些特殊情况

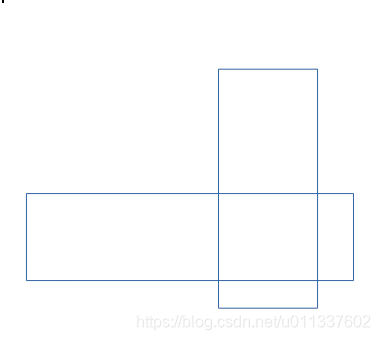
特例如下,以下情况就是顶点不在另一个矩形内，但是矩形重合的。

这样就需要利用矩形边交叉来判断重合，通常矩形边交叉，则相互重合的。

这样就需要判断两条线段是否交叉，

https://www.cnblogs.com/wuwangchuxin0924/p/6218494.html 该博客为我提供了方法

判断线段交叉两个步骤，(1)快速排斥 (2)跨立实验，具体请参考我上面提供的链接
bool linecross(const Point a, const Point b, const Point c,const Point d)
{
//快速排斥
if(!(std::min(a.x,b.x)<=std::max(c.x,d.x)
&& std::min(c.x,d.x)<= std::max(a.x,b.x)
&& std::min(a.y,b.y)<= std::max(c.y,d.y)
&& std::min(c.y,d.y)<= std::max(a.y,b.y)))
return false;
//跨立实验
double u,v,w,z;
u=(c.x-a.x)*(b.y-a.y)-(b.x-a.x)*(c.y-a.y); //AC×AB
v=(d.x-a.x)*(b.y-a.y)-(b.x-a.x)*(d.y-a.y); //AD×AB
w=(a.x-c.x)*(d.y-c.y)-(d.x-c.x)*(a.y-c.y); //CA×AB
z=(b.x-c.x)*(d.y-c.y)-(d.x-c.x)*(b.y-c.y); //CB×AB

if(u*v<=1e-9&&w*z<=1e-9)
return true;
return false;
}

好，这样我们就可以基于以上提供的方法，做出两个矩形是否会重合的判断逻辑了，目前可以试用于四边形，没测试过其他形状。大家如果觉得判断有问题或者一些效率上的问题，欢迎提出。
//目前只支持4边形交互
bool checkployintersect(const Point ploy1[4], const Point ploy2[4])
{
   Polygon polygon1, polygon2;
   for(int i = 0; i< 4; i++)
   {
       polygon1.x[i]=ploy1[i].x;
       polygon1.y[i]=ploy1[i].y;
       polygon2.x[i]=ploy2[i].x;
   polygon2.y[i]=ploy2[i].y;
   }

   for(int i =0; i<4; i++)
   {
       if(pnploy(4,polygon1.x,polygon1.y, polygon2.x[i], polygon2.y[i]))
       {
           return true;
       }
       if(pnploy(4,polygon2.x,polygon2.y, polygon1.x[i], polygon1.y[i]))
       {
           return true;
       }
   }
   for(int i=0; i<4; i++)
   {
       for(int j=0; j<4; j++)
       {
           if(linecross(ploy1[i%4], ploy1[(i+1)%4], ploy2[j%4], ploy2[(j+1)%4]))
           {
               return true;
           }
       }
   }
   return false;
}